基于改良BP神经网络的生物质锅炉飞灰含碳量预测模型研究

朱琎琦，牛晓凡，肖显斌

（华北电力大学 生物质发电成套设备国家工程实验室，北京 102206）

0 前言

生物质发电具有环保和普惠民生的天然属性，在大气污染治理、乡村振兴、解决“三农”问题、精准扶贫、城镇化建设、节能减排、绿色能源推广等方面发挥了重要作用，具有显著的社会效益和环境效益。 近年来，我国的生物质发电装机容量由 2003 年的150 万 kW 发展到2017 年的近1 500 万 kW[1]。

飞灰含碳量是与锅炉燃烧效率有关的一项重要参数，生物质锅炉的飞灰含碳量一般都在10%以上，尤其是燃用树皮和板皮的生物质锅炉，飞灰含碳量可达15%以上，导致生物质锅炉的燃烧效率下降[2]。 因此，需要在准确测量飞灰含碳量的基础上，建立一个飞灰含碳量的预测模型来研究各因素对飞灰含碳量的影响特性，从而提高锅炉燃烧效率，最终指导锅炉运行优化[3]。 目前，飞灰含碳量的主要测量方法是灼烧失重法，该方法具有测量精度高，不受燃料影响的优点[4]。 在此基础上，飞灰含碳量软测量法的基本思想是通过机理分析确定影响飞灰含碳量的因素，然后基于人工智能方法建立这些因素与飞灰含碳量的关系，得到一个预测模型。 它可以准确地预测燃煤锅炉在不同工况下的飞灰含碳量，从而为电厂提高锅炉效率提供依据。因此，飞灰含碳量软测量法得到了许多学者的关注[5]～[10]。 崔锐提出了一种基于LM算法优化BP 神经网络的飞灰含碳量预测方法，并通过仿真实验证明了该方法对飞灰含碳量的预测比较准确[5]。 但是，锅炉的燃烧过程是一个多变量、非线性、强耦合的热工过程，影响飞灰含碳量的众多因素间具有非线性相关性，这些相关性会造成输入信息的冗余，从而降低模型预测能力并增加计算复杂度，因此，有必要通过变量选择来消除冗余信息[6]。冯旭刚采用基于遗传神经网络的飞灰含碳量测量方法，对连接权值、阈值和隐层节点个数进行了优化计算，提高了神经网络的泛化能力[7]。 刘苹稷建立了利用主元分析优化的BP 神经网络飞灰含碳量预测模型，通过对输入进行降维，使模型更加精确可靠[8]。

除此之外，对BP 神经网络进行降维的方法还有多种，如基于敏感性分析的Garson 算法，但是，Garson 算法还未被应用于生物质锅炉的飞灰含碳量预测领域[11]。 因此，本文针对生物质锅炉的飞灰含碳量建立了一个基于LM 算法的BP 神经网络模型，分别通过主成分分析法和Garson 算法对模型进行降维优化，并比较两种优化方法的优劣之处。

1 BP神经网络

1.1 基本算法

BP（Back Propagation）神经网络是应用最广泛的多层前向网络，由“信号的正向传递”和“误差的反向传播”两个过程组成，重复这两个过程至满足精度要求时，模型建立完毕。 BP 神经网络的基本结构如图1 所示[12]。

图1 BP 神经网络模型基本结构Fig.1 Basic structure of BP neural network model

图1 中：ωml为输入层的第m 个神经元到隐含层的第l 个神经元之间的连接权值；wlj为隐含层第l 个神经元到输出层第j 个神经元之间的连接权值；yj为输出层第j 个神经元的实际输出。也可用θl和θj分别表示隐含层第l 个神经元和输出层第j 个神经元的阈值；νl表示隐含层第l 个神经元的输出，它将被传递到输出层神经元作为输入的一部分。

激励函数f 为Sigmoid 函数。

式中：c 为倾斜参数。

Sigmoid 函数的特点：对应幅值区间为（0，1），函数呈非线性递增光滑变化，但是，当输入u→+∞（或-∞）时，函数一致逼近于幅值 1（或 0）。Sigmoid 函数的基本算法如下。

（1）信号的正向传递

隐含层中第l 个神经元的输出为

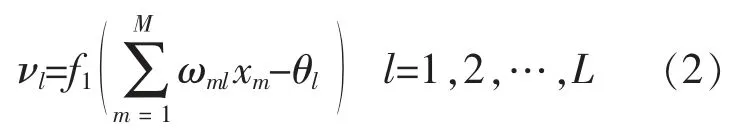
输出层中第j 个神经元的输出为

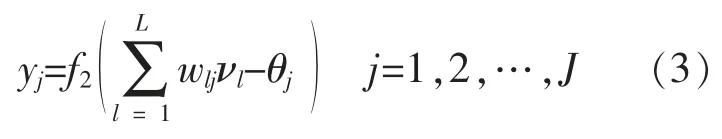
第i 个样本的神经网络学习误差为

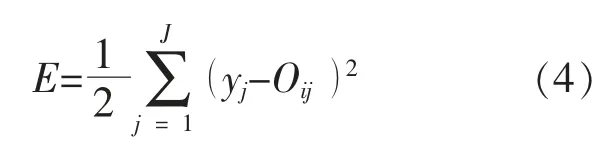
（2）误差的反向传递与权值阈值更新增量

从隐含层第l 个神经元到输出层第j 个神经元之间的连接权值的更新增量为

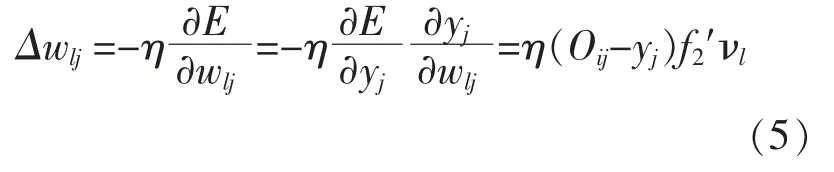
同理可得：

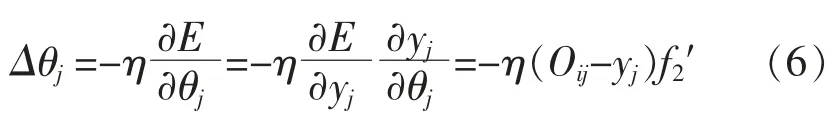
从输入层第m 个神经元到隐含层第l 个神经元之间的连接权值的更新增量为

同理可得：

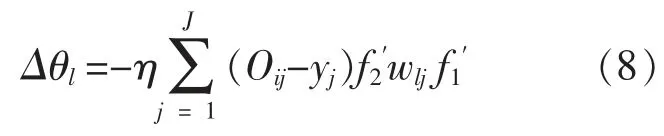
（3）网络权值阈值更新

根据上面求得的各层神经元连接权值及阈值变化增量来迭代更新下一轮网络学习与训练的神经元连接权值与阈值，更新公式为

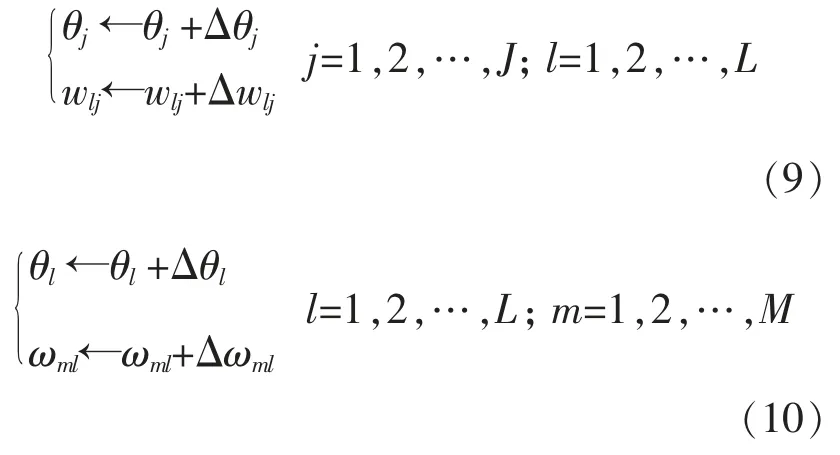
（4）训练完成

重复上述步骤直到网络全局误差小于预先设定的一个极小值，即网络收敛，训练完成。

1.2 LM-BP神经网络

由于上述普通BP 神经网络是根据梯度法的思想来对权值阈值进行修正的，当误差函数梯度为零时，可能会出现网络陷入局部极小值的问题，导致网络无法收敛。 为了解决这个问题，Levenberg-Marquardt 算法被提出，即通过将Hessian 矩阵分解为Jacobian 矩阵乘积后求逆以减少计算复杂度[13]。梯度法在最初几步下降较快，但随着接近最优值，由于梯度趋于零，致使目标函数下降缓慢；而牛顿法则可在最优值附近产生一个理想的搜索方向。Levenberg-Marquardt 法实际上是梯度法和牛顿法的结合，它的优点是网络权值数目较少时收敛非常迅速。

2 神经网络降维方法

2.1 PCA算法

主成分分析法（Principal Component Analysis，PCA）是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。它可以在数据信息损失最小的原则下，将高维变量空间进行降维处理，以消除变量多重相关性造成的信息相互重叠部分。

设数据集Xn×p，其中每一行对应一个样本（共n 个样本），每一列对应一个变量（共p 个变量）。对原始数据进行数据标准化处理：

式中：Sj为变量xj的样本标准差。

计算标准化数据矩阵Xn×p的协方差矩阵V。此时，V 又是 Xn×p的相关系数矩阵。

取满足下列条件的k 值：

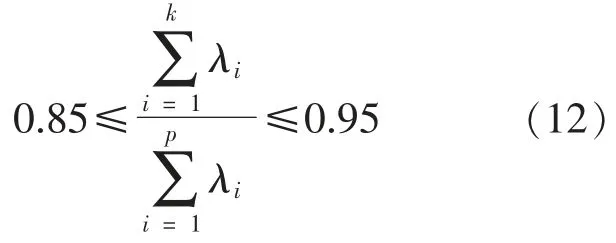
解方程Vξ=λiξ，得各个特征值对应的特征向量 ξi，得到第 i 个主成分：

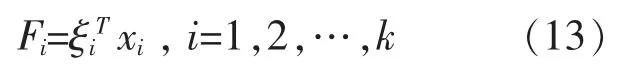
2.2 Garson算法

Garson 算法是用连接权值的乘积来计算输入变量对输出变量的影响程度，然后通过选择影响程度大的变量来对模型降维的方法。 与主成分分析法类似，Garson 算法也是选取k 个主要的影响因素，对模型进行降维。 其计算公式如下：

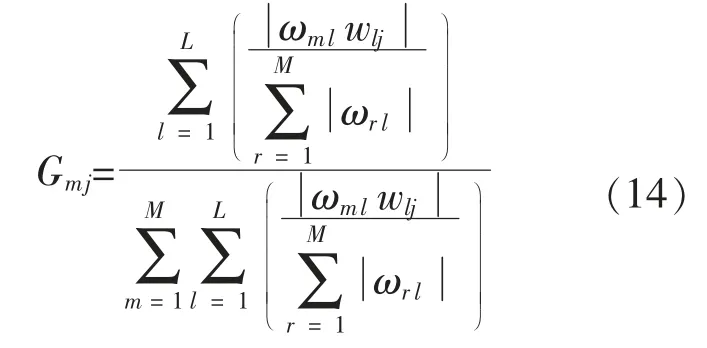
式中： l=1，2，…，L； m=1，2，…，M； j=1，2，…，J；Gmj为输入层的第m 个神经元对输出层的第j 个神经元的影响程度。

3 实例分析

3.1 LM-BP神经网络建模

3.1.1 原始数据

本文以某电厂的生物质锅炉为研究对象。研究过程中燃料不变，均为干料、木片和压块的质量比为 55∶5∶40 的混合料，仅考虑运行参数对飞灰含碳量的影响。 根据锅炉的燃烧系统[一次风温、二次风温、一次风量（高端）、一次风量（中端）、一次风量（低端）、总风量、燃烧室烟气温度、一级过热器出口烟气温度、 省煤器出口烟气温度、烟冷器出口烟气温度、排烟温度、烟气含氧量和汽水系统（负荷、给水温度、省煤器出口水温、四级过热器出口蒸汽温度、四级过热器出口蒸汽压力）选取了17 个变量作为模型的输入变量，飞灰含碳量作为输出变量。 取电厂2017 年8 月某25 天中每天3 组数据，一共75 组。 原始数据见表1。

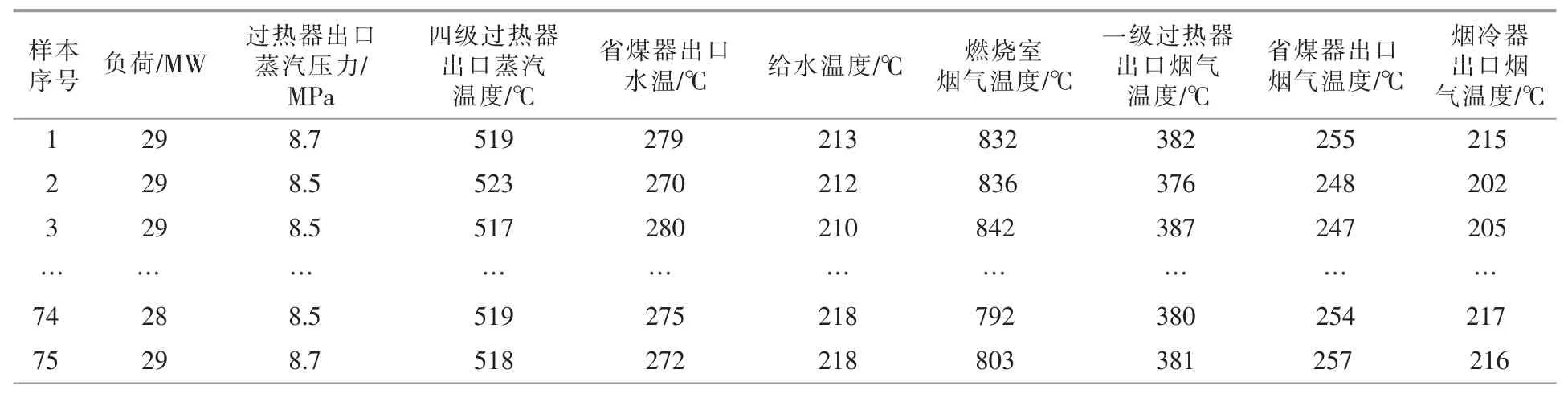
表1 原始数据Table 1 Raw datas for simulation

续表1

3.1.2 数据预处理

因各种数据的量纲不同，所以在数值上会存在很大的差异，从而不能真实反映数据本身的变化情况，影响模型准确建立。因此，须要对数据进行归一化处理。 本文所有工作均在MATLAB 2016b 软件平台完成。

设样本 xm的最大、最小值分别为 xmax，xmin，归一化处理后的数据为

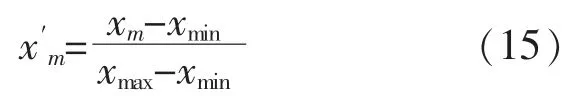
3.1.3 模型建立

将经过预处理后的数据分为两部分，一部分作为训练集用来进行网络的学习训练；另一部分作为测试集用来测试网络的泛化能力。

网络输入层神经元为17 个，输出层神经元为1 个，而隐含层神经元数通过经验公式得到，可能的隐含层神经元数由式（16）确定[14]，[15]。

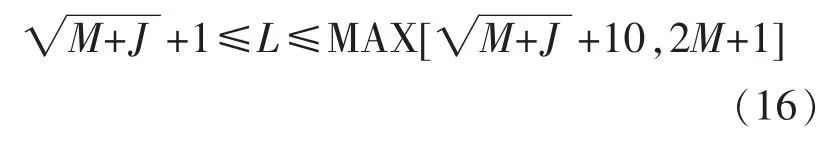
式中：M 为输入层的神经元数；J 为输出层的神经元数；MAX[a，b]为 a，b 中的较大者。

经过多次试验，最终确定隐含层神经元为11 个。 对表1，2 的数据进行归一化处理后，取表中1～67 对应的67 组样本数据用来训练神经网络，68～75 的 8 组数据用来验证网络。 设置最大训练次数为 100 次、学习率为 0.01、训练目标为0.000 01。

经过20 步网络收敛，为了验证模型的正确性，利用验证数据对已经训练好的模型进行了检验，结果如图2，3 所示。从图2，3 可以看出，模型预测值与实际值吻合程度一般，个别点的误差超过10%，模型须进一步降维改进。

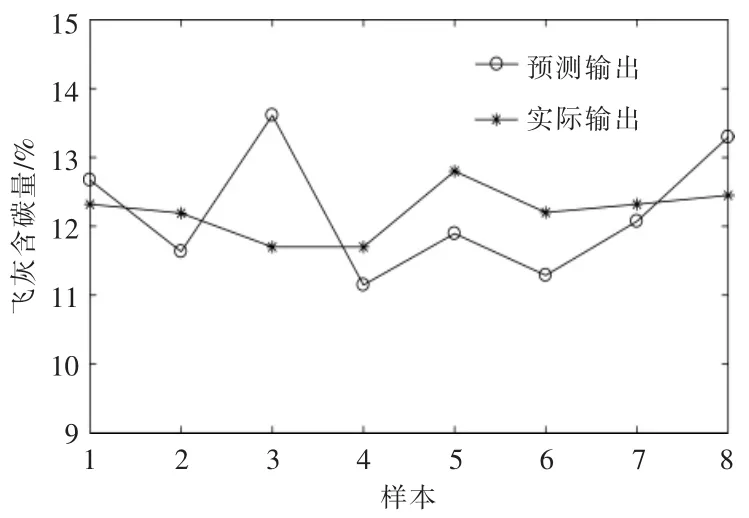
图2 LM-BP 神经网络预测值与实际值的比较Fig.2 Comparison of estimated and real values of LM-BP neural network model

图3 LM-BP 神经网络的相对误差Fig.3 Relative error of LM-BP neural network model

3.2 LM-PCA-BP神经网络建模

按照主成分分析法进行处理得到17 个特征根，按从大到小的顺序进行排列分别为3.761 3，3.464 0，2.296 1，1.705 9，1.199 4，1.011 5，0.821 1，0.671 6，0.523 6，0.468 4，0.321 1，0.242 6，0.189 7，0.159 9，0.103 9，0.047 6，0.012 3，取前8 个特征根，它们的贡献率分别为 22.13%，20.38%，13.51%，10.03%，7.06%，5.95%，4.83%，3.95%，累计贡献率为87.84%。 把这 8 个特征根所对应的特征向量与标准化后的数据矩阵相乘可得到前 8 个主成分值（表2），作为 LMPCA-BP 神经网络的输入参数。

表2 原始数据前8 个主成分值Table 2 First 8 principal components of Raw data

经过多次试验，最终确定隐含层神经元为12 个，网络设置同上。 经过39 步网络收敛，网络的验证结果如图4，5 所示。 从图4，5 中可以看出，模型预测值与实际值较为吻合，但仍有个别点误差较大。

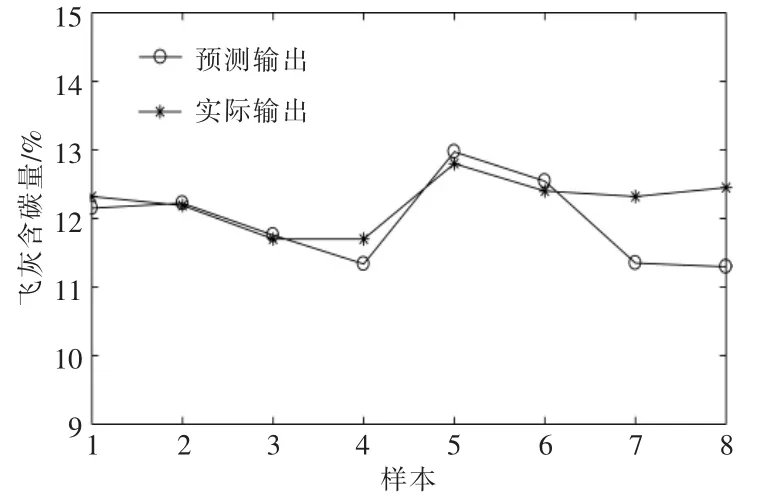
图4 LM-PCA-BP 神经网络预测值与实际值的比较Fig.4 Comparison of estimated and real values of LM-PCABP neural network model

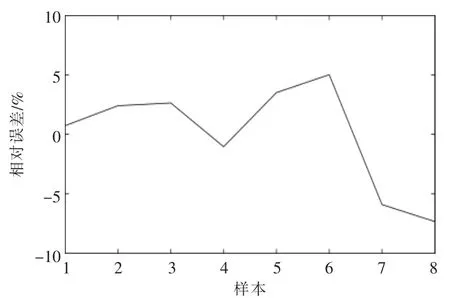
图5 LM-PCA-BP 神经网络的相对误差Fig.5 Relative error of LM-PCA-BP neural network model

3.3 LM-Garson-BP神经网络建模

取出LM-BP 神经网络收敛时的网络权值，引入Garson 算法对权值矩阵进行处理，得到17个输入变量对输出变量影响程度的相对大小如图6 所示。

图6 输入变量对输出变量影响程度的相对大小Fig.6 Relative influence of input variables on output variables

与PCA 的降维方法不同，Garson 算法降维时，选取参数没有固定标准，本文选取17 个输入参数中相对影响程度较大的8 个参数 （表3），作为LM-Garson-BP 神经网络的输入参数。 经过多次试验，最终确定隐含层的神经元为6 个，网络设置同上。 网络经66 步收敛，验证结果如图7，8 所示。从图7，8 中可以看出，模型预测值与实际值吻合程度进一步提高，误差较小且分布比较平均。

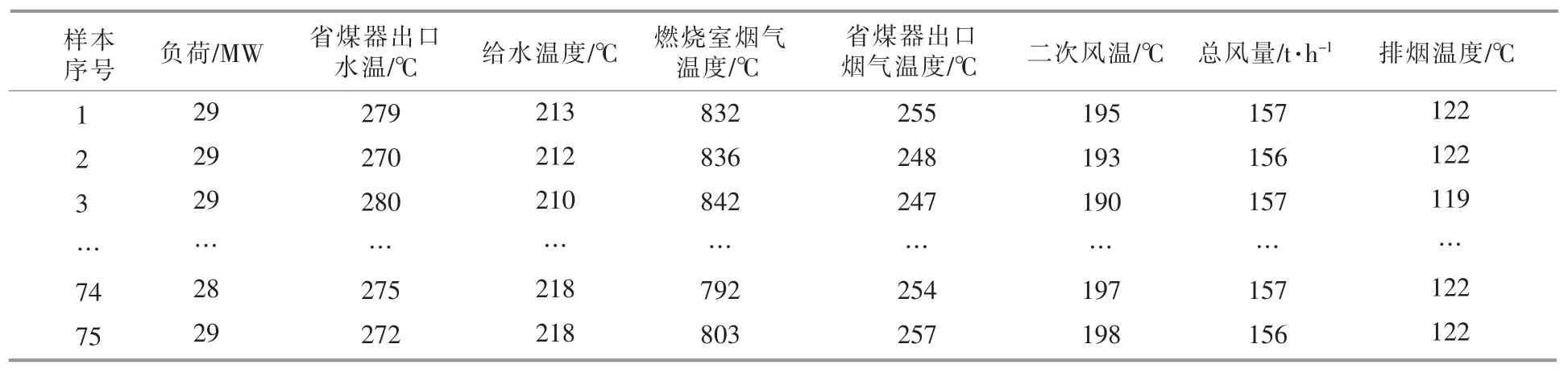
表3 8 个相对影响程度较大的输入变量Table 3 First 8 input variables with a high degree of relative influence

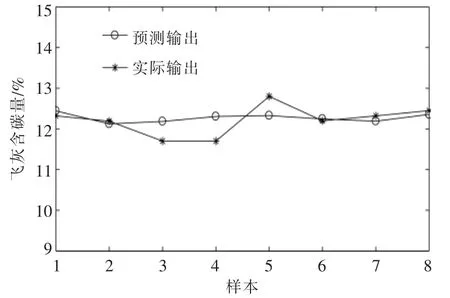
图7 LM-Garson-BP 神经网络预测值与实际值的比较Fig.7 Comparison of estimated and real values of LM-Garson-BP neural network model

3.4 3种网络的对比

为了更好地对3 种预测网络进行对比，引入误差分析指标均方误差：（Mean Square Error，MSE）、 平均绝对百分比误差 （Mean Absolute Percentage Error，MAPE） 和平均绝对误差（Mean Absolute Error，MAE）。其中，MSE 可以评估模型预测值的离散程度，MAPE 可以评估模型的预测泛化能力，MAE 能更好地反映预测值误差的实际情况[16]。

图8 LM-Garson-BP 神经网络的相对误差Fig.8 Relative error of LM-Garson-BP neural network model

式中：yi为输出层第i 个神经元的实际输出；Oi为输出层第i 个神经元的预测输出；N 为用于验证的数据组数。

总结3 种不同神经网络对生物质锅炉飞灰含碳量的预测结果，并计算它们的误差分析指标，结果见表4。

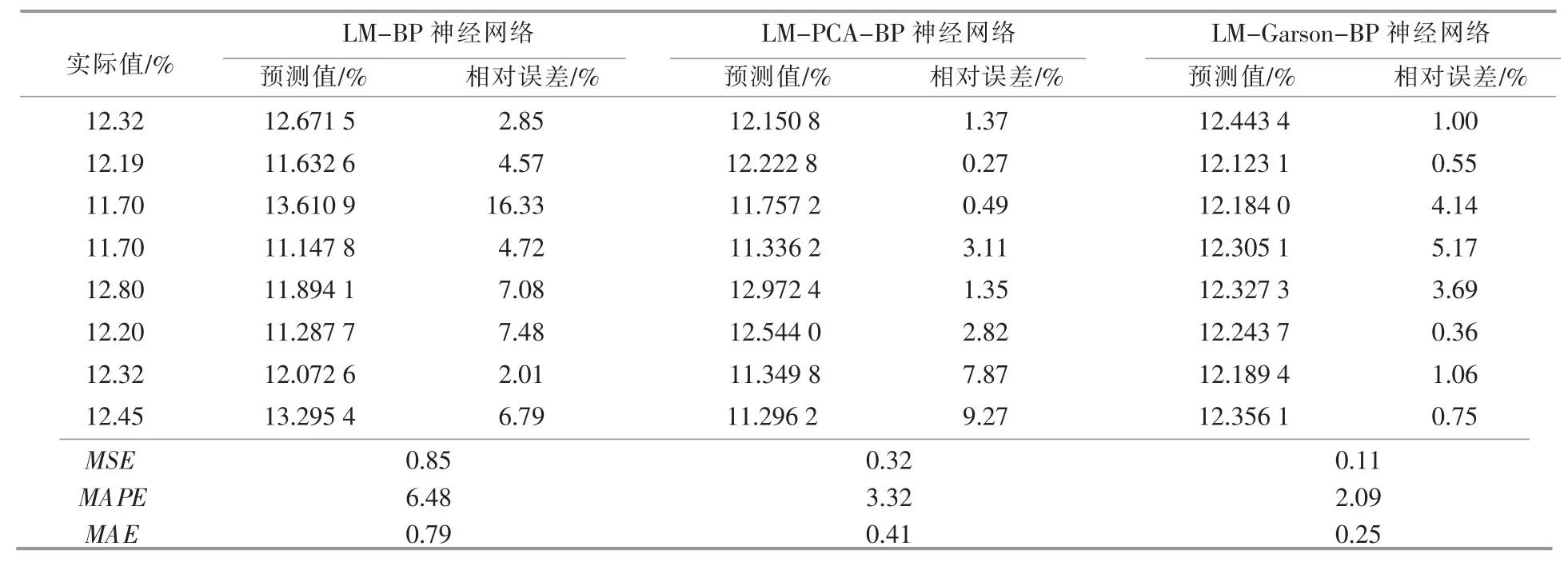
表4 3 种不同神经网络的预测结果对比Table 4 Comparison of three different neural networks

综合图2～8 和表4，我们可以准确分析各模型预测的结果优劣。

①LM-BP 神经网络的MAPE 为6.48%，最大相对误差为16.33%，最小相对误差为2.01%，模型的预测泛化能力最差；LM-PCA-BP 神经网络的MAPE 为3.32%，最大相对误差为9.27%，最小相对误差为0.27%，预测泛化能力较好；LMGarson-BP 神经网络的MAPE 为 2.09%，最大相对误差为5.17%，最小相对误差为0.36%，预测泛化能力最好。

②3 个 模 型 的 MSE 分 别 为 0.85，0.32 和0.11，离散程度越来越小，即LM-Garson-BP 神经网络的预测结果最稳定。

③LM-PCA-BP 神经网络和LM-Garson-BP神经网络均是通过降维方法对LM-BP 神经网络进行改良而得到的，但LM-Garson-BP 神经网络的改良效果更好。一方面，它的预测泛化能力和稳定性更好；另一方面，它在降维过程中可以对原始输入参数进行影响程度排序，对电厂进行参数优化具有指导意义，而LM-PCA-BP 神经网络得到的主成分没有实际意义。

4 结论

本文根据生物质锅炉的实际运行参数，建立了基于LM-BP 神经网络的生物质锅炉飞灰含碳量预测模型。 用PCA 和Garson 算法分别对LMBP 神经网络进行改良，通过比较不同的网络模型和预测结果可知，通过Garson 算法改良得到的LM-Garson-BP 神经网络的MAPE 为2.09%，MSE为 0.11，MAE 为 0.25，泛化能力最强，稳定性最好，而且可以对原始输入参数进行影响程度排序，能够为现场运行人员提供指导，具有一定程度的工程应用价值。