多场景下光伏-双单元储能系统协同平抑功率波动控制策略

颜晨煜，樊艳芳

（新疆大学 电气工程学院，新疆 乌鲁木齐 830047）

0 引言

近年来，光伏发电凭借其清洁无污染、可持续等优势得到了广泛应用[1]，[2]，但光伏出力具有一定的间歇性和随机性，若直接将其并网，将会给电力系统的稳定运行带来巨大挑战[3]。 如何有效平抑光伏出力的波动成为光伏电站大规模发展亟待解决的问题。

目前，学者们大多通过选取合理、有效的信号分析方法对原始出力进行分析，并利用储能技术协同改善光伏发电的电能品质，达到提高光伏并网可靠性的目的。 文献[4]利用低通滤波算法，并依据储能元件荷电状态 （State of Charge，SOC）对风电功率进行了分层优化，实现了功率波动的平抑以及储能元件的合理工作，但滤波时间常数难以准确控制，适用性较差。 文献[5]结合聚类经验模态分解法和模糊控制法，确定了各储能元件的功率分配，有效消除了聚类经验模态分解存在的模态混叠现象，但未充分考虑并网波动约束条件，且该分析算法存在频谱剖分效果不理想等问题。上述研究成果主要着眼于功率信号分析方法的选取，于是建立合理的储能系统、确定有效的控制策略就显得尤为重要。

由于储能系统能够实现电能的时空平移，且具有动态调节、快速响应等能力，因此被认为是抵消高渗透光伏发电负面影响的有效手段[6]～[8]。文献[9]将电动汽车作为储能元件，通过有序的充、放电达到平抑光伏功率波动的目的，但该方法忽略了电动汽车用户的个性化充电需求。 文献[10]利用氢储能系统平抑可再生能源的波动，并实现无污染物排放，但控制难度较大，工艺过程也较复杂。 文献[11]选用蓄电池与超级电容组成的混合储能系统，将不同的响应时间特性作为功率的划分依据，利用模糊控制原理保证储能元件工作在合理的区间内。 文献[12]对光伏出力的幅频特性进行分析，通过统计正负变换次数实现混合储能系统之间的功率分配。 文献[13]，[14]利用双级锂电池与超级电容组成多元储能系统，其中，超级电容能够吸收光伏功率波动中的高频分量，但是对于双电池系统所具有的可减小储能元件损耗、提高运行经济性的优点，该多元储能系统未能充分利用。

综上可知，虽然学者们对储能系统内部的功率的划分符合储能系统的性能特点，但未充分考虑储能系统的实际运行情况，导致分析结果的精度较低，且模糊控制过程中相关参数的选择大都基于经验，缺乏理论依据，一些错误的经验会降低系统计算结果的精度。

本文在前人研究成果的基础上，利用不同典型场景下光伏出力的波动特性，结合并网限制的要求，对光伏出力信号进行变分模态分解，确定并网目标功率和储能需求功率，并利用阈值补偿方法缩短计算时间。 为了减少储能消纳的能量波动频率，提高储能元件的运行寿命，在标准充、放电深度限制下，提出充、放电过程互补的双单元储能系统协同控制策略，能够有效平抑光伏出力波动，同时减小储能元件的损耗，提高储能系统运行的经济性。 研究结果对光伏电站大规模并网的发展具有一定的现实意义。

1 变分模态分解在平抑光伏出力波动中的应用

1.1 变分模态分解

变分模态分解（Variational Mode Decomposition，VMD）是一种新型信号分析算法。 其本质是对约束变分问题进行建模与求解，通过预设分解尺度K，将原本复杂的输入信号f（t）分解成K 个有限带宽的本征模态函数xk（t），且这些子模态函数xk（t）中绝大部分紧紧围绕在其所对应的中心频率 ωk（t）周围。

由于VMD 具有坚实的理论基础，鲁棒性良好，并且在相似子模态信号的分离与重构方面具有优良的性能，因此本文着重介绍变分问题的构造与求解。 VMD 的计算流程等详见文献[15]。

含约束条件变分问题的模型表达式为

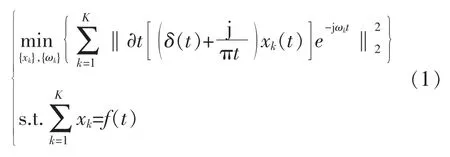
式中：f（t）为输入信号；t 为时间；xk（t）为谐波信号，该谐波信号的幅值为 Ak（t）、瞬时频率为 ωk（t）；{xk}为所有子模态的集合，{xk}={x1，x2，…，xK}；k为1 到K 之间的正整数；ωk为各子模态相应的中心频率，{ωk}={ω1，ω2，…，ωK}；δ（t）为脉冲函数。

为了解决上述变分问题，本文引入惩罚因子α 和拉格朗日乘子λ，将含约束条件的变分问题转化为非约束变分问题，并采用惩罚算子交替方向法，交替更新寻求最优解（n 为迭代次数），最后利用傅里叶变换将子模态函数更新至频域，求得更新后的子模态及其对应的中心频率。

更新后的子模态及其对应的中心频率的计算式分别为

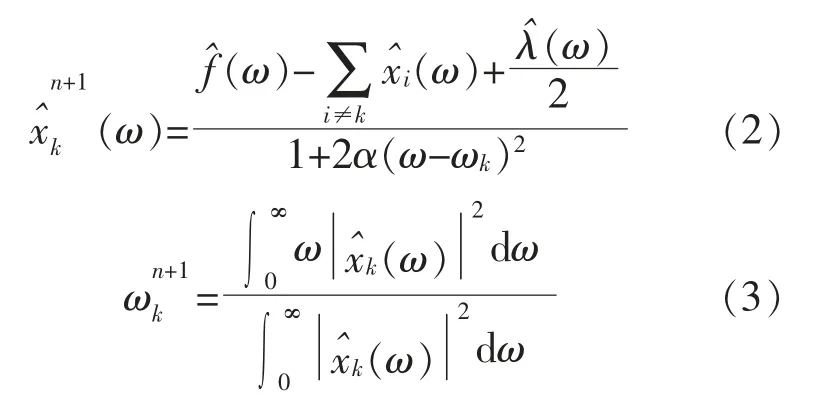
1.2 基于阈值补偿的变分模态分解算法

为了避免光伏出力波动对电网稳定运行的影响，国家电网公司对光伏电站接入电网有功功率变化的最大限制提出了相关要求[16]，以装机容量为15 MW 的小型光伏电站为例，规定其10，1 min内最大有功功率变化值分别不应超过其对应装机容量、0.2 MW。 在对光伏原始出力进行分析时，若对其出力平稳情况未进行预前判断，即使该时段出力情况满足光伏并网限制要求，也会由于不必要的分解而延长计算时间。

本文的试验是在两个场景下进行的。其中，场景1 为非晴天，场景2 为晴天。 不同场景下，光伏原始功率以及无阈值补偿的并网目标功率随时间的变化情况如图1 所示。 由图1 可知，典型场景1，2 下，不加以判断时所得的并网目标曲线与光伏原始出力曲线之间均有一定程度的延迟。

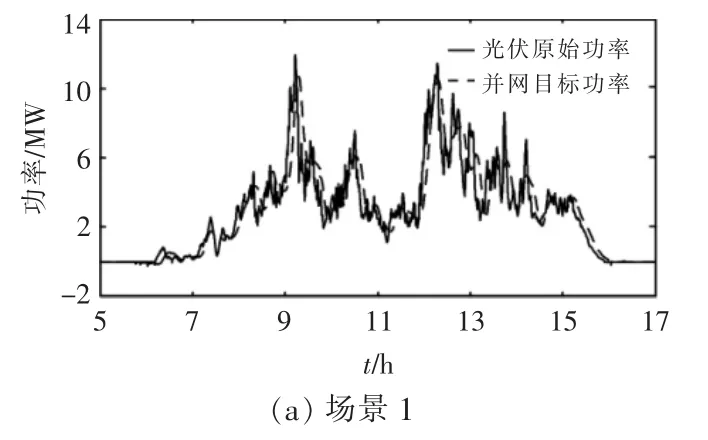
图1 不同典型场景下，无阈值补偿的并网目标功率以及光伏原始功率随时间的变化情况Fig.1 No-threshold compensation of the grid-connected target power and original photovoltaic power in difficult typical scenes

根据以上分析结果，本文提出了阈值补偿控制原理，在充分发挥VMD 优良模态分离性能的基础上，对数据进行预先判断，达到缩短计算时间的目的。

10，1 min 的阈值计算式分别为

式中：S1（t），S2（t）分别为 10，1 min 的阈值；PW，10（t），PW，1（t）分别为 10，1 min 时段内的光伏原始功率。

根据并网限制要求和实际光伏电站的类型，本文所选取的阈值波动允许范围为

具体的阈值补偿流程：①对时间t、光伏原始出力PW（t）进行初始化，设定阈值波动的允许范围；②读取光伏原始功率数据，选取10 min 时段内光伏原始功率的最大值 maxPW，10（t） 和最小值minPW，10（t），并根据式（4）计算出阈值 S1（t），判断S1（t）是否满足阈值波动允许范围，若满足，则进行下一步骤，若不满足，则直接对光伏原始功率进行 VMD 分解，使其子模态 1 分量 Pk=1（t）满足并网限制要求；③将步骤②中满足10 min 时段阈值范围的 PW（t）在 1 min 时段内进行判断，根据式（5）计算阈值 S2（t），并判断 S2（t）是否满足阈值范围，若满足，说明此时段光伏原始出力满足并网限制要求，不须分解就可以直接并网，若不满足，则对光伏原始功率进行VMD 分解，使其子模态1 分量Pk=1（t）满足限制要求，并循环步骤②，③，直至计算时间结束或满足阈值范围。

2 光储协同平抑功率波动系统结构

为使光伏发电系统具有清洁环保的特性，因此选择绿色新型磷酸铁锂电池构建A，B 储能单元，每个储能单元均由多个电池元件串、 并联构成。利用A，B 储能单元共同组成配置在光伏电站侧的双单元储能系统。 该协调互补的双单元储能系统对光伏电站的原始出力波动进行有效平抑，使平抑后的目标功率满足并网功率波动标准。

本文所提出的协同控制策略根据A，B 储能单元的运行状况确定双单元储能系统的充、 放电任务，通过变流器控制系统对A，B 储能单元中变流器的动作情况进行控制。 当变流器在整流状态下工作时，双单元储能系统储存能量；当变流器在逆变状态下工作时，双单元储能系统释放能量。与双单元储能系统相对应的光储协同发电系统拓扑结构如图2 所示。 图中：PW（t）为 t 时刻光伏电站的原始出力；PA（t），PB（t）分别为 t 时刻双单元储能系统中 A，B 储能单元的充、放电功率；Pout（t）为t 时刻并网目标功率。

图2 光储协同发电系统拓扑结构Fig.2 Structure of combined photovoltic-energy generation system

为了避免光伏功率波动平抑不足或过量，先利用阈值进行判断，而后根据国家标准，对波动剧烈的光伏原始出力信号PW（t）进行变分模态分解，使其分解后得到的子模态1 分量Pk=1（t）满足各时间尺度下的波动限值要求，将该分量作为并网目标功率Pout（t），并进一步确定双单元储能系统的需求功率PD（t）。 上述相关功率的关系式分别为

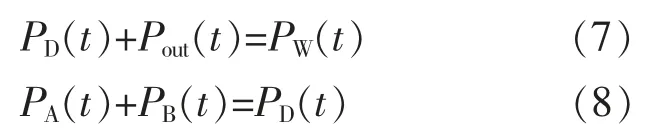
3 基于双单元储能系统的协同控制策略

3.1 双单元储能系统数学模型的建立

储能系统可以有效地平抑光伏出力的波动，抵消可再生能源高渗透率所引起的负面影响。 本文摒弃由蓄电池与超级电容器组成的传统混合储能系统，避免引用不精准的响应时间划分方法，提出利用磷酸铁锂电池构成双单元储能系统，以达到平滑效果。 将储能系统分为A，B 两个储能单元，当A 单元处于充、放电状态时，B 单元则处于待机状态，反之亦然。因此A，B 单元的额定充、放电能力均为整个储能系统的1/2。

各储能单元和储能系统额定功率和额定容量的关系式分别为

A，B 储能单元的SOC 递推公式为

式中：SA（t），SB（t）分别为 t 时刻，A，B 储能单元的SOC；ZAc，ZAd分别为 A 储能单元的充、放电运行的标志位；ZBc，ZBd分别为 B 储能单元的充、 放电运行标志位；ωc，ωd分别为 t 时刻，双储能单元是否执行充、 放电任务的标志位；ηc，ηd分别为储能单元的充、放电转换效率。

储能单元的充、放电状态及其充、放电标志位见表1 所示。 表中：Ae，Be分别表示 A，B 储能单元处于停止工作状态；Ac，Bc分别表示 A，B 储能单元处于充电工作状态；Ad，Bd分别表示 A，B 储能单元处于放电工作状态。

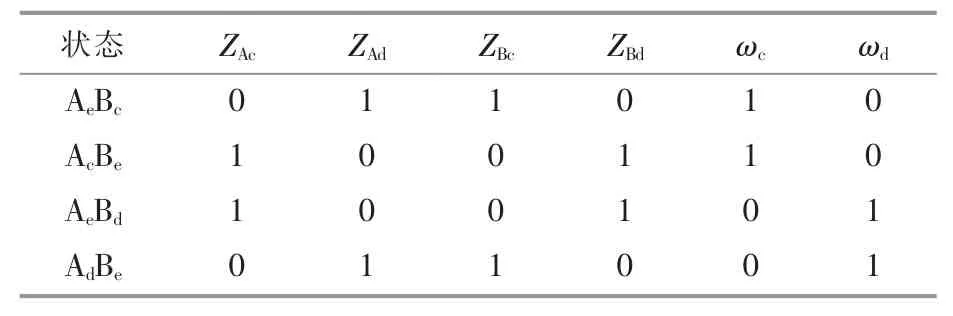
表1 储能单元的充、放电状态及其标志位关系对照表Table 1 Comparison table of charge and discharge states of energy storage units and their state marks

由 A，B 储能单元的 SOC 递推公式[式（10）]和状态标志位表[表（1）]可以看出，基于双单元储能系统的协同控制过程是一个多阶段决策过程。双单元储能系统完成一次充、 放电循环过程须经历多个阶段，不同阶段对应不同的SOC 递推公式，同时也对应着不同的控制机制。在本文所提出的协同控制策略下，双单元储能系统能够在标准充、放电深度内保持运行，显著减少了充、放电循环的次数，从而提高了储能元件的使用寿命和经济效益。

3.2 基于双单元储能系统的协同控制策略

为了解决储能系统充、 放电任务切换频繁的问题。 本文基于双向互补的双单元储能系统建立协同控制策略，使A，B 储能单元能够共同承担储能需求功率 PD（t）。 在运行状态下，若 A 或 B 储能单元的SOC 首先达到充电临界状态或放电临界状态，无论另一个储能单元处于何种工作状态，均会通过协同控制系统向变流器控制系统下达命令，以控制变流器的动作，切换两储能单元的充、放电工作状态。 图3 为双单元储能系统的协同控制流程图。 图中：T 为协同控制过程的最终时刻；Dref为储能单元的标准充、放电深度，可由厂家所提供的生产数据并结合文献[14]所提出的计算方法得出。

图3 双单元储能系统的协同控制流程图Fig.3 Dual units energy storage system collaborative optimization control process

由图3 可知，在此协同控制过程中，首先假定初始运行状态为A 储能单元承担放电任务，B 储能单元承担充电任务，由于当储能元件充、放电深度为标准深度时，对储能元件寿命的衰减程度影响较小，故设A，B 储能单元均工作在标准充、放电深度下，其中，A 储能单元的初始 SOC 为 （1+Dref）/2，B 储能单元的初始 SOC 为（1-Dref）/2。 若 SA（t）达到放电临界值（1-Dref）/2，或 SB（t）达到充电临界值（1+Dref）/2，则立即交换锂电池的 A，B 储能单元运行模式，即A 储能单元由初始放电状态转换成充电状态、B 储能单元由初始充电状态转换成放电状态。同理，在下一阶段，若SA（t）达到充电临界值（1+Dref）/2，或 SB（t）达到放电临界值（1-Dref）/2，则继续交换 A，B 储能单元的运行模式，如此循环，直到协同控制过程的最终时刻。 即当A，B 储能单元中任一单元达到临界状态时，储能系统立即切换充、放电模式，且A，B 储能单元不同时处于充、放电工作状态。

4 仿真验证

为了验证多场景下本文所提出的功率信号分析算法以及基于双储能单元的协同控制策略的优越性，本文在MATLABsimulink 平台上进行模拟仿真，以国内某总装机容量为15 MW 的光伏电站为研究对象，以典型工况下的光伏出力 PW1（t），PW2（t）为研究目标，采样间隔为 1 s。

近年来，许多地区已经对古树名木进行了摸底调查，但调查指标设置不合理，数据较为粗放，不能准确反映当前古树名木的生存现状。笔者以济源市王屋镇为例，通过设置一些完善的调查指标，对古树名木的树种构成、生长状况、存在问题等进行调查分析，并针对性地提出一系列保护措施，以期为古树名木调查指标的合理化、标准化提供参考，也为古树名木的精准保护提供支持。

由于光伏出力具有明显的时间分段性，因此本文重点研究5：00-17：00 的光伏出力。储能系统采用磷酸铁锂电池，该储能系统由2 个额定容量均为 4.5 MW·h 的储能单元 （A，B 储能单元）组成，A，B 储能单元的充、 放电转换效率均为0.9，初始运行状态为A 储能单元承担放电任务、B 储能单元承担充电任务，标准充、 放电深度设定为0.95。通过计算可得到，A，B 储能单元的初始SOC分别为 0.975，0.025。

4.1 多场景下基于阈值补偿的光伏出力VMD平滑效果分析

为了验证多场景下，本文所提出的基于阈值补偿的VMD 分解算法的普适性，依据光伏并网波动的限制要求，将波动较剧烈的典型场景1 的分解尺度设定为6、 波动较平缓的典型场景2 的分解尺度设定为5，并将所得出的子模态1 分量Pk=1（t）作为并网目标功率与光伏原始功率进行比对，如图4 所示。

图4 不同典型场景下，并网目标功率随时间的变化情况Fig.4 Changes of grid-connected target power over time in different typical scenes

由图4 可明显看出，相对于光伏原始输出功率曲线，经过VMD 处理得到的并网目标功率的波动频率较低，且该波动频率能够表征光伏功率信号的整体态势。 此外，通过阈值补偿后，缩短了由于不必要的计算分析所造成的延迟时间。 在满足并网限制要求的前提下，根据实际储能容量等级，可将阈值范围进行合理调整。

为了验证不同典型场景下所选分解尺度的准确性，对比分析了不同的取值间隔以及场景条件下，并网最大有功功率变化量随时间的变化情况，如图5 所示。 由图5 可明显看出，场景 1，2 下，1，10 min 级的最大有功功率变化量均没有超出并网波动限制要求的情况出现。 表明不同典型场景下，基于阈值补偿VMD 算法平抑光伏功率波动的适用性较好。

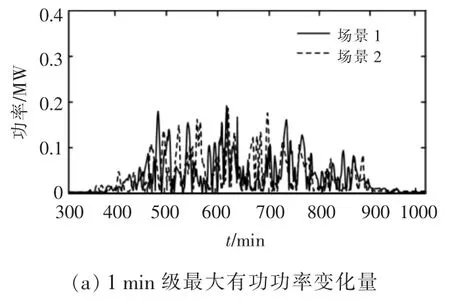
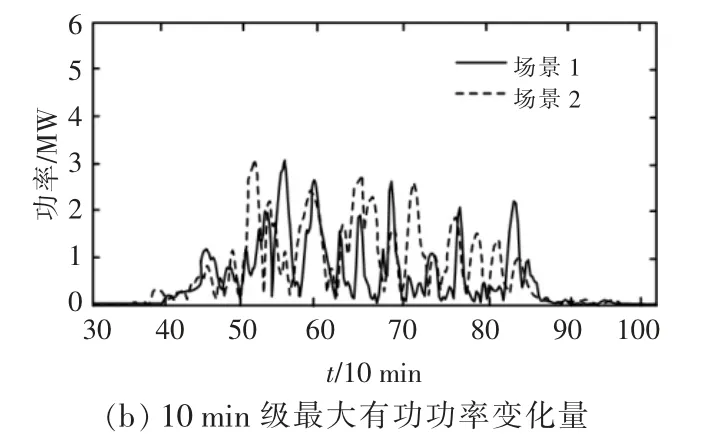
图5 不同的取值间隔以及场景下，并网最大有功功率变化量随时间的变化情况Fig.5 Changes in the maximum of grid-connected power variation over time in different value intervals and scenes

4.2 多场景下双单元储能系统协同控制策略验证

上文基于光伏并网波动限制要求，对典型光伏出力场景进行分解，得到场景1 下的分解尺度为6、场景2 下的分解尺度为5。 多场景下光伏原始功率经VMD 分解后，子模态1 分量成为并网目标功率Pout（t），将剩余子模态分量进行重构，作为储能需求功率。

除了并网目标功率外，场景1 中子模态2～6分量[Pk=2（t）～Pk=6（t）]随时间的变化情况如图6（a）所示。 场景 2 中子模态 2～5 分量[Pk=2（t）～Pk=5（t）]随时间的变化情况如图6（b）所示。

目前，储能系统内部能量的划分方法大多利用能量型储能与功率型储能之间不同的响应特性实现功率分配。 一般选用1 min 作为划分界限，但该划分方法没有充分考虑实际情况下各储能元件的运行状态，因此不够严谨，且没有考虑功率型储能元件初期建设成本较高的问题。 故本文将储能系统划分为双向互补的A，B 储能单元，这两个储能单元共同对储能需求功率进行消纳。

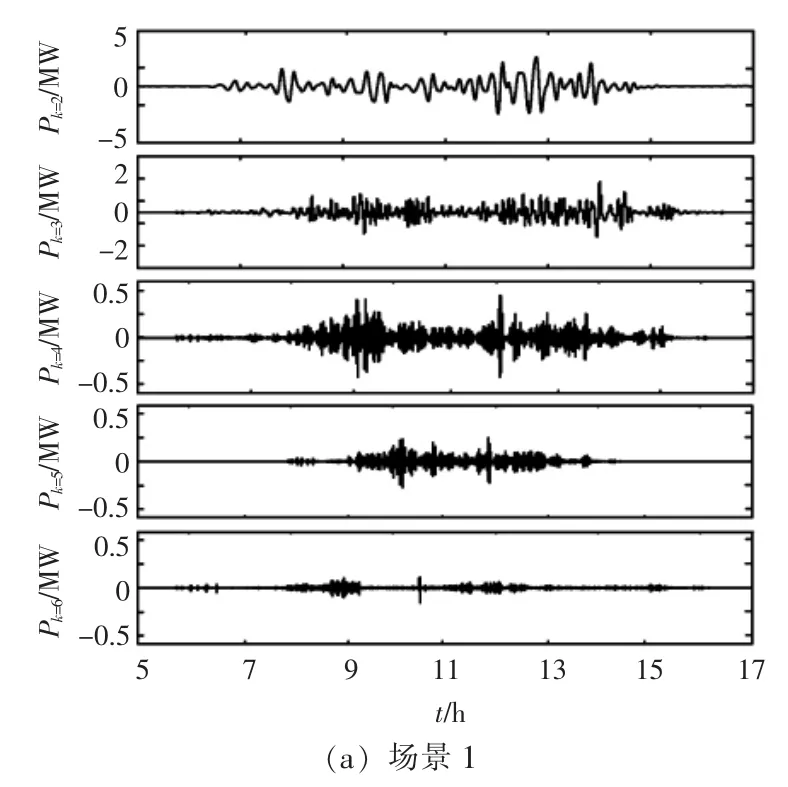
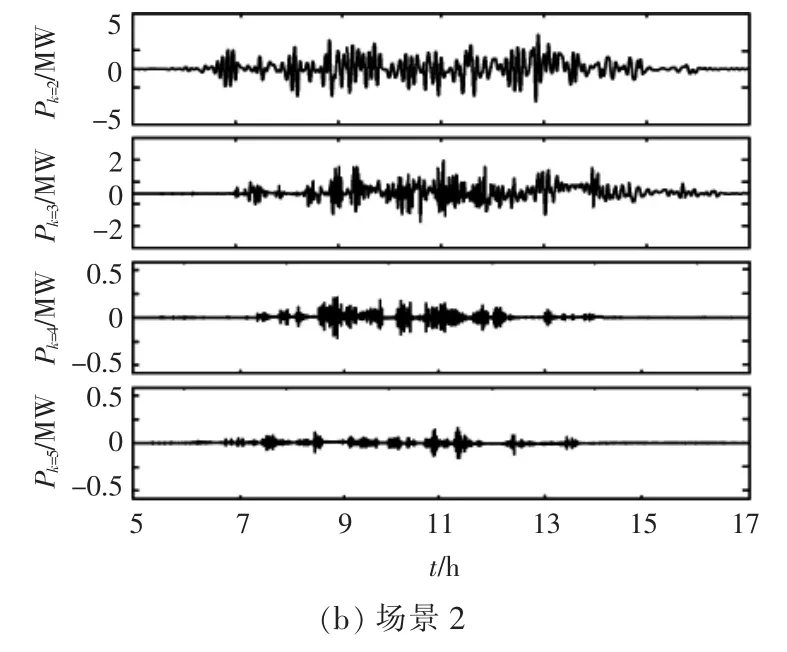
图6 不同典型场景下，子模态功率分量随时间的变化情况Fig.6 Changes of sub-modal power component over time in different typical scenes

图7 不同典型场景下，优化后的各储能单元SOC 随时间的变化情况Fig.7 Changes of optimized SOC of each energy storage unit over time in different typical scenes

由图7 可知，基于双储能单元协同控制优化后，场景 1 下 A，B 储能单元分别在 9.6，11.3，12.8，14.2 h 切换运行状态，场景2 下A，B 储能单元分别在 9.2，11.5，13.2，14.6 h 切换运行状态。 这样有效地避免了粗糙的储能响应时间的划分，同时保持A，B 储能单元持续在最佳充、放电循环深度范围内工作，显著降低了各储能元件的充、放电频率以及寿命衰减程度、 有效提高了储能系统运行的经济性。

图8 为采用双储能单元协同控制优化后，各储能单元储能需求功率随时间的变化情况。

图8 不同典型场景下，优化后的各储能单元需求功率随时间的变化情况Fig.8 Changes of optimized demand power of each energy storage unit over time in different typical scenes

A，B 储能单元需求功率的总和为优化控制前的储能需求功率。由图8 可以看出，优化前的储能需求功率（A 储能单元需求功率）不仅波动幅度较大，波动频率也较为频繁，若此时的储能需求功率直接由单储能系统进行承担，将会对储能元件造成严重损耗，且会降低储能元件的正常运行寿命。经双储能单元协同控制策略优化后，显著降低了各储能单元的充、放电幅度及频率，且各储能单元的运行状态转换时刻与储能单元SOC 到达临界值的时刻相对应，证明了所提出的协同控制策略的有效性及合理性，提高了储能系统的使用寿命和经济效益。

5 结论

本文针对多个场景下的光伏出力波动特性，结合光伏并网的限制要求，对光伏原始功率信号进行变分模态分解，同时提出了在协同控制策略下可独立承担充、放电任务的双单元储能系统。根据仿真结果得到如下结论。

①在不同的场景下，光伏原始功率经VMD算法分析后，所得并网目标功率均满足并网限制要求，且功率波动得到了有效的平抑，同时通过阈值补偿方法，缩短了不必要的计算延时。

②经双储能单元协同控制优化后，各个储能单元均能持续地运行在标准的充、 放电循环深度范围内，显著地减少了单储能系统充、放电频繁等问题，延长了储能系统的使用寿命和运行经济性。

后续的工作将针对光伏电站的在线实时控制以及储能元件容量的经济性优化等方面展开进一步的研究。