土颗粒形态的二维数学表达及其适用性

李 强,乔志甜,沈 伟,李 萍,李同录

(长安大学地质工程与测绘学院,陕西 西安 710054)

黄土颗粒的形态是极为重要的,它很大程度上影响黄土天然结构与湿陷性[1]。所以在微观土体建模方面,黄土颗粒形态应尽量符合实际。土颗粒形态的描绘方法最初起源于图形学。在图形学上,形态是图形的多个基本特征之一[2],也是进行图形分析和图形识别的重要途径。目前,已有的土颗粒形态描绘方法可分为2类:一类是基于区域形态函数法,这种方法常用力矩阵理论来描绘颗粒形态[3-4],其中力矩类型包括几何矩、Legendre矩和Zernike矩等。区域形态描绘法将闭合曲线所包围的区域看作一个整体,对区域内所有像素点进行整合,故能反映曲线内部的情况。另一类方法基于边界形态描绘法,包括Hough变换法[5-6]、Fourier法[7]以及小波变换法[8-9]。该方法通过提取轮廓信息来描绘形态,所以仅能描绘形态的边界形态,而其区域内部的形态得不到反映。

对于二维土颗粒,在建立其微观力学模型时仅需要给出颗粒的外边界形态,因此边界形态函数法就能满足要求,其中Fourier法是目前应用最广、可扩展性最高的一种边界形态描绘方法。该方法已在建筑、地质、古生物等领域得到广泛应用。例如,Wang 等[10]利用Fourier法定量分析了水泥中粗骨料形态的几何特征;Ehrlich等[11]发现Fourier法可以量化颗粒形态,这些量化指标包含大量的地质信息;Bowman等[12]通过定义Fourier描绘符来定量分析砂粒在不同地理位置以及在受到不同冲刷作用下的形态差异;Khouya等[13]采用Fourier法描绘化石的形态并对化石分类。虽然Fourier法具有计算简单,灵活性高等优点,但也存在一些不足,如在需要较高的拟合精度时,该方法需要采集大量的样本点,构建过程繁琐;有限的Fourier级数虽能较好地描绘颗粒形态,但无法使拟合曲线通过采样点,因此以此构建的力学模型将不能精确判断颗粒的接触位置和范围。针对Fourier法的不足,分别用Lagrange函数、Hermite函数以及Spline函数构建3种新的颗粒形态描绘方法,而后利用它们对甘肃正宁的实际黄土颗粒的形态进行描绘,根据结果探讨了这4种方法各自的特点及适用性。

1 二维土颗粒形态的描绘方法

1.1 Fourier函数法

Fourier函数[12]可表示为

(1)

其中:ai、bi为Fourier系数;i为频率;R为距离参考形心的半径;θ为采样点方位角。

在使用Fourier函数时,形态的参考形心位置需精确定位:

(2)

选取样本点后,Fourier系数ai、bi可由最小二乘法确定。Garboczi等[14]发现Fourier系数ai、bi随i增加而降低,并逐渐趋近于0。根据Wang等[15]的研究,式(1)中i≤4的部分为形态描绘项,主要控制图形的拉伸;i≤25的部分为角度描绘项,主要控制颗粒表面较大的起伏;此外,i≥26的部分为表面纹理描绘项,主要控制颗粒表面较细微的结构。因此使用有限的Fourier项数就能较好地描绘颗粒形态。

1.2 Lagrange函数法

通过Lagrange插值函数可以对二维平面上若干个已知点的分布函数进行插值,其原理是通过已知的n+1个节点值拟合出一个n次多项式。函数形式为

(3)

其中:Ri为样本点半径;li为Lagrange基函数,li表达式为

(4)

当函数次数<7时,Lagrange函数的插值结果较好[16],随着次数的增加,误差将会增加,这种现象被称为Runge现象。

1.3 Hermite函数法

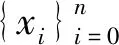
(5)

其中:ii(θi)可由式(4)求导获得。

1.4 Spline函数法

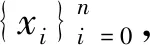
以往的民间文学(民间故事)经典研究，都是立足于民间文学学科本位，通过对民间文学对象的题材内容、结构形态等认识达到外在的、主观的、实然的实践目的，即对“真”的追求。此种研究从独立于、优越于实践的认识主体立场出发，无论怎样归纳诸种价值范畴，其思考结果都必然是外在的，都依赖于民间文学对象的外在语境。一旦外在语境消失，就丧失了实然(真)的发生条件与存在理由，在认识主体(研究者)眼中，民间文学即面临着消亡命运。

(6)

其中:Mi为系数;hi为区间长度,其形式为

hi=(xi-xi-1)。

(7)

三次样条插值函数在每一个小区间上是不超过3次的多项式,含有4个待定系数,在整个区间上有4n个待定系数,依据三次样条插值函数的定义,可确定4n-2个约束条件。要确定4n个系数需附加2个约束条件。为了保证轮廓曲线在连接点处光滑,选择转角边界条件。

1.5 示例

由于Lagrange和Hermite函数存在Runge现象,在描绘颗粒形态时,应分段对颗粒进行描绘。此外,在应用上述4种函数法时,须保证角度(θ)与半径(R)一一对应。研究举1例说明了各个函数的特点。

图1为文献[14]中一个任意形态土颗粒,定义其边界到中心的半径为R,角度为θ,利用上述4种函数对其形态进行描绘,说明采样点选取即参数计算方法。每隔1度选一个采样点,共360个点来控制土颗粒的真实形态。不同采样点数下各方法对给定土颗粒的描绘效果见图2。图2中4种函数法所使用的采样点都为等间距均匀采样。

由图2可知,从拟合结果的形态上来看,随着采样点数的增加,4种函数法的拟合结果都逐渐趋近于实际形态。

图1 不规则形态土颗粒示意图Fig.1 Schematic diagram of soil particles with irregular morphology

对于Fourier法,当采样点数N≤60时,拟合结果的形态与原始颗粒有较大差距;当采样点数N≥60时,拟合结果的形态与原始形态较为接近,且随着采样点数的进一步增加,拟合结果在形态变化上趋于稳定,但最终仍无法与原始形态完全重合。

由于Lagrange和Hermite函数均存在Runge现象,因此在使用Lagrange和Hermite函数法时,需对实际颗粒分段描述,分段的段数必须满足在各分段内不会出现Runge现象。

对于Lagrange函数法,当采样点个数为20和36时,在形态上,各分段的连接点附近与原始形态有较大误差,这是由于Lagrange函数在连接点处的导数不连续。经试算发现,当在各分段连接点处密集采样时,能够保证在点数较少的情况下,降低连接点附近在形态上的误差(见图3)。此外,当采样点数N≥60时,各分段连接点处误差相对较小。

对于Hermite函数法,因该函数为带导数型插值函数,故在各分段连接点附近没有出现由于不可导而造成的误差现象。

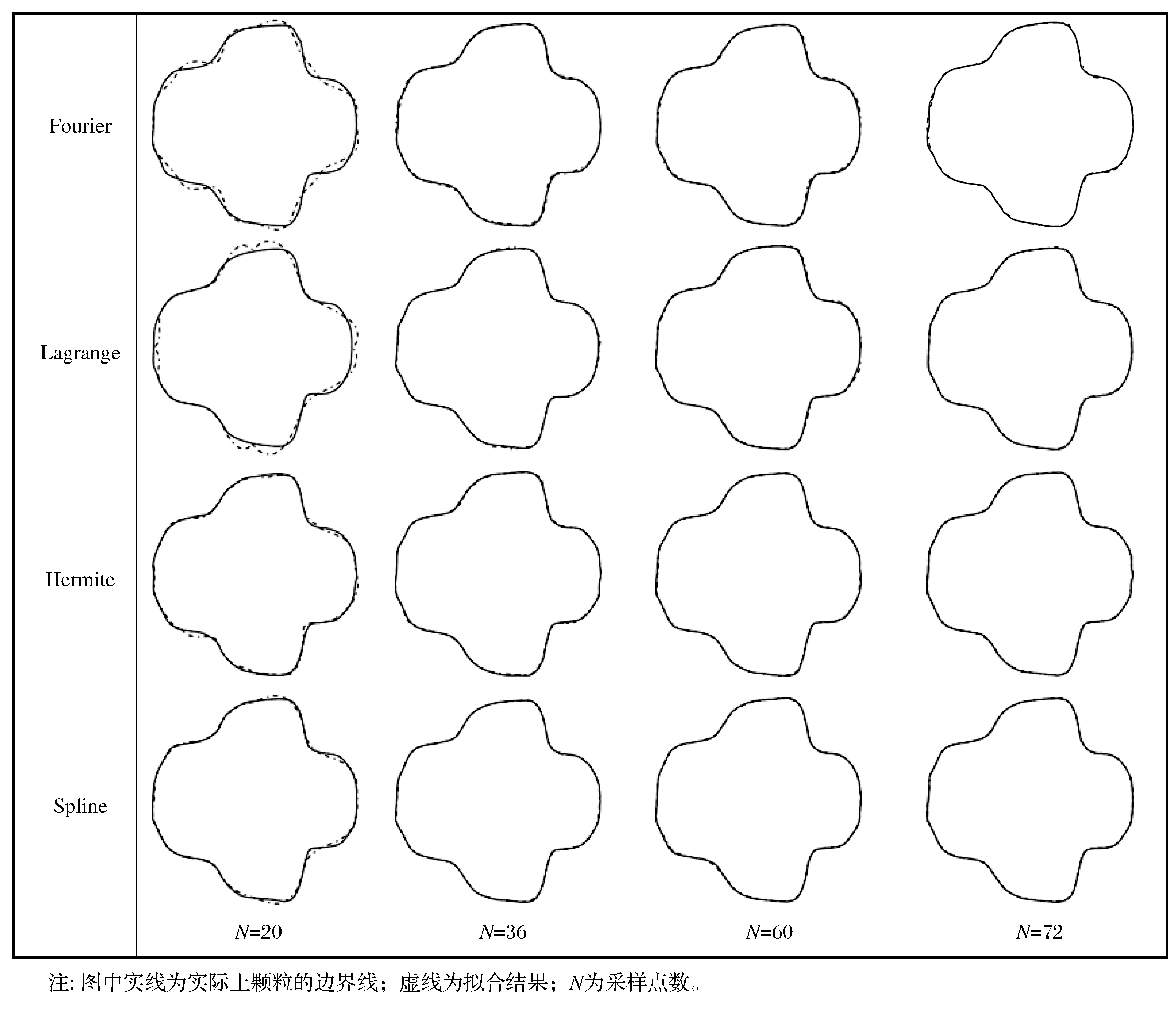
图2 不同采样点数下各方法对给定土颗粒的描绘效果Fig.2 Schematic diagram of the effect of depicting a given soil particle with different sampling points by using different methods

图3 Lagrange函数法描绘结果 Fig.3 Lagrange function method depicting effect

对于Spline函数法,当N=20时,拟合结果的形态与原始图形的形态有较大的差距,其原因在于采样点较少且间隔较大。当N进一步增加,采样点间隔变小时,拟合结果的形态逐步趋近于原始颗粒形态。

当采样点数N≤36时,Hermite和Spline函数法的描绘结果相对于其他2种函数法更接近于原始形态,这是由于Hermite函数为带导数插值函数,其插值精度相对高于其他方法。Spline函数是一种分段插值函数,对复杂曲线的刻画能力较强。当采样点数N≥60时,相对于其他3种函数法,Fourier法的拟合结果最差,其他3种函数法的拟合结果都与原始形态极为接近。这种现象是由于研究使用有限Fourier级数来代替无穷项Fourier级数。此外,随着采样点数的进一步增加,4种函数法的拟合结果在形态上的变化基本趋于稳定。

综上所述,使用Fourier函数法描绘形态时,采样点的个数不宜少于60。使用Lagrange函数法时,可采取2种采点方式:第1种,可取少量采样点,但在各分段连接点附近应密集采点;第2种,可取较多的采样点,以此降低连接点附近的误差。对于Hermite和Spline函数法,可选择相对较少的采样点来描述实际形态,但不宜少于36。但是,在使用Hermite函数法时,需要量取采样点的导数值,相对于Spline法,采点的工作量较大。

2 黄土颗粒形态描绘

2.1 样本选取

黄土颗粒轮廓可分为光滑和棱角结构明显2类,为了检验上述函数法是否适用于黄土颗粒,从陇东正宁L1黄土土层中分别取了几个代表性土样。利用扫描电镜获得颗粒形态,再从中选取一个光滑、一个棱角结构明显的颗粒,如图4所示。注意只分析2个粗的骨架颗粒的轮廓,大颗粒表面分散一些细粒,不考虑其影响。其中颗粒1轮廓较为圆滑,颗粒2轮廓棱角结构明显。在采样点为120的情况下,利用4种函数法分别对颗粒1、颗粒2进行描绘,描绘结果如图5所示。

图4 选取的颗粒样本镜下照片Fig.4 Photos of the selected particle samples under the microscope

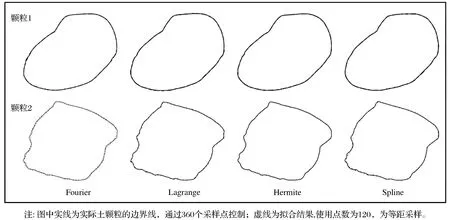
图5 各方法对真实土颗粒的描绘效果Fig.5 Effect of depicting real soil particles with each method

2.2 结果分析

(1) 形态分析 图5表明,对于颗粒1,4种函数法的描绘结果与原始颗粒的形态都较为接近,其中Fourier函数法的描绘结果在少部分区域内与原始结果略有差异。Fourier函数法的描绘结果与使用的Fourier函数的阶数密切相关,Fourier函数的阶数越高,描绘结果与原始结果越接近[21]。由于研究使用12项Fourier函数来描绘颗粒形态,因此描绘结果与原始颗粒略有差异,其余3种函数法的描绘结果在形态上无明显不同。对于颗粒2,Lagrange和Hermite函数法的描绘结果较好地体现了原始颗粒的棱角结构,Fourier和Spline函数法的描绘结果未能体现原始颗粒的部分棱角。由于Lagrange 函数法使用的Lagrange函数的各分段连接点为不可导点,这种不可导点能很好地体现颗粒表面的棱角形态。Hermite函数为带导数型插值函数,当各分段连接点处于棱角结构处时,由于各分段连接点处左右导数值不同,从而达到与Lagrange函数法相同的效果。在Fourier和Spline函数法描绘出的颗粒边界上,导数处处连续,这使得边界曲线较为光滑,但对于棱角结构明显的颗粒来说,棱角结构会被圆滑。这表明Lagrange和Hermite函数法比Fourier和Spline函数法更加适合描绘棱角分明的颗粒。

(2) 半径误差 在一些力学模拟中,需要精确控制颗粒接触位置,故在颗粒描绘中,必须保证控制点位置与拟合结果相同。在实际应用中,可将部分采样点作为控制点。图6展示了4种函数法在点数不同的情况下,颗粒1和颗粒2的拟合半径与实际半径的相对误差变化。

图6表明,Lagrange、Hermite、Spline函数法在采样点处的相对误差均为0,而Fourier函数法在采样点处均有误差。这表明除Fourier函数法,其他3种函数法都能有效通过采样点,这是由于研究使用Fourier函数的阶数有限造成的,而其他3种函数法均基于插值函数,故可保证描绘结果通过采样点。

随着采样点数的增加,各函数法的描绘结果在半径上产生的误差均有减小趋势。当点数增加到120时,对于颗粒1,Fourier函数法的描绘结果在半径上产生的误差相对于其他3种函数法较大,而其他3种函数法的描绘结果在半径上产生的误差在大部分位置都接近于0,这是由于Fourier函数法不过采样点造成的。对于颗粒2,各方法的描绘结果在半径上产生的误差变化情况基本与颗粒1类似。此外,Fourier和Spline函数法在195°～240°产生的误差相对于Lagrange和Hermite函数法较大,这是由于在该范围内,颗粒2棱角结构最为明显。从不同颗粒描绘结果的半径相对误差来看,各方法对颗粒1的描绘结果在半径上产生的误差要小于颗粒2。综上表明,4种函数法对圆滑颗粒的描绘能力优于对有棱角结构颗粒的描绘。此外,同形态分析结果一致,Lagrange和Hermite函数法比Fourier和Spline函数法更加适合描绘棱角分明的颗粒。

(3) 周长误差 考虑到颗粒边界凹凸不平,将边界分为360个微段,每1°为一段。周长(S)可表示为

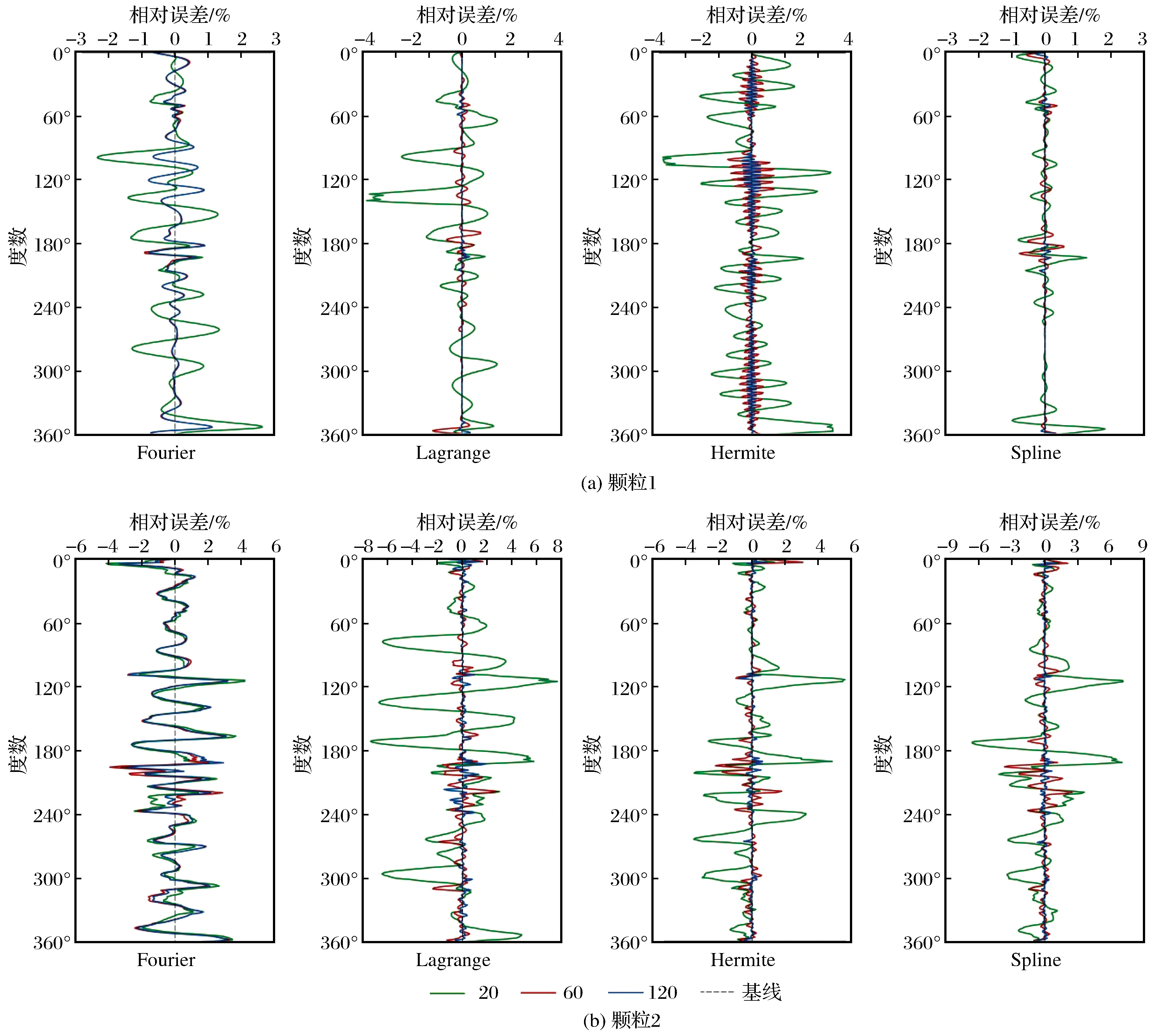
图6 真实土颗粒的拟合半径与实际半径的相对误差变化Fig.6 The relative error changing graph of real soly particles between the fitted radius and the actual radius

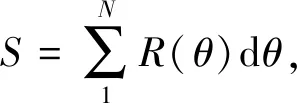
(8)

其中:N为微段总数,取360。

在采样点个数不同的情况下,4种函数法描绘结果的周长变化规律如图7所示。

图7表明,当采样点数较少时,周长的相对误差变化较大,这是由于采样点个数较少时,描绘结果的形态很难控制;随采样点数进一步增加,控制点逐步增多,周长逐渐趋于稳定。由于使用Fourier函数的阶数有限,这使得除Fourier函数法外,Lagrange、Hermite、Spline 3种函数法的描绘结果周长相对误差最终达到0。

图7 周长随采样点个数变化趋势Fig.7 Trend graph of perimeter with the number of sampling points

对于颗粒1,Spline和Hermite函数法描绘结果周长相对误差的变化规律基本一致,在采样点数较少的情况下,这2种函数法的相对误差也相对较小。对于颗粒2,Lagrange和Hermite函数法在采样点达到60时,这2种函数法的描绘结果在周长上产生的误差相对于其他2种方法较小。这表明,Lagrange和Hermite函数法比Fourier和Spline函数法更加适合描绘棱角分明的颗粒。此外,4种函数法对颗粒1的描绘结果在周长上产生的相对误差小于对颗粒2的描绘结果。同形态、半径误差分析的结果一致,即4种函数法对圆滑颗粒的描绘能力优于对有棱角结构颗粒的描绘能力。

3 结论

基于4种函数法对土颗粒描绘,结合形态分析、半径及周长误差分析,得出4种函数法的特点及其适用性:

(1) 在采样点合适的情况下,4种函数法都能有效地描绘颗粒形态。此外,相对于棱角结构明显的颗粒,4种函数法对圆滑颗粒的描绘能力较强。

(2) Fourier函数法所需要的采样点数要远多于其他3种描绘方法,描绘结果在形态上与原始颗粒较为接近,但其拟合结果不会通过采样点。Lagrange、Hermite、Spline函数法的拟合结果均通过采样点。

(3) 相对于Fourier和Spline函数法,Lagrange函数法更适合描绘棱角分明的颗粒。当在较少的采样点下使用Lagrange函数法时,各分段连接点附近需密集采点。

(4) Hermite函数法能描绘棱角分明的颗粒也可以描绘形态圆滑的颗粒。所需的采样点相对较少,但采点过程较为繁琐。

(5) Spline函数法对采样点的分布要求相对较低,采样过程简单。