三维坐标转换算法的粗差探测比较研究
蔡 宁,黄 腾,钱 龙,夏玉国
(1.河海大学地球科学与工程学院,江苏 南京 211100;2.中南大学地球科学与信息物理学院,湖南 长沙 410083)
大地测量坐标系的建立是大地测量学的基本任务之一[1]。新中国成立之后的几十年以来,我国先后建立了1954年北京坐标系、1980年国家大地坐标系和CGCS2000国家大地坐标系[2]。为了实现已有的测绘成果在各个坐标系之间的转换,高精度的转换参数必不可少。以最常见的布尔莎模型为例[3],该模型包括7个参数:3个平移参数、3个旋转参数以及1个尺度参数。至少需要知道2个坐标系下的3个公共点的坐标,才能求解出这7个参数。除了布尔莎模型外,另一种考虑到系数矩阵含有误差的模型(EIV模型)被认为是更加合理的[4-5]。不管是哪一种模型,当公共点坐标含有粗差时都会影响到转换参数的精度,为此如何探测粗差位置并将其剔除就成为研究的热点。常用的坐标转换算法主要有最小二乘(LS,least squares)和整体最小二乘(TLS,total least squares),整体最小二乘又可以分为奇异值分解(SVD,singular value decomposition)和混合最小二乘(LS-TLS)。研究将粗差引入到转换过程,通过方差比值检验法来比较LS、SVD和LS-TLS这3种算法的粗差探测能力,为后续的粗差剔除提供了参考。
1 三维坐标转换的参数解法
1.1 经典LS法求解坐标转换7参数
在线性布尔莎模型中,通常认为3个欧拉角是微小量,将旋转矩阵进行近似代替[6],模型可以简化为
(1)
(2)
其中:TX、TY、TZ、ωx、ωy、ωz、k为转换7参数。
只考虑观测向量L的随机误差,则误差方程为
L+VL=BX,
(3)
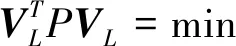
(4)
单位权中误差为
(5)
其中:n为公共点个数。
1.2 SVD解法求解坐标转换参数
式(3)矩阵B中的元素XS,YS,ZS也是有误差的,考虑到这一点可建立EIV模型[7],其函数模型为
L+VL=(B+eB)X,
(6)
其中:B∈R3k×t为系数矩阵;L∈R3k×1为观测向量;X∈Rt×1为所求7参数;VL是L的随机误差向量;eB是B的随机误差向量。
(7)
其中:U为左奇异阵;V为右奇异阵;∑是由特征值组成的对角阵;当vt+1,t+1≠0时,其唯一解为
(8)
单位权中误差为
(9)
1.3 LS-TLS解法求解坐标转换参数
LS-TLS解法将矩阵B的前3列元素视为常数项作为固定列,不做修正[8],所以需要将系数矩阵B分成B1和B2,X也对应分成的X1和X2。
LS-TLS解法先对不含误差的B1进行QR分解,再将Q左乘于增广矩阵[B,L],得到
(10)

2 方差比值检验法
方差比值检验法是吴祖海等[9]于2014年提出的一种新方法,它通过对最小二乘平差后的方差构建统计量来识别和定位粗差。它的原理和主要流程如下:
(1) 对于所有公共点,建立误差方程V(0)=BX-L。利用LS法求得转换参数,得到初始中误差σ(0)。
(2) 逐个删除公共点进行检验,在对第i个点检验时,将第i对公共点删除,构建不含第i对点的误差方程,计算此时的中误差σ(i)。

(11)
(12)
对于每一组公共点构造统计量[10]
(13)
Fi服从F分布,有
Fi~F1-α(r1,r2),
(14)
其中:α为显著性水平;r1、r2为自由度。对于参与平差的n对公共点,其自由度为r=3n-7。研究将方差比值检验法拓展应用到3种坐标算法上,通过分析Fi的大小来进行粗差的识别。
3 实例分析
为了比较3种算法的粗差探测能力,选取文献[11]中WGS-84坐标系和地方坐标系下的7个公共点(1~7号点),其在2个坐标系中的坐标见表1。分别编制3种算法的Matlab程序,实验时对4号点的X坐标分别加上1~10 cm的粗差,由于粗差不一定会使改正数V变大(见表2),因此需要使用方差比值检验法来验证,3种算法求得的Fi的结果见表3~表5。

表1 公共点在两坐标系下坐标
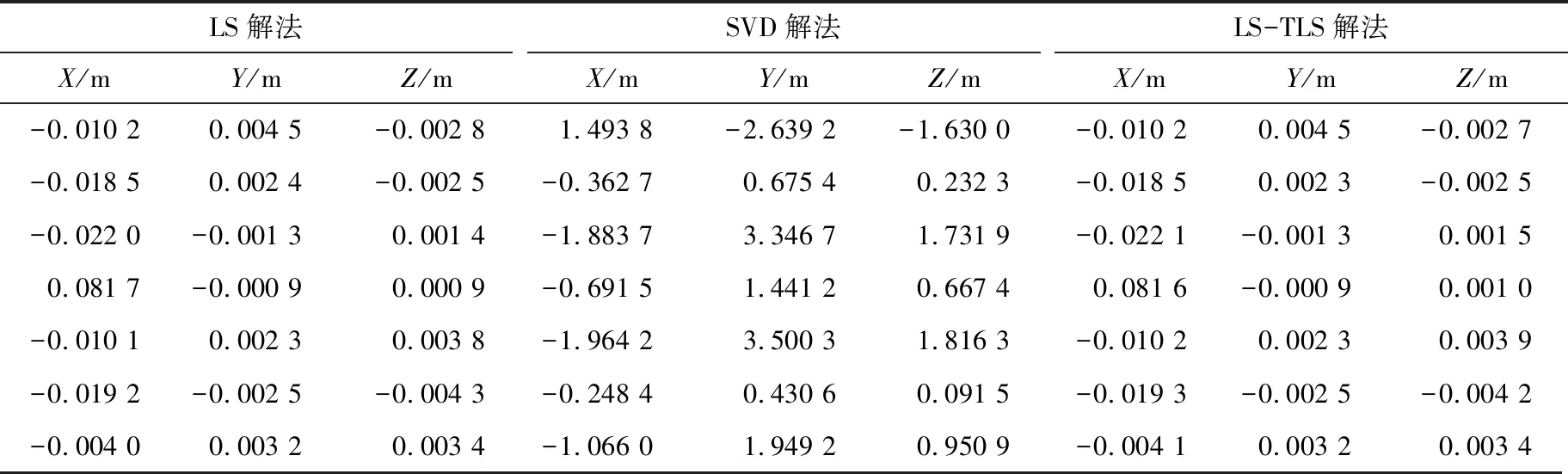
表2 4号点X坐标加10 cm粗差后的VTable 2 V of Point 4 X coordinates plus 10cm gross error
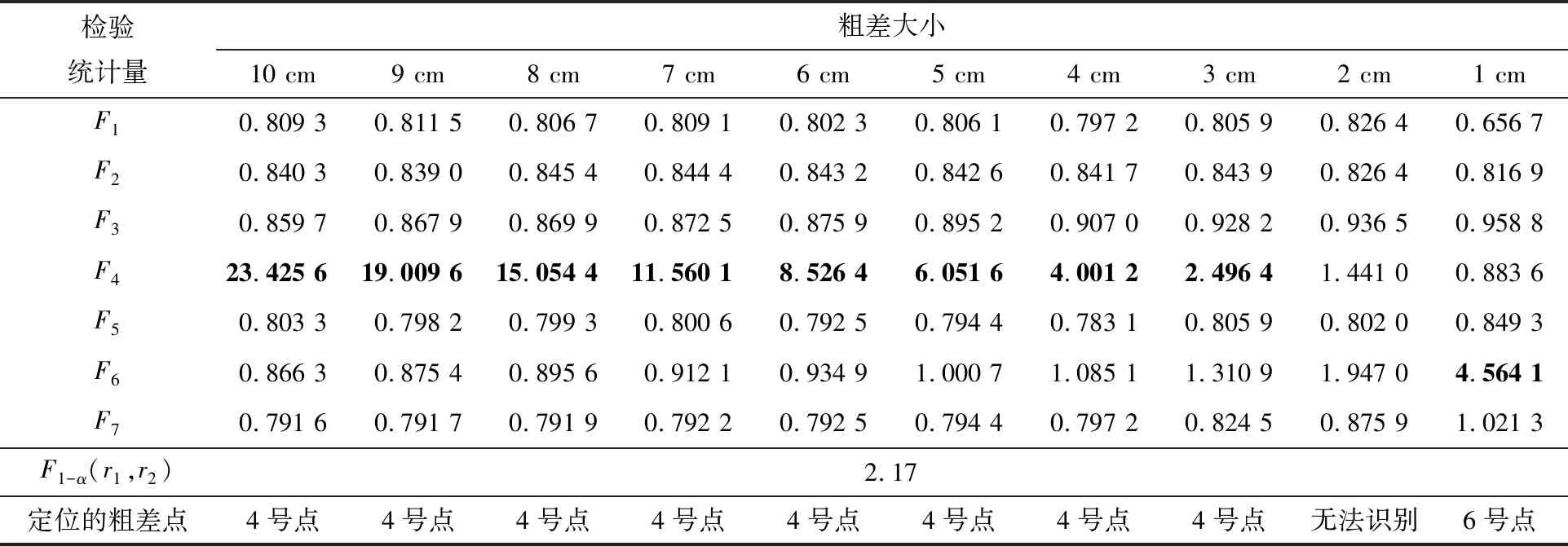
表3 LS法的方差比值统计量Table 3 Variance ratio statistics with the LS method
注:黑体数字表示大于检验指标。

表4 SVD法的方差比值统计量Table 4 Variance ratio statistics with the SVD method
注:黑体数字表示大于检验指标。
例中选取显著性水平α为0.1,即可信度为90%,通过查询分布表可知检验指标F0.9(14,11)=2.17,大于检验指标的组别被认为是粗差导致,即粗差位于该组。分析表中数据可知,LS和LS-TLS解法在粗差为3~10 cm的组中均能很好地识别粗差位于4号点,且粗差相同时LS-TLS求得的Fi均略大于LS的,即LS-TLS的粗差探测能力略好于LS,随着粗差的减小2种算法的粗差探测能力逐渐变弱;在粗差为1 cm和2 cm时,2种解法均会出现无法识别和识别错误的情况;SVD解法在粗差为6~10 cm的组中能准确定位粗差位置,在粗差为1~5 cm这几组会出现无法定位或者定位错误的情况。

表5 LS-TLS法的方差比值统计量Table 5 Variance ratio statistics with LS-TLS method
注:黑体数字表示大于检验指标。
综合实验结果可知,3种算法在粗差较大时均能准确探测粗差位置,探测能力为LS-TLS最好,LS次之,SVD较差;在粗差较小时SVD无法探测粗差,LS和LS-TLS仍可以准确探测;在粗差很小时,3种算法均无法准确探测粗差。
4 结语
在使用布尔莎模型或者EIV模型求解坐标转换7参数时,源目标坐标中如果含有粗差,会影响平差结果使得求出的参数解不正确,因此定位粗差位置并将其剔除就显得十分重要。研究使用方差比值检验法对3种转换解法的粗差探测能力进行了比较,结果表明LS和LS-TLS算法具有较好的粗差探测能力,而SVD解法的探测能力较差。值得注意的是,针对的原始坐标只有1组数据含有粗差的情况,对于多组数据均含有粗差的情况可能需要进行多次F检验。并且为了能更好地定位粗差,需要视情况灵活的改变α的值,对于多组数据同时含有粗差以及如何应对粗差较小的情况,将在后续的研究中进行。

