多摄站数码影像光束法相机检校的研究

谷晴晴,李 浩

(河海大学地球科学与工程学院,江苏 南京 211100)

近景摄影测量以其快捷和非接触的方式在工程、工业和建筑等多个领域得到了广泛的应用[1]。普通数码相机凭借其成本低、体积小、灵活方便等优势被广泛使用在实际的工程项目中,但它同时也存在着内方位元素不稳定、光学畸变差较大等缺陷,导致测量的像点坐标存在较大的误差,对摄影测量成果的精度产生了极大的影响[2-5]。因此需要通过相机检校技术获得相机的内方位元素和畸变系数,对影像进行校正,进而提高摄影测量工作的精度[6-8]。目前,基于精密三维控制场的光束法相机检校作为普通数码相机检校的一种经典方法,其数学模型成熟严密,得到的检校结果也较为精确稳定,并被广泛应用于普通数码相机的检校中。但由于它将所有的参数纳入同一个平差模型中进行解算,检校结果会受到参数间相关性的影响,如果物方控制条件不良,则可能会导致解算精度降低或解算不收敛。从理论上来说,增加影像数量可以改善平差的几何条件,减小内方位元素和外方位元素之间的相关性,从而增加未知参数的可测性。研究通过对室内三维控制场架设多个摄站进行拍摄,得到了多张不同拍摄角度的数码影像,然后利用不同数量的影像进行光束法相机检校,对检校结果从稳定性和量测应用精度2个角度进行了评价分析,并得出相关结论,为光束法相机检校在实际的应用中提供参考和帮助。

1 光束法相机检校原理

光线束检校方法是以共线条件方程式为基本数学模型,将像点坐标作为观测值,把内外方位元素、畸变参数、控制点的物方坐标等作为未知参数进行整体平差[9]。当考虑到构像畸变差时,其基本公式为

(1)

其中:(x,y)是像点坐标;(x0,y0)是像主点坐标;f是相机主距;(XS,YS,ZS)是像片的外方位线元素;ai,bi,ci(i=1,2,3)是由外方位角元素组成的方向余弦;(Δx,Δy)是系统误差,这里的系统误差指的是构像畸变差[10],考虑镜头的径向畸变和切向畸变,其校正模型为

(2)

(3)

其中:(x)、(y)为依据共线方程求得的各像片像点坐标的近似值。

假设拍摄了m张像片,有n个物方点,则每张像片可列像点坐标误差方程为2×n个,总共可列2×m×n个误差方程,则对2张或多张像片整体进行平差解算,可表示出以下误差方程:

第1张像片:v1=A1X1+B1X2+C1X3+D1X4-l1,

第2张像片:v2=A2X1+B2X2+C2X3+D2X4-l2,

第3张像片:v3=A3X1+B3X2+C3X3+D3X4-l3,

……

第m张像片:vm=AmX1+BmX2+CmX3+DmX4-lm,

其中:X1、X2、X3、X4分别为相机内方位元素改正数向量、像片外方位元素改正数向量、畸变系数改正数向量以及控制点和待定点物方空间坐标改正数向量。那么整体平差的误差方程表示为

v=AX1+BX2+CX3+DX4-l。

(4)

另外,在上述光束法平差过程中,对于控制点还需添加1组虚拟观测方程,以保证算法的有效进行,这样做有助于改善法方程系数矩阵的结构并促进算法的收敛[2]。添加的虚拟方程为

(5)

建立误差方程式后,根据最小二乘原理即可求得相机内方位元素、像片外方位元素、畸变参数以及物方空间坐标。

2 实验条件

实验使用的相机型号为FUJIFILMX-T10普通数码相机,分辨率为4 896×3 264,在拍摄照片时将摄影方式设置为手动曝光方式,物镜对焦在无穷远处,从而锁定主距,即锁定了内方位元素值和物镜畸变系数。实验以室内三维精密控制场为摄影对象,控制场框架结构的尺寸为3 600 mm×2 400 mm×2 000 mm。控制场沿摄影方向分为前、中、后3个层面,最前面1层的控制点个数为49个,后面2层均为35个控制点,如图1所示。

实验中架设了7个摄站拍摄三维控制场,共获得7张影像,7个摄站距离控制场第1层的平均距离约为2.9 m,摄站的分布情况如图2所示。

图1 室内精密三维控制场Fig.1 Indoor precision 3D controlling field

图2 摄站示意图Fig.2 Camera station map

首先在控制场的正前方架设S1站,拍摄时镜头正对着控制场,采取正直拍摄方式,即相机镜头无明显偏向左方或右方;然后在距S1站左边大概35 cm、70 cm和105 cm处分别架设S2、S3和S5站,为了保证把整个控制场放在像幅中间且避免过多的点被遮挡,S2、S3和S5站处的相机镜头相对于正直拍摄方向均稍稍偏向右前方,偏转的程度依次增大。同样地,在距S1站右边大概35 cm、70 cm和105 cm处分别架设S5、S6和S7站。根据拍摄的7个摄站影像,实验设计了3种方案用来验证影像数量和影像拍摄角度对光束法相机检校的影响,如表1所列。首先利用S1站、S2站和S5站拍摄的影像作为一个平差单元进行光束法解算,构成3张影像的光束法检校,然后加入S3站和S6站拍摄的影像构成5张影像的光束法检校,最后再加入S5站和S7站拍摄的影像构成7张影像的光束法检校,3种摄站方案的具体情况见表1。

表1 3种摄站方案

3 检校稳定性的比较

检校稳定性指的是当控制条件正常变动时解算出来的参数应该稳定[11],它是评价相机检校结果好坏的一个重要指标。

为了验证3种摄站方案的检校稳定性,根据所拍摄室内三维控制场中控制点的分布,给出了4种控制点组合:组合一是控制点共面的情况,选择了控制场第1层面上的23个控制点,它们基本处于同一平面,并且均匀分布;组合二和组合一的控制点数量相同,但前者利用了控制场3个层面上的23个控制点,它们均位于控制场的边角位置,在不同深度上数量相当,在同一平面上的分布均匀对称;组合三是控制点较多的情况,利用了控制场3个层面上的45个控制点,它们均位于控制场的边角位置,在不同深度上数量相当,在同一平面上的分布均匀对称;组合四属于控制点稠密的情况,利用了控制场中的88个控制点。4种控制点组合的情况见表2。

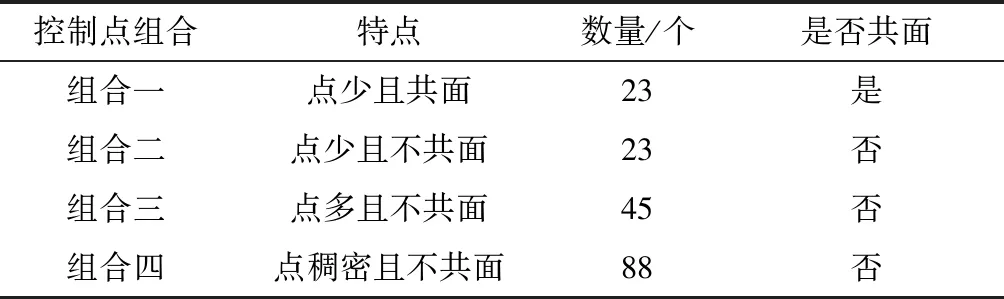
表2 4种控制点组合

在3种摄站方案下利用不同的控制点组合进行光束法检校得到的内方位元素见表3。

表3 3种摄站方案下的内方位元素

由表3可以看出,随着控制点个数的增加,解算出来的内方位元素逐渐达到稳定,但从整体上来看,方案2的检校结果波动最小,达到稳定的速度更快一些。3种方案下组合一和组合二之间f的偏差分别在22个像素、8个像素和26个像素左右,说明在控制点共面情况下检校结果较差,其中方案2的检校结果最稳定;而对于控制点不共面的组合二和组合三,3种方案下f的偏差分别在8个像素、5个像素、26个像素左右。同时也说明控制点的数量和分布对检校结果产生了较明显的影响,方案3波动尤为明显;对于控制条件良好的组合三和组合四来讲,方案1和方案3下检校结果的最大偏差分别在4个像素和7个像素左右,而方案2得到的最大偏差在2个像素左右,说明在控制条件良好情况下的检校结果较为稳定。

另外,方案2比方案1的检校稳定性要高(特别是在控制点共面的情况下),说明增加影像数量在一定程度上减小了内方位元素和外方位元素之间的相关性,提高检校参数的稳定性。而方案3与方案2相比,虽然又增加了2张影像,但检校稳定性却变差了,说明并不是检校影像数量越多,稳定性越高。由前面的摄站介绍可知,方案3在方案2基础上多加入的2张影像拍摄时相机镜头距离控制场中心较远,且镜头偏转的角度相对于其他的摄站更大一些,导致拍摄得到的影像并不利于检校,所以,尽管方案3的影像数量最多,但最后加入的2张影像并不利于检校,反而稳定性最差。方案2在方案1的基础上加入的影像虽然相对于正直拍摄方向也有所偏转,但偏转相对较小,且距离控制场中心相对较近,而影像数量的增加又减弱了解算元素之间的相关性,所以在方案1的基础上提高了稳定性。

4 量测应用精度的比较

在实际的应用中,往往先对普通数码相机进行检校得到它们的内方位元素和畸变系数,然后把相机作为量测相机使用,在处理摄影测量工作之前先利用相机参数对影像进行校正,然后利用摄影测量的后交-前交算法计算得到物方点位精度,即量测应用精度,它也是评价检校出来的相机参数好坏的一个重要指标。

为了验证3种摄站方案下得到的内方位元素的可靠性,实验在距离控制场左前方和右前方大概3.1 m 的位置分别拍摄了2个不同摄影基线长度的立体像对,其基线长度分别为0.9 m和2.8 m。实验中对这2个立体像对分别利用前面3种摄站方案下光束法解算出来的最佳相机参数进行像点坐标的校正,然后应用摄影测量后交-前交算法进行解算并求出坐标精度,物方坐标采用近景摄影测量坐标系,其X和Z方向分别沿水平和铅垂方向,Y方向与拍摄方向相同。左右立体像对下得到的检校结果见表4。

表4 2个立体像对的量测应用精度比较

由表4可知,从整体上来看,像对B得到的点位中误差比像对A的精度要高,这是因为像对B的基线长度比像对A长的多,前者是后者的3倍左右。2个像对在3种方案下得到的量测应用精度均有一定的差距,整体规律表现一致,方案3的精度最差,方案2的精度最高。同时再次说明了在一定范围内,多摄站影像的光束法检校结果有利于提高其量测应用精度,但并不是检校影像数量越多得到的检校参数精度越高,如果加入的影像并不利于检校,那么得到的检校参数质量也不会好,从而也会导致量测应用精度的降低。

5 结论

通过对室内精密三维控制场架设多个摄站进行拍摄,得到了多张不同拍摄角度的影像,然后利用不同数量的摄站影像进行光束法相机检校实验,并对检校参数从检校稳定性和量测应用精度2个角度进行评价分析,结果显示增加影像数量可以提高光束法检校的稳定性和量测应用精度,但并不是影像数量越多越好,随着所增加的影像在拍摄时距离控制场中心越来越远,且镜头相对于正直拍摄方向的偏转越来越大,光束法检校的稳定性和精度反而可能会降低,并且影像数量的增加也会造成检校计算量增大,所以并不实用。总之,在实际的应用中可以考虑在控制场的左前方、正前方和右前方等合适位置架设5个摄站,共拍摄5张影像进行光束法相机检校,从而来获取最佳的检校稳定性和量测应用精度。