相机畸变的混合模型迭代检校法
汪佳丽,王炜杰,马振玲
(上海海洋大学海洋科学学院,上海 201306)
相机检校是摄影测量[1-2]和计算机视觉界长期关注的问题,至今为止国内外提出了很多检校方法,但仍然很难找到一个既能方便地适用于各种场景,又能得到很高精度的相机检校方法[3]。传统的畸变校正方法主要是利用棋盘格网等检校板,根据检校模型计算畸变系数和影像的内外方位元素,从而进行影像校正[4]。对于相机的畸变校正,文献[5]提出了Australis模型,并认为其为最优经验模型,但是缺乏对模型适应性的定量性分析。文献[6]表明对于大多数计算机视觉的应用,可以忽略切向畸变,但是对于一些短焦距大视角的镜头畸变,其切向畸变和平面内畸变都偏大,因此大多数情况下并不适用。文献[7]在传统畸变模型和文献[8]模型的基础上提出了新的畸变模型,能够将数码相机的整体检校精度降低到0.5像素以下。但是其建立的模型复杂程度较高,未知数个数较多,不利于实现,稳健性较低。文献[9]在现有相机的检校模型基础上提出了迭代的相机检校思路,发现模型的迭代检校法能够进一步提高检校精度。综上所述,目前的非线性畸变检校模型主要是针对相机中存在的径向、偏心和平面内畸变,由于CCD成像平面存在不规则和不平性,往往并不能简单地通过模型检校系数进行校正[3],而且畸变模型的检校精度还有待提高。
本文首先通过理论证明了考虑径向、偏心和平面内3种畸变的检校模型优于考虑其中一种或两种畸变的检校模型;其次针对相机成像平面的不平性等问题,在考虑3种畸变的物理检校模型的基础上引入了数学检校模型(切比雪夫多项式[10-11]),并通过试验验证了两个模型交替混合迭代,能更好地提高检校精度;最后对运动相机GoPro Hero 5 Black的线性模式进行了检校试验,结果显示本文提出的物理检校模型和数学检校模型的混合迭代检校法能够更好地提高检校精度。
1 相机检校模型
1.1 物理检校模型
一般来说,非线性光学畸变主要有径向畸变,偏心畸变及平面内畸变[12-13]。经典的相机平面校正模型(物理检校模型)为
(1)
式中,k1、k2、k3为径向畸变系数;p1、p2为偏心畸变系数;b1、b2为像元大小不均匀的情况下x方向的比例因子和非正交性(线性畸变)的畸变系数;x、y为像点坐标;x0、y0为主点坐标;r为实际像点的径向距离。
为了仔细分析各种畸变的影响,本文定义了几种物理模型。〇号模型:不估算任何畸变系数;二号模型:只估算偏心畸变系数p1、p2;三号模型:只估算径向畸变系数k1、k2、k3;五号模型:同时估算径向畸变系数k1、k2、k3和偏心畸变系数p1、p2;七号模型:同时估算径向畸变系数k1、k2、k3,偏心畸变系数p1、p2,平面内畸变系数b1、b2。
1.2 数学检校模型
除了应用物理模型,本文尝试采用两维切比雪夫正交多项式,作为数学检校模型来进行检校。切比雪夫多项式具有收敛性、正交性和对称性的特点。正交的特点保证系数间不相关,理论上任何模型都可以用一组n阶正交多项式来无限逼近[14]。根据魏尔施特拉斯逼近定理,闭区间的任何连续函数都可以用多项式级数逼近,本文采用一组第1类切比雪夫多项式来逼近影像畸变模型。切比雪夫多项式由式(2)的递推关系确定
T0(x)=cos 0=1,T1(x)=x,Tn+1(x)=2xTn(x)-Tn-1(x)
(2)
式中最高次xn项的系数为2n-1。式(2)为一维形式的切比雪夫多项式,两维形式的切比雪夫多项式检校模型为
(3)
正交多项式的阶数决定需要估算的系数个数,如采用3阶(M=N=3),即各用9个系数(am,n,bm,n)来描述x与y方向的畸变,本文切比雪夫多项式检校模型简称CHEBY模型。
2 相机检校试验及结果分析
2.1 考虑不同畸变系数的检校模型比较
针对物理检校模型是否应该考虑径向、偏心和平面内3种畸变还是考虑其中的一种或两种畸变的理论证明,本文模拟4张理想的棋盘影像,理想影像除去了噪声、光线等环境误差及控制点的量测等误差。此时理想影像的像方中误差和控制点空间坐标中误差都为0,通过模拟4组不同的畸变系数,对理想影像重采样得到4组具有不同畸变的模拟影像。4组畸变系数见表1。
针对4组模拟影像,分别使用不同的物理检校模型进行检校,检校精度如图1所示。
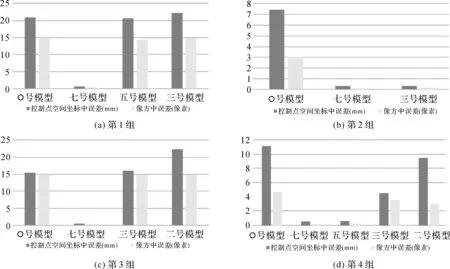
图1 不同物理检校模型对模拟影像的检校结果比较
从图1可以看出,对应于4组具有不同畸变的模拟影像,考虑径向、偏心和平面内3种畸变的7号模型检校精度最高。
2.2 模拟影像的混合模型迭代检校试验
文献[15]提出对于相机表面存在的不平性等制造误差可以通过径向畸变和有限元内插畸变两部分进行消除。本文在先前提出的迭代检校法基础上引入了数学检校模型,在迭代过程中交替使用物理检校模型和数学检校模型,从而形成混合模型的相机迭代检校法。
首先利用表1中的第1组畸变系数获取的4张畸变模拟影像试验,针对混合模型迭代检校是先采用物理检校模型(七号模型)还是先采用数学检校模型的问题进行了探讨。假设模拟影像的外方位元素未知,分别对该4张模拟影像进行七号模型检校和CHEBY模型检校,检校结果发现CHEBY模型检校得到的外方位元素偏离真值较大,而七号模型检校的结果接近真实值,因此在外方位元素未知的情况下,混合模型迭代检校法先采用七号模型进行检校。
根据检校迭代思路,本文设计了两种迭代途径:迭代途径1是先采用七号模型迭代检校,当检校稳定后,固定外方位元素再采用CHEBY模型迭代检校;迭代途径2是先采用七号模型检校,固定外方位元素采用CHEBY模型检校,然后再采用七号模型检校,固定外方位元素后再次采用CHEBY模型检校,依次类推交错迭代检校,直至稳定。迭代途径一和迭代途径二得到的结果分别见表2和表3。
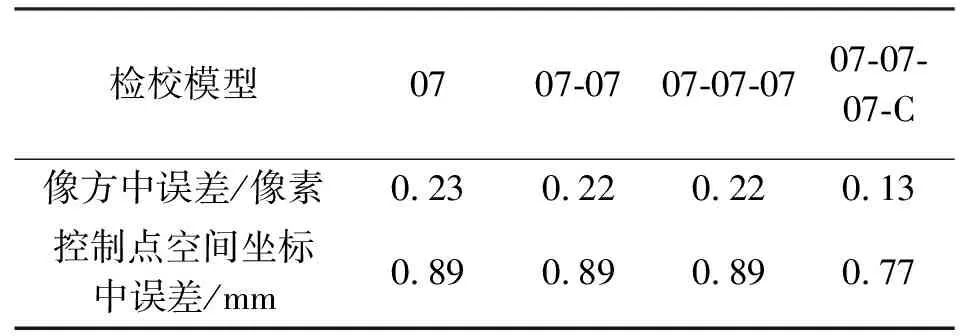
表2 迭代途径1检校结果
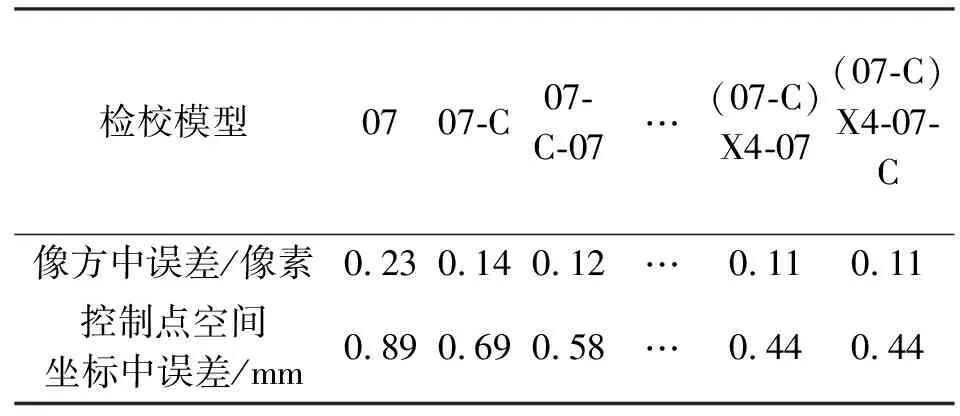
表3 迭代途径2检校结果
表中07表示七号模型一次迭代检校;07-07表示七号模型的二次迭代检校;07-C表示先采用七号模型检校,然后固定外方位元素数进行CHEBY模型检校;07-C-07表示采用七号模型和CHEBY模型检校后再采用七号模型检校;(07-C)X4表示4次七号模型和CHEBY模型检校混合交错迭代。其他检校迭代标号表达以此类推。
比较两种迭代检校途径结果可以发现,迭代途径2小于迭代途径1,即交替采用七号模型与CHEBY模型的混合模型迭代检校途径优于先采用七号模型迭代检校再采用CHEBY模型迭代检校的混合模型迭代检校途径。
2.3 GoPro Hero 5 Black运动相机的混合模型迭代检校试验
本文利用GoPro Hero 5 Black相机的线性模式进行了混合模型的迭代检校试验。该款相机拍摄的影像具有1200万像素分辨率,传感器尺寸为1/2.3英寸,焦距约为3.4 mm。选用具有规则几何形状且砖块纹路清晰的建筑物墙面作为检校场,在距离墙面约1.1 m处拍摄7张影像,设置了71个控制点,利用全站仪获取的控制点量测精度约为2 mm,影像的像素分辨率约为0.46 mm。通过七号模型和CHEBY模型进行混合迭代检校7次后控制点空间坐标中误差和像方中误差趋于稳定,此时像方中误差约为1.91像素(相当于平面0.88 mm),物方空间坐标中误差约为2.00 mm,检校精度见表4。

表4 GoPro Hero 5 Black相机混合模型迭代检校精度
3 结 语
本文首先通过模拟影像引入各种畸变,然后对其进行畸变恢复检校试验,试验证明考虑径向、偏心和平面内3种畸变的物理检校模型比只考虑一种或两种畸变的物理检校模型能更好地对影像进行畸变检校。针对现有物理检校模型不能完全消除影像残余畸变的情況,本文引入了数学检校模型(切比雪夫多项式检校模型),并通过模拟的畸变影像验证了交替采用物理检校模型和数学检校模型的混合迭代检校能获得更优的检校效果。最后对运动相机获取的真实影像进行进一步试验,结果表明基于混合模型的迭代检校法能进一步提高检校精度。今后将进行把主距主点作为检校参数纳入相机检校模型的研究。

