轨迹压缩的典型方法评价

梁 明，陈文静，段 平，李 佳

(1. 安徽大学资源与环境工程学院，安徽 合肥 230601； 2. 云南师范大学旅游与地理科学学院，云南 昆明 650500)

轨迹数据是典型的时空大数据，其在多个领域都有着极其突出而重要的研究和应用价值[1-2]。作为时序数据的特例，轨迹数据具有鲜明的时序特征，同时还具有突出的空间特征。因此，轨迹数据的处理和挖掘方法不能完全照搬时序数据的经验，而应当考虑其特殊性。当前限制轨迹数据处理和挖掘的重要因素之一是轨迹数据海量的数据规模[3-4]。轨迹数据的海量数据规模带来的问题是多方面的，主要表现在：①数据存储压力大，海量的数据规模和非结构化的数据组织为轨迹数据的实时数据存储和快速索引带来了巨大的挑战；②数据的分析压力大，典型的数据挖掘方法在面对海量轨迹数据时通常无法直接使用，为轨迹数据的分析和挖掘带来了挑战；③轨迹数据的可视化压力大，可视化是轨迹数据理解和分析的重要手段，而海量的数据规模让传统的可视化手段无用武之地，特别是面向Web端和移动端的实时可视化时更显得传统手段的不足。

针对轨迹这类特殊时空数据的压缩方法的研究已经成为轨迹大数据研究领域的重要研究内容。轨迹压缩的实质是实现轨迹的数据规模和数据质量的统一，即数据的“量”与“质”的统一。正是由于轨迹数据不同于常规的时序数据，它有着丰富多维的时空特征，因而在轨迹数据压缩的过程中，如何在减少数据量的同时尽可能保障轨迹数据的多维时空特征的损失最小，是不同轨迹压缩方法都应该考虑的问题[4-5]。现有轨迹压缩方法的研究虽多，但是缺乏对轨迹数据在各个维度的时空特征损失的评价研究。因此，本文综合选取了MBR面积误差、距离误差、方向误差等多个指标[6]，分别从几何形态和运动特征等多个角度对典型的轨迹压缩算法进行评价，从而为轨迹压缩的研究和实际应用提供更精确的量化参考。

1 典型轨迹压缩方法

轨迹压缩方法可以分为不同的类型，根据轨迹压缩过程中是否参考地理背景，可以将轨迹压缩分为两种类型：一种是仅仅基于轨迹几何线划特征的压缩方法；另一种是基于路网或语义的轨迹压缩[7-8]。此外，由于轨迹压缩过程中最重要的是要寻找最典型最有代表性的特征点，因而基于选取特征点方法的不同，又可以将轨迹压缩方法分为基于全局特征的轨迹压缩方法和基于局部特征的压缩方法。基于全局的压缩方法，如经典的Douglas-Peucker(简称DP)算法，它是基于特征点到全局的首末节点连线的欧氏距离进行特征度量的方法[9]；依时间比例的自顶向下算法(top-down time ratio，TD_TR)同样是基于全局特征的，但是不同于DP算法直接采用欧氏距离作为压缩阈值，TD_TR算法采用时间同步欧氏距离作为压缩阈值[10]。此类全局压缩算法优点在于在考察轨迹点的特征时是从全局出发进行度量的，能够保留轨迹数据的整体形态。然而，由于此类全局算法通常是递归的，因此压缩速度较慢。此外，DP和TD_TR算法无法有效压缩封闭的或者起止点相邻过于接近的轨迹。

全局压缩算法适用于静态或历史的轨迹数据压缩。对于实时在线的轨迹压缩需求，基于局部特征的压缩方法更为合适。最简单的局部压缩算法，只需要考虑当前点和相邻两个节点之间的特征关系，如垂距法和夹角法等，但是由于比较的对象过少，此类压缩算法无法甄别出局部变化小而累积起来变化大的时空弯曲[11]。因此，相对而言基于窗口的压缩算法能够更好地统筹局部特征和整体特征。典型的窗口压缩算法有滑动窗口算法(slide window，SW)和开放窗口算法(opening window)[12]，其中开放窗口算法又因选取终点的策略不同而分为一般开放窗口算法(normal opening window，NOPW)和向前开放窗口算法(before opening window，BOPW)。窗口算法是通过在窗口不断更新窗口完成轨迹压缩，而STTrace和SQUISH算法则是通过提供一个缓冲区，通过控制缓冲区的大小来控制给定压缩率的情况下实现轨迹压缩的[9,13]。因此，除了STTrace和SQUISH压缩算法以外，其他的轨迹压缩算法都可以基于给定的空间阈值进行压缩(距离或角度等)。

2 轨迹压缩方法的评价指标

对轨迹数据进行压缩会带来轨迹多维时空特征在不同维度上的损失。虽然部分研究对轨迹压缩在某些维度的时空特征损失进行了探讨，但是一方面这些研究分析的特征维度少，另一方面相关研究缺乏系统的对比研究。因此，本文从轨迹数据的几何特征、运动特征和压缩效率等3个角度，分别选取MBR面积误差、方向误差、距离误差、速度误差、压缩率及压缩速度等6个指标对轨迹压缩方法进行系统的对比分析。

同时，为了综合分析轨迹数据压缩算法在多个压缩尺度上误差损失的一致性，本文选取了多个尺度进行分析。由于各类算法在具体实现上有所差异，尺度选择又可以分为两种不同的类型：一种是通过距离阈值来度量的空间尺度，另一种是以压缩率为阈值度量的效率尺度。其中本文对DP、TD_TR、SW、BOPW、NOPW等采用基于距离阈值的多尺度评价方法，以距离阈值作为空间尺度变化进行评估，而对SQUISH、STTrace则以压缩率作为尺度阈值进行评估。

轨迹压缩对轨迹数据质量的影响首先体现在轨迹几何形态上。MBR作为轨迹几何的最小外包矩形，对于度量轨迹形态变化具有重要的意义。MBR面积误差，即为原始轨迹MBR的面积(通过比较相邻特征点之间的轨迹点，找到轨迹对应的4个极值点)与压缩后轨迹的MBR之间面积的差值。该指标用于分析轨迹数据压缩前后几何形态上的变化程度。通常认为，面积误差越大，则轨迹在压缩前后的几何形态损失越大。

(1)

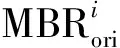
在几何形态误差度量中，另一种典型方法是度量压缩前后轨迹特征点的距离误差[14-15]。距离误差，即首先在压缩后的轨迹上重建被省略的冗余点位置，然后计算压缩前后对应两点之间的距离误差的总和，并将其总和值除以原始轨迹的总点数。作为典型的轨迹压缩评价方法，距离误差能够较好地表达轨迹形态在压缩前后的变化。

(2)

轨迹数据中隐含了轨迹的运动特征，运动特征是轨迹数据不同于常规时序数据的显著特征。由于运动特征对于轨迹挖掘具有举足轻重的意义，因此，如何确保轨迹压缩时对运动特征的损失最小，是轨迹压缩方法评价的重要内容。方向和速度作为轨迹数据关键的运动特征，尤为值得重视。

方向误差是将压缩轨迹的方向直接使用两点之间的方向(以正北方向为正方向，以顺时针方向进行度量)对压缩后的轨迹进行重建，即计算出冗余点在压缩后的轨迹上的时间同步点，然后一一对应的计算点之间的方向差值，以绝对值累加，最后除以总点数。该指标同样用于评估轨迹数据压缩前后几何形态的变化，不过侧重在轨迹压缩前后的方向上。

(3)

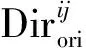
速度误差是对压缩后的轨迹进行重建，即计算出冗余点在压缩后的轨迹上的时间同步点，然后一一对应计算点之间的速度差值，以绝对值累加，最后除以原始轨迹点的总点数。该指标也是用来评估轨迹压缩前后运动特征损失的重要指标之一。

(4)

压缩率即使用压缩后点的个数除以原始轨迹点的个数。压缩率越小则说明压缩后保留的轨迹点越少。对于SQUISH、STTrace两种轨迹压缩方法，由于它们是基于缓冲区的压缩方法，不宜选用距离作为尺度度量。因此，本文选取给定压缩率的方式来度量不同压缩率下SQUISH和STTrace两种压缩方法对轨迹数据时空特征的影响。

CR=Ncom/Nori

(5)

式中，Ncom为压缩后的轨迹点数；Nori为原始轨迹的轨迹点数。

压缩速度即使用压缩所用的时间除以原始轨迹的总点数。用压缩速度来分析度量不同轨迹压缩算法的压缩效率。以压缩速度为指标系统分析轨迹压缩效率在多个不同压缩尺度上的性能差异，从而为轨迹压缩算法的选择和压缩阈值确定提供参考。

3 评价结果与分析

本文选用微软亚洲研究院的GeoLife数据集作压缩试验的数据(https:∥www.microsoft.com/en-us/download/details.aspx?id=52367)。该数据集收集了北京地区178位志愿者2007—2011年的时空轨迹采样数据。GeoLife数据集共包含17 621条记录，记录了超过1.25×106km的轨迹距离。由于数据的典型性和丰富性，GeoLife数据集已经被广泛应用于轨迹数据研究的众多领域。由于GeoLife数据在采样过程中存在一定的误差和噪声，本文先用时间和空间约束对原始GeoLife数据集进行预处理。在针对本文目标的试验中，本文研究选择了多人的多条轨迹进行定量的度量分析。此处只列举了用户000的轨迹压缩和轨迹误差定量分析结果。

由上述压缩算法对多维运动特征影响的定量分析可见，在以距离为尺度阈值的压缩算法中，DP算法和TD_TR算法是对完整的轨迹进行压缩，考虑的是整体情况；而SW、BOPW、NOPW则是对局部的轨迹进行特征分析，并开展轨迹压缩。通过对MBR面积误差进行分析时可以看出(如图1、图2所示)，由于TD_TR算法使用距离阈值考虑了时间因素的时间同步欧氏距离，同时TD_TR又是全局算法，从而能够尽可能地保持压缩后轨迹的最佳形态，因此TD_TR压缩算法的MBR误差最小。对比分析NOPW和DP算法可以发现，NOPW算法虽是局部算法，但是并没有规定具体的窗口范围，而是由轨迹的形态决定窗口大小，相对地DP算法虽是全局算法，但在轨迹段的处理上并不细致，因此NOPW算法在形态保持方面略胜于DP算法。BOPW由于选取的不是窗口中距离代价最大的点，所以在保持上形态不及BOPW算法和DP算法。SW算法是局部算法，而且窗口的大小人为设置，一旦设置就不能改变，因此保留的点可能并不是信息量较多的点。

图1 以距离为尺度阈值的MBR面积误差

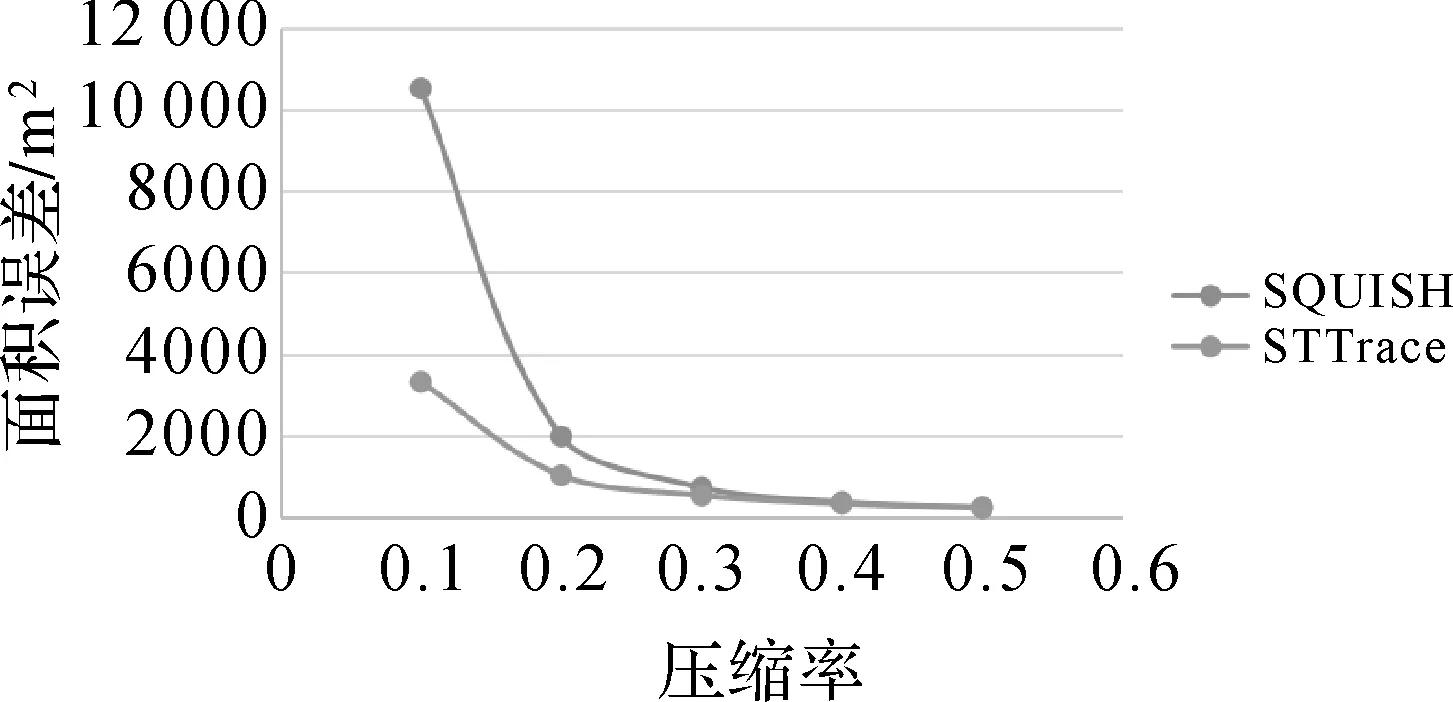
图2 以压缩率为尺度阈值的MBR面积误差

对方向误差的评价，是通过比较压缩后的轨迹的平均方向与压缩前轨迹的平均方向之间的误差进行的。当某个压缩算法保留的特征点越多、保留的特征点越重要，则其压缩前后的方向误差就越小。因此TD_TR算法的角度误差最小，剩余的算法误差与比较MBR误差时相似(如图3、图4所示)。而总体趋势上，随着压缩算法的空间尺度越大，各个算法都呈现出方向误差单调增加的趋势。

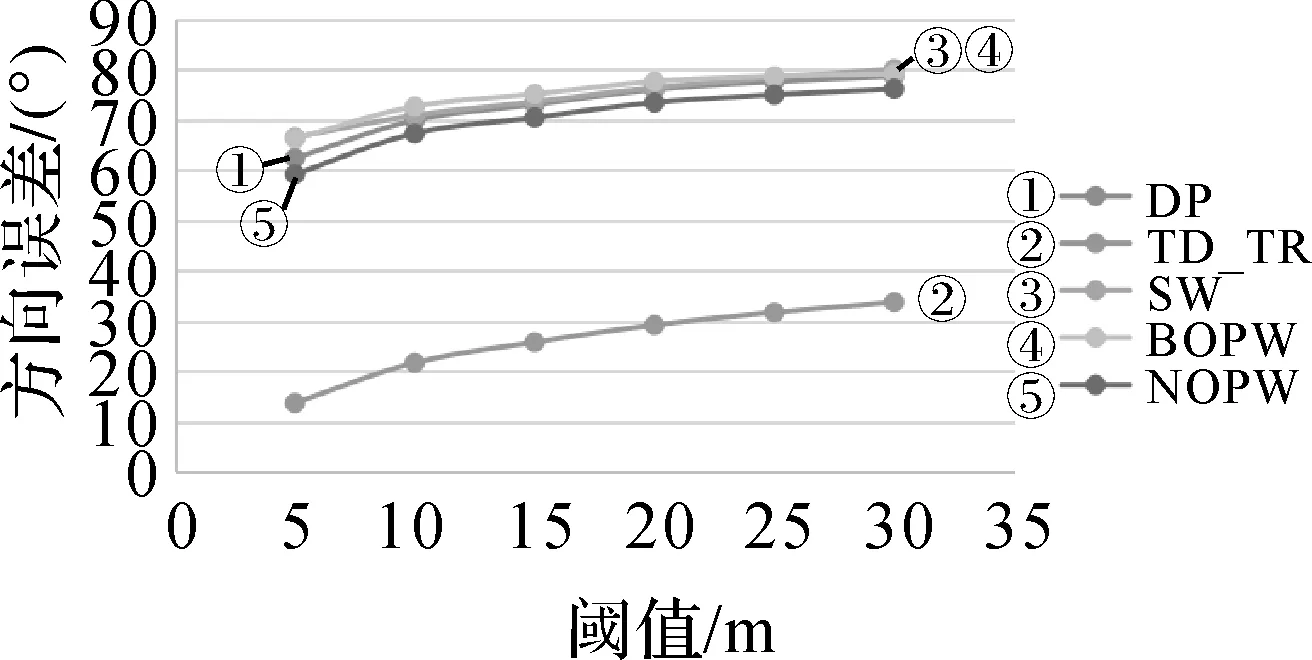
图3 以距离为尺度阈值的方向误差

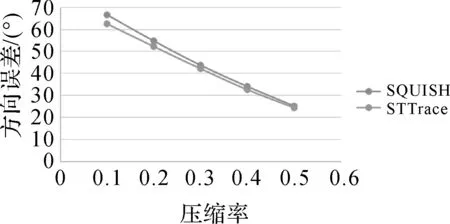
图4 以压缩率为尺度阈值的方向误差

距离误差评价与MBR误差分析相似，也是对形态保持方面的研究。因此得到的结果(如图5、图6所示)与MBR面积误差和方向误差评价的结论相类似。首先，TD_TR算法具有明显优于其他算法的最小距离误差，而SW滑动窗口算法具有较大的误差。其次，在多个压缩尺度上，随着空间尺度的增加各压缩算法造成的轨迹距离误差的趋势为单调递增。

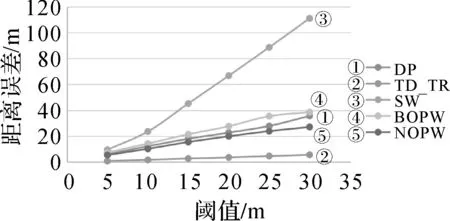
图5 以距离为尺度阈值的距离误差

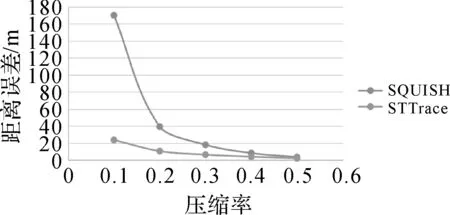
图6 以压缩率为尺度阈值的距离误差

对速度误差进行评价，是通过比较压缩后的轨迹速度与压缩前的轨迹平均速度之间的误差开展的。在总体趋势上其误差的分布结果与距离误差等类似(如图7、图8所示)。比较明显的变化是，在速度误差上，SW滑动窗口算法不再表现为随着尺度的增加误差相较于其他算法差距越大的趋势(图7)。其速度误差总体上呈线性增长。

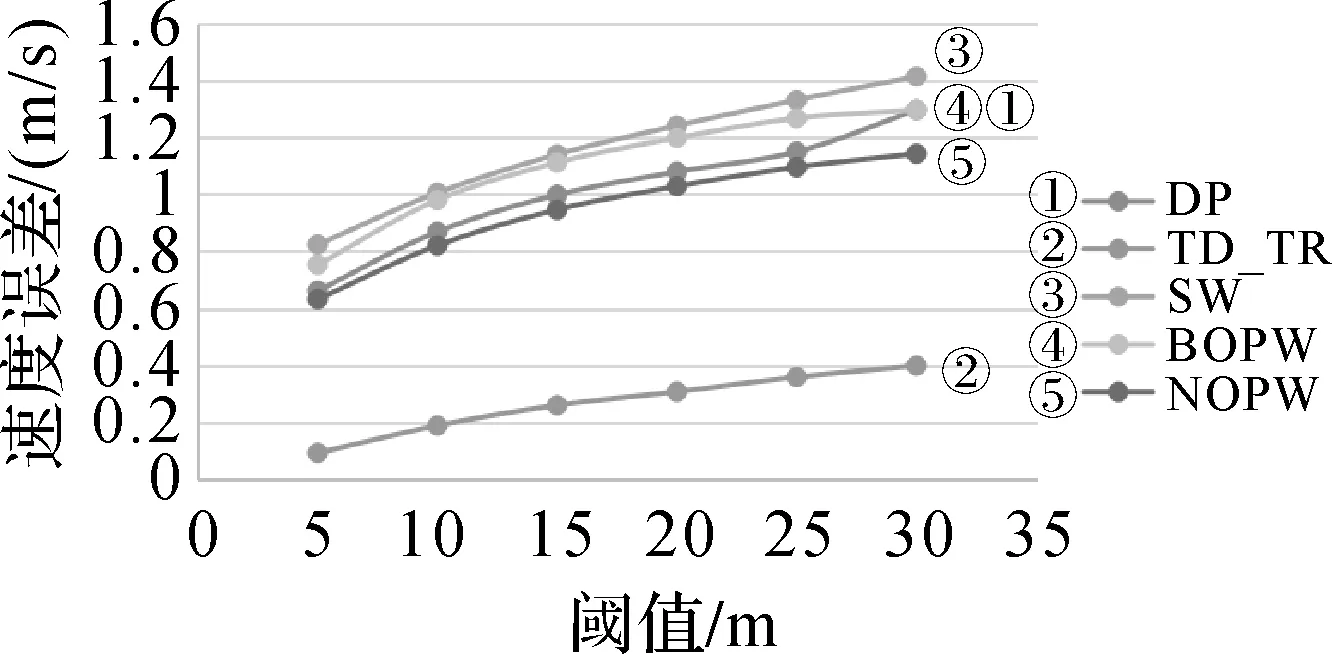
图7 以距离为尺度阈值的速度误差

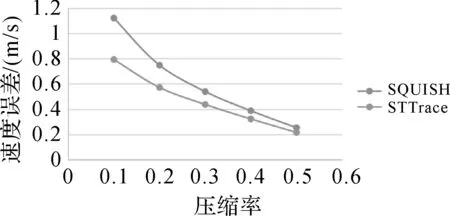
图8 以压缩率为尺度阈值的速度误差

针对压缩率的评价，在轨迹点特征度量时采用的点到线段的最短距离是垂直距离，因此轨迹点的垂直距离(ED)是大于时间同步欧氏距离的(SED)。在进行轨迹点的保留时若采用相同的距离阈值，那么使用时间同步欧氏距离算法保留的点会多于使用垂直距离的算法，因此TD_TR算法的压缩率最大及保留的点数最多。其余算法的压缩率相似，但仍有微小的差距，如图9—图11所示。

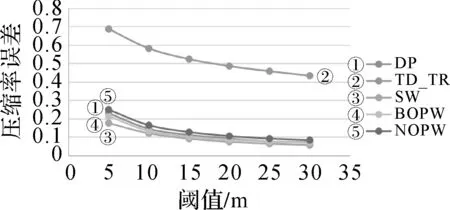
图9 以距离为尺度阈值的压缩率误差

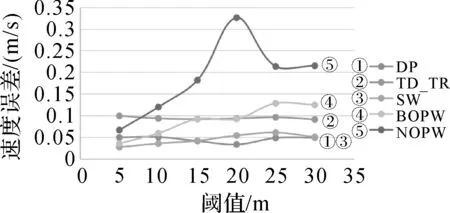
图10 以距离为尺度阈值的压缩速度误差

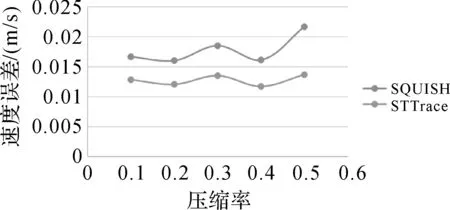
图11 以压缩率为尺度阈值的压缩速度误差

STTrace和SQUISH算法的思路大致相同，只是在更新冗余点前后对两个邻居点的时间同步欧氏距离的度量上有所差异：STTrace算法利用修改后的轨迹进行重新计算，而SQUISH是将冗余点的时间同步欧氏距离加到邻居点上。因此STTrace所求的每个点的时间同步欧氏距离是真实值，而SQUISH求得轨迹点的距离值可能因为累加导致的权重过大。因此在MBR误差、角度误差、距离误差、速度误差方面STTrace要优于SQUISH。

4 结 论

现有的各类轨迹压缩算法，无法完全兼顾轨迹数据在不同维度时空特征的保持。因此，不同的算法或以速度保持为优先、或以方向误差最小为目标。这些轨迹压缩算法虽有侧重，却缺乏各自算法对轨迹压缩各个维度时空特征损失的系统评价，无法为不同应用场景下轨迹压缩算法的选择提供定量的参考。因此，本文选取MBR面积误差、距离误差、方向误差、速度误差、压缩率和压缩速度等轨迹数据压缩前后的多维度时空特征，分别从轨迹的几何特征、运动特征和压缩效率3个方向对典型轨迹压缩方法进行评价。通过综合评价发现：①在特征度量中引入时间同步距离等顾及时空特征的压缩算法，如TD_TR算法，总体上能够较好地保持轨迹的时空特征；②不同压缩算法对轨迹数据时空特征的影响在各个尺度上的表现基本是一致的。虽然不同的数据集可能在量化误差时在具体分值上有差异，但是总体趋势应该是稳定的。总体上，研究表明难以有一种轨迹压缩算法能够兼顾所有维度时空特征的损失。本文的定量分析为具体应用中对轨迹压缩算法的选择提供了参考。然而，本文研究仅仅关注了轨迹压缩算法对单一轨迹本身多维特征的影响，而未考虑不同压缩算法对轨迹之间时空关系的影响。轨迹间的时空关系是时空检索和时空挖掘的基础。因此，在后续研究中应当进一步对典型轨迹压缩算法对轨迹间时空关系的影响开展定量研究。