基于投影变换的线阵旋转扫描相机标定方法

苏 琳，巫兆聪，闫 钊，王 鹏

(武汉大学遥感信息工程学院，湖北 武汉 430079)

线阵相机是指具有一列光学传感器的成像装置，通过扫描线的移动来获取二维图像[1]。基于该特点，线阵相机被广泛应用于机器视觉领域和卫星遥感领域[2-5]。

基于旋转运动平台的动态相机几何标定方法，目前对于此类问题的研究成果较少。基于旋转运动平台的线阵相机通常都只是用于纯粹的成像目的，但同时它在高精度测量、三维重建等方面具有很大的应用潜力[6]。目前，有研究人员根据旋转扫描线阵相机成像特点，建立了适用于旋转平台的线阵相机成像模型[7-8]，该模型在理想成像模型的基础上考虑了较多误差项，使得模型变得比较复杂，从而增加了模型解算的难度，而且具体的精度有待验证。

针对上述问题，本文拟构建一种基于投影变换的线阵旋转扫描相机成像模型，并提出标定方法，该方法简单灵活，只需要较少的标定数据就能进行相机标定，并且能得到精度较高的结果。

1 几何成像模型

为了方便成像模型的推导，首先进行以下定义：

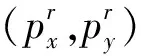
(1)

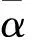
根据旋转扫描线阵相机的成像特点，α的计算公式为

(2)

设每个像素的大小为d，其计算公式为

(3)

如图1所示，G点表示框幅式图像的像主点，其对应的原始扫描图像的px列扫描线，则角β1和β2的计算公式分别为

(4)

图1 投影变换原理

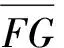
(5)

因此投影变换后图像的宽度计算公式为

(6)

(7)

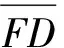
(8)

因此投影变换后图像高度的计算公式为

(9)

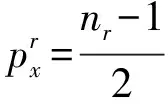
(10)

投影变换后坐标的计算公式为

(11)

则逆投影变换公式为

(12)

2 相机标定方法

投影变换后得到的框幅式图像的成像几何符合摄影几何约束，即三维空间中的点(X，Y，Z)与其投影到框幅式图像上的像点(xf,yf)满足以下公式

(13)

转换为直接线性变换公式为

(14)

因此将空间点投影到图像上的残差计算公式为

(15)

如果考虑旋转扫描成像时获取的参数为准确值，即扫描线夹角α已知，那么上述方程退化为标准的框幅式相机成像模型[9]，可以使用直线线性变换(DLT)方法[10]进行求解。

但在实际应用中，旋转扫描平台所给定的相邻扫描线夹角α与实际值有偏差，如果使用系统给定的值进行相机标定，标定结果会不准确。因此标定应该分为两步，首先是利用系统给定的α角作为初值，采用直接线性变换的方法求出相机参数初始值，再以像点坐标的重投影误差作为目标函数优化相机参数和α角，优化方法为Levenberg-Marquardt算法[11]。

3 试验及结果分析

试验采用线阵相机结合旋转平台从三维控制场获取标定数据。如图2、图3所示。

图2 原始三维控制场图像

图3 投影变换后的控制场图像

利用人工提取标志点的方法进行图像标志点的提出，共提取到53个标志点。然后采用DLT方法进行相机标定，利用标定参数计算得到的重投影误差为0.99个像素，表1为重投影误差。

表1 重投影误差 像素

考虑系统给定的相邻像素间的夹角α不准确会影响相机标定的结果，因此利用DLT所求得的结果和系统给定的α角进行非线性优化，优化结果见表2。

表2 α角优化结果 (°)

利用优化后的参数进行重投影误差计算，计算结果见表3。

表3 优化后的重投影误差 像素

对比表1和表3的结果可知，利用优化后的α角和相机参数所计算出的重投影各项误差均有明显减小，证明了优化方法的可行性和有效性。

从标定结果可知，本文标定方法所得出的标定结果误差小于1个像素，可见本文方法精度较高。试验结果证明了投影变换关系的准确性，也说明了利用投影变换的方法进行旋转扫描线阵相机标定的可行性。

4 结 语

本文提出了一种基于投影变换的线阵旋转扫描相机成像模型和标定方法，解决了现有的旋转扫描线阵相机成像模型参数较多、解算复杂且标定结果精度不高的问题，从而拓宽了旋转扫描线阵图像的应用领域。试验结果表明，相机标定的点位精度小于1个像素，能满足三维重建的要求。