桥梁转体施工球铰竖转摩阻力矩精确计算方法
罗力军
(1.中铁大桥科学研究院有限公司,湖北武汉 430034;2.桥梁结构健康与安全国家重点实验室,湖北武汉 430034)
随着国家基础建设的大力投资和交通网络建设的基本完善,越来越多的新建桥梁需要跨越运营线路,特别是跨越运营铁路和高速公路。为了不影响运营线路的正常运营,采用平转施工方法的桥梁越来越多,显示了较好的社会效益和经济效益[1]。
桥梁在转体过程中的平衡控制是关键,既要保证梁体在转体过程中的结构安全,又要保证梁体在转体过程中的可控性。即要求转体时梁体平稳、速度适中,最后能精确对中。因此,在转体前要进行不平衡重称重试验,以确定转体部分结构的最大静摩阻力矩、最大静摩擦因数、不平衡力矩、重心偏心量[2]。
在平转桥施工控制过程中,发现很多不平衡重称重试验报告和文献中试验得到的静摩擦因数与设计值相差较大,比试转时平转得到的静摩擦因数偏小[3-5]。静摩擦因数偏小将直接导致牵引力计算值小于实际牵引值,影响转体牵引施工控制的可靠性;还会影响转体惯性转动距离,造成精确对中困难。因此准确计算最大静摩擦因数非常重要,而最大静摩擦因数是根据不平衡重称重试验得到的实测球铰竖转摩阻力矩反算所得,即要求竖转摩阻力矩计算公式准确[6]。本文将对不同的摩阻力矩公式进行推导和分析,并通过对10多座平转桥不平衡重称重试验和竖转试验结果进行统计分析,验证公式的合理性。
1 球铰竖转摩阻力矩测试原理
不平衡重称重试验采用球铰竖向转动法,主要原理是利用球铰在静摩擦状态与动摩擦状态之间的极限状态时,受力状态会发生突变,同时球铰处位移也发生突变[6]。称重时,当顶升荷载较小时,球铰处于静止状态,摩阻力矩等于顶升力矩,球铰处的位移为微小转动变形和上转盘弹性变形之和,顶升荷载与位移近似成线性关系。当顶升荷载较大,接近球铰最大静摩阻力矩时,整个转动体处在静止和滑动状态之间,摩阻力矩不再增加。如果变成滑动时摩阻力矩还会变小,此时球铰处的位移为转动变形或者球铰发生较大晃动,顶升力与位移不在是线性关系。通过不平衡重称重试验记录绘制顶升荷载-位移曲线,判定极限状态荷载值,计算得到最大静摩阻力矩、不平衡力矩、重心偏心量[7]。
2 竖转摩阻力矩计算
2.1 基本假设
假设在平转桥不平衡重称重试验时,转体部分梁体和球铰在梁中心线所在的竖向平面内发生微小的竖向转动。转体部分荷载全部由球铰均布承担,不考虑偏心情况及其他可变作用。球铰竖向转动摩阻力矩为上球铰与下球铰之间的摩擦面上的每个微小面积的摩擦力对过球铰中心竖转法线的力矩之和[7-8]。
2.2 摩阻力矩常规公式
常规公式的竖转球铰摩阻力矩计算模型见图1。该计算模型将球铰分为许多微圆环,对每个微圆环上的摩擦力对球铰中心O的力矩求和,就得到了摩阻力矩公式。由图1可知:

其中:
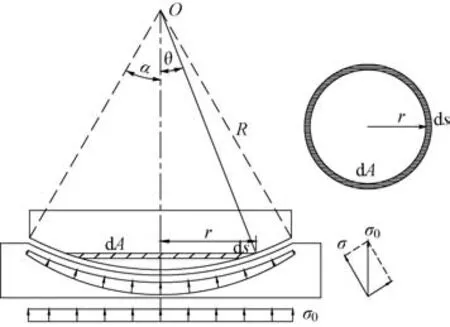
图1 常规公式摩阻力矩计算模型

式中:MZ为转动体竖转球铰摩阻力矩,kN·m;R为球铰的球半径,m;α为竖转平面球铰一半中心角,rad;N为转动体上部重量,kN;μ0球铰最大静摩擦因数。
2.3 新摩阻力矩公式
在摩阻力矩常规公式计算时,假设了每个微圆环上的摩擦力对球铰中心O的力臂为定值Rcosθ,进一步分析计算图示,可以发现这个假设是不准确的,Rcosθ为各微圆环到球铰中心的距离,而不是到竖向转动轴的距离。因此摩阻力矩计算公式存在较大偏差,推算得到的最大静摩擦因数也会与试转试验结果存在较大偏差,且偏小。

图2 新摩阻力矩计算模型
为了避免上述问题,建立新的球铰摩阻力矩计算模型见图2,假定不平衡重称重试验的竖向转动发生在zoy所在平面,整个梁体绕ox轴做微小转动,在垂直于ox轴的方向,将球铰摩擦面划分为微小圆弧,这些微小圆弧绕ox轴转动,而不是绕球铰球心O转动。微小圆弧中心线BC垂直于ox轴,且BC∥OZ(OA)。设∠AOB为θ,则圆弧的半径为rL=Rcosθ,圆弧上的球铰摩擦力到转轴的力臂相等,且为rL。
由图2可知:

β为圆弧一半中心角,β=α-θ。当θ=0时β=α;当θ=α时β=0。

由不平衡重称重试验可以得到转动体最大静摩阻力矩,按照式(7)可以反算得到最大静摩擦因数μ0。
2.4 摩阻力矩计算常数
根据上文,可以假定:MZ=Kμ0NR,K为球铰摩阻力矩计算常数,只与球铰设计参数有关。则

查阅国内2 家球铰生产厂家的产品手册,计算得到K值见表1和表2,由表可知:按照式(3)计算的K1一般在0.983~0.991,这与很多文献和资料上取值0.98或1.0 进行计算相符[1-8];按照式(7)计算的K2一般在0.640~0.644,K1/K2在1.53~1.55,两者相差比较大。

表1 球铰厂家1球铰摩阻力矩计算常数K

表2 球铰厂家2球铰摩阻力矩计算常数K
3 工程数据统计分析及验证
查阅平转桥不平衡重称重试验报告及文献[1-9],将球铰设计参数、转体自重和不平衡称重试验实测的摩阻力矩分别代入式(1)和式(2),反算得到竖转时的最大静摩擦因数。另根据试转时得到的启动牵引力,按照JTG/T F50—2011《公路桥涵施工技术规范》公式15.5.3反算可得平转时的最大静摩擦因数[10],数据统计结果见图3 和表3。由表3 可知:常规公式(3)计算得到的最大静摩擦因数与竖转时得到的最大静摩擦因数相比较,相差在-48%~-21%;新公式式(7)计算得到的最大静摩擦因数与竖转时得到的最大静摩擦因数相比较,相差在-21%~20%。新公式计算得到的最大静摩擦因数与试转时得到的最大静摩擦因数一致性更好,更合理。
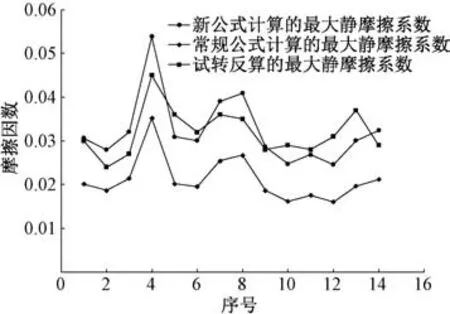
图3 摩阻系数比较

表3 平转桥不平衡重称重试验和试转试验结果摩擦因数统计
4 结语
平转桥在不平衡重称重试验时的新竖转球铰摩阻力矩假定计算模型与实际情况更相符,推导得到的摩阻力矩公式更准确。根据对10 多座转体桥不平衡重称重试验结果反算的最大静摩擦因数与竖转时启动力反算得到的最大静摩擦因数的比较分析,两者一致性更好,更合理,可以验证新公式的合理性和准确性。建议以后相关试验可以优先选用新公式进行计算,这样可以为平转桥牵引力计算,牵引设备、助推设备的选择,以及转体施工技术控制和安全评估提供更可靠、更准确的依据。

