系杆拱桥吊杆张拉方案优化试验研究
王莉
(中铁第一勘察设计研究院集团有限公司,陕西西安 710043)
系杆拱桥外部为静定结构,内部为高次超静定结构[1],吊杆内力的改变对全桥受力状态均有一定影响。系杆拱桥最常用的是柔性吊杆,其应力-应变曲线呈非线性,在长期荷载作用下会产生应力松弛和应力损失[2]。因此,系杆拱桥索力优化具有重要的实际意义。
朱敏等[3]通过零位移法和能量最小法的优化组合形成最优化的成桥状态,建立了施工期结构状态变量与成桥状态目标之间的关系,从而得到不同施工阶段合理的吊杆张拉力。任伟新等[4]指出将吊杆理想化为张紧的弦时,忽略了吊杆的垂度和抗弯刚度,在实际应用中会带来不可接受的误差。因此对弦公式进行了修正,采用能量法和曲线拟合法,建立了分别考虑索垂度和抗弯刚度影响、由基频计算索力的实用公式。张戎令等[5-6]从吊杆受力分析出发,结合抗弯刚度,在考虑转动惯量、剪切变形的影响和钢绞线及高密度聚乙烯(High Density Polyethylene,HDPE)2 种复合材料耦合振动的情况下,推导出吊杆铰接下索力计算公式。宋一凡等[7]引用斜拉索的动力计算长度概念得到吊杆的动力计算长度,然后将两端固结支承的拉索振动问题等效成两端铰结支承的拉索振动问题,从而解决了长期以来用振动法测估索力时遇到的有效吊杆长度取值难题。既有研究成果完善了索体系理论,为实际工程索结构张拉提供了借鉴。
本文以兰新二线新疆乌鲁木齐河特大桥为1 跨128 m 系杆拱桥为背景,建立室内1/16 缩尺模型,研究不同初张拉力时张拉过程中索力变化规律及拆除支架后系梁的应力和线形,可为同类桥梁的吊杆张拉方案提供借鉴和参考。
1 模型试验
1.1 模型设计
该桥为双线铁路桥,拱轴线为二次抛物线,矢跨比为1/5,系梁为单箱双室,每道拱肋上有17 组吊杆,每组2 根,采用先梁后拱的施工方法。对系杆拱桥进行缩尺模型吊杆索力试验,其几何缩尺比例为1/16,依据相似原理确定模型桥与原型桥面积、刚度、质量等参数的相似系数,并进行截面设计。系梁尺寸见图1,拱肋为哑铃形截面(拱肋壁厚82 mm,拱肋外经1.4 mm),模型桥吊杆采用6×19φ6.2 mm的钢丝绳,钢丝绳采用U形锁扣[5]将其锚固。
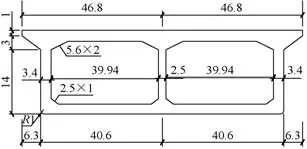
图1 系梁尺寸(单位:cm)
为控制各吊杆索力,在模型桥拱肋安装吊杆的位置安装S 形拉式传感器,在系梁底锚具上方安装压式传感器,通过连接DH3016 静态应变仪测试吊杆张拉过程中索力变化情况[8]。
吊杆上端与S 形传感器连接,吊杆下端穿过系梁并锚固于齿板上,最后取拉式传感器与压式传感器的平均值为该吊杆索力。在系梁L/8,L/4,3L/8,L/2,5L/8,3L/4,7L/8 截面布置百分表测试张拉过程中系梁挠度[9]。在系梁底缘拱脚和L/4,L/2,3L/4 截面布置应力应变计测试张拉过程中系梁应变。
模型桥测试试验见图2。

图2 模型桥测试试验
1.2 试验工况
为便于研究,将每道拱肋上的吊杆按小里程到大里程依次编号,每道拱肋上每组吊杆分为A,B 吊杆,见图3。
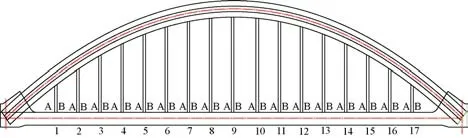
图3 吊杆编号
在系梁L/4,L/2,3L/4 跨底布置临时支墩,承担系梁、拱肋全部重量。张拉时,横向和纵向对称的4根吊杆同时张拉,根据吊杆数量和实际工程中千斤顶张拉吊杆情况,试验共分为10 个工况,每个工况共有8 根吊杆(工况3 除外)。如工况1,张拉吊杆号为5B13A,其左线和右线各有1 根吊杆,即2 根5B 和13A,共计4根吊杆同时张拉;然后张拉2 根5A 和13B;工况3 中,9A和9B为跨中吊杆,共有4根吊杆,一次张拉完毕。
系杆拱桥采用先梁后拱的形式,吊杆张拉方案的选取参考实际同跨径的3座桥梁张拉力进行吊杆张拉试验。依据相似比例将3 座桥的初始张拉力进行换算,对应的方案分别为方案1、方案3、方案4;将方案1对应桥梁的初始张拉力按加权平均值换算后作为方案2。
拟通过不同张拉力下吊杆内力重分布、系梁内力分布、成桥线形等进行分析。4 种张拉方案吊杆初始张拉力见表1。

表1 4种张拉方案吊杆初始张拉力 kN
2 试验结果分析
2.1 吊杆索力变化
4种张拉方案索力变化见图4。可知,系杆拱桥在分批张拉过程中,大多数吊杆表现出的规律是后批次张拉的吊杆索力对先批次张拉吊杆索力有明显的卸载作用。如首批张拉的5#,13#吊杆,自张拉开始,在其他吊杆分批次张拉过程中,该吊杆索力一直呈减小趋势,且张拉顺序越靠后吊杆受到的影响越小。在系梁拆除支架后发生了体系转换,由于系梁自重全部通过吊杆传递给钢管混凝土拱肋,因此各吊杆索力均有所增加。但在不同批次张拉过程中1#,3#,9#吊杆索力变化呈加载、卸载循环状态,表明少数吊杆在张拉过程中存在非线性应力重分布。
4 种方案下吊杆总张拉力分别为41.8,40.8,56.78,131.74 kN,方案1 和方案2 吊杆总张拉力相对较小,方案4吊杆总初张拉力最大,且其在不同工况吊杆张拉索力变化幅度较大。对比4 种方案下5#,1#,9#吊杆的索力变化情况,对于最先张拉的5#吊杆在方案1 中工况9 时索力减少为0,其余3 种张拉方案从张拉开始到张拉结束时索力分别减少了88.0%,78.9%和71.9%,方案3 和方案4 索力损失相对较少。1#吊杆为短吊杆,方案4吊杆初始张拉力最大,其值为3.45 kN,方案1 与方案2 吊杆张拉力相对较小,分别为1.37,1.20 kN。4 种张拉方案在体系转换前的张拉过程中索力变化较均匀,卸载也较小。对于中间9#吊杆,在张拉过程中吊杆处于加载、卸载的循环状态,从工况5到工况10 索力分别减少了63.7%,65.0%,58.6%和43.7%,方案3和方案4索力减少得相对较少。

图4 4种张拉方案索力变化
综合考虑吊杆初始张拉力、张拉过程中索力变化可知:方案4吊杆初始张拉力最大,张拉过程中吊杆索力相对较大且分布不均匀,该方案是不合理的;方案1与方案2中5#吊杆索力张拉完后卸载较大,也不合理;方案3比较合理。
2.2 恒载作用下系梁应力
恒载作用下系梁下缘应力见图5。可知,4种方案各控制截面最大应力为2.4 MPa,均满足规范要求。在跨中4 种方案截面下缘均受拉;在拱脚方案4 系梁下缘受拉,其余3 种方案系梁下缘受压。 方案1 和方案2各控制截面应力比较接近且系梁下缘拉压状况相同,方案3 和方案4 各控制截面应力绝对值小于方案1和方案2。说明方案3和方案4优于方案1和方案2。
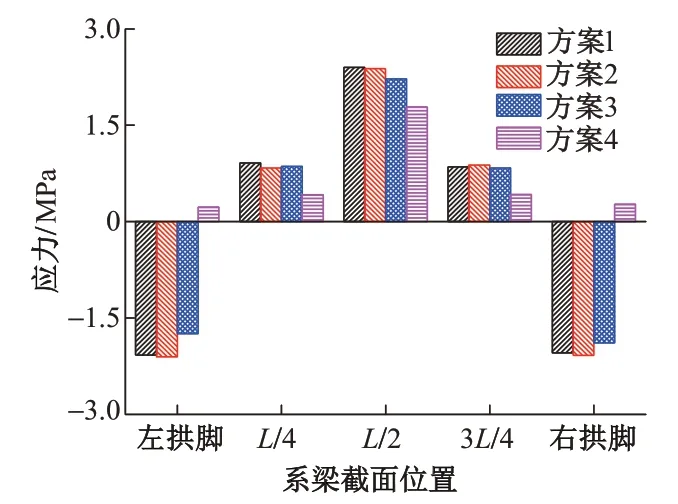
图5 恒载作用下系梁下缘应力
2.3 拆除支架后系梁线形
吊杆张拉后拆除支架后系梁变形见图6。可知,系梁变形整体上呈抛物线形,系梁挠度随吊杆初始张拉力增大而减小。在跨中系梁变形最大,方案1 中挠度最大值为2.93 mm,是方案2 的1.03 倍,是方案3 的1.2 倍,是方案 4 的 3.7 倍。方案 1 与方案 2 在跨中附近挠度差别较小,其他位置系梁变形基本相等。方案4 在L/8 和7L/8 处发生了上拱,而在跨中附近下挠,这不利于系梁浇筑时预拱度的设置。相比之下,方案3优于其他3种方案。

图6 吊杆张拉后拆除支架后系梁变形
3 结论
本文以1 跨128 m 特大桥为工程背景,按照实际结构的计算参数,在室内1/16 缩尺模型上进行了同一张拉顺序下不同吊杆索力试验,得出以下结论:
1)4 种张拉方案中,方案4 初始张拉力最大,吊杆索力卸载较大;方案1中先张拉吊杆索力被完全卸载,有一定的不合理性;方案1 与方案2 吊杆索力变化趋势基本一致;方案3 中各吊杆初始张拉力比原桥设计值偏大,但吊杆索力和系梁应力均满足规范要求。考虑吊杆受力及系梁应力和变形,方案3较为合理。
2)吊杆在张拉过程中表现出明显的应力重分布,后张拉的吊杆索力对先张拉的吊杆索力部分卸载,也会出现部分吊杆索力增大的现象,且应力重分布规律呈非线性变化。试验中最先张拉的5#,13#吊杆索力受到的影响最大。
3)拆除支架后系梁变形呈抛物线形,吊杆索力、系梁挠度和系梁应力均增大。

