拱桥短吊杆抗弯刚度的研究分析
古 锐,陈惟珍,徐 俊
(1.四川省公路规划勘察设计研究院有限公司,四川成都 610041;2.同济大学桥梁工程系,上海 200092)
宜宾南门大桥、新疆孔雀河大桥等中承式拱桥相继发生了桥面坍塌,该类事故具有很多相似之处,都是由于短吊杆骤断,导致桥面局部坍塌。惨痛的代价证明,大跨中承式拱桥的吊杆,尤其是短吊杆,受力非常复杂,既是桥梁的关键受力构件,也是桥梁的薄弱部位,常常成为控制此类桥梁寿命的关键构件,因此有必要对短吊杆的受力行为进行深入的研究[1]。
在拱桥分析计算中,常将吊杆作为轴向受拉杆件,一般不考虑其抗弯刚度,只考虑吊杆受拉的情况。但在实际桥梁运营中,吊杆的抗弯刚度是存在的,尤其是短吊杆,以现在广泛采用的成品吊杆拉索为例,由于钢丝有塑包带缠包扎紧,再外挤高密度聚乙烯护套,外径达 5~20 cm,钢丝之间还存在着互相摩擦、咬合等现象,所以吊杆拉索具有一定的抗弯刚度。
下文中拟以一座既有中承式钢管混凝土拱桥为背景,对短吊杆的抗弯刚度进行研究分析。
1 工程概况
某中承式大跨径钢管混凝土拱桥,主跨计算跨径为150 m,计算矢跨比为1/4.5。全桥横向设置2道拱肋,拱肋截面由4根φ660 mm钢管构成。桥面系采用吊横梁、纵置小T梁,吊杆纵向间距5 m,行车道梁为标准跨径5 m和7.5 m的钢筋混凝土T梁,桥面宽度为24.5 m。墩台基础均为明挖基础,引桥桥墩为柱式墩。全桥共有 46根吊杆,采用镦头锚锚固于拱肋上缘和横梁下缘;每根吊杆采用138根φS5平行钢丝束,采用外套φ110 mm×5 mm薄壁钢管并内填C10混凝土砂浆防护,桥梁立面布置及吊杆截面如图1所示。
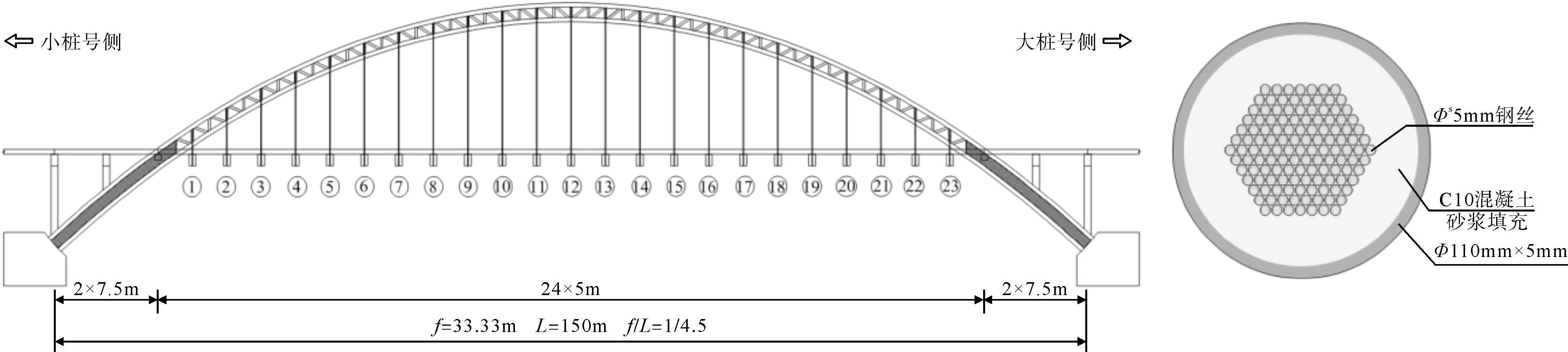
图1 桥型布置图及吊杆截面构造
采用有限元软件ANSYS建立桥梁的空间模型,如图2所示,全桥共计5 397个节点,5 868个单元。模型中吊杆采用空间单向受拉三维杆单元 Link10单元模拟,其余构件如拱肋、拱肋之间的腹杆、吊杆横梁、立柱横梁、立柱、横撑和桥面系主梁等均采用Beam188单元模拟。
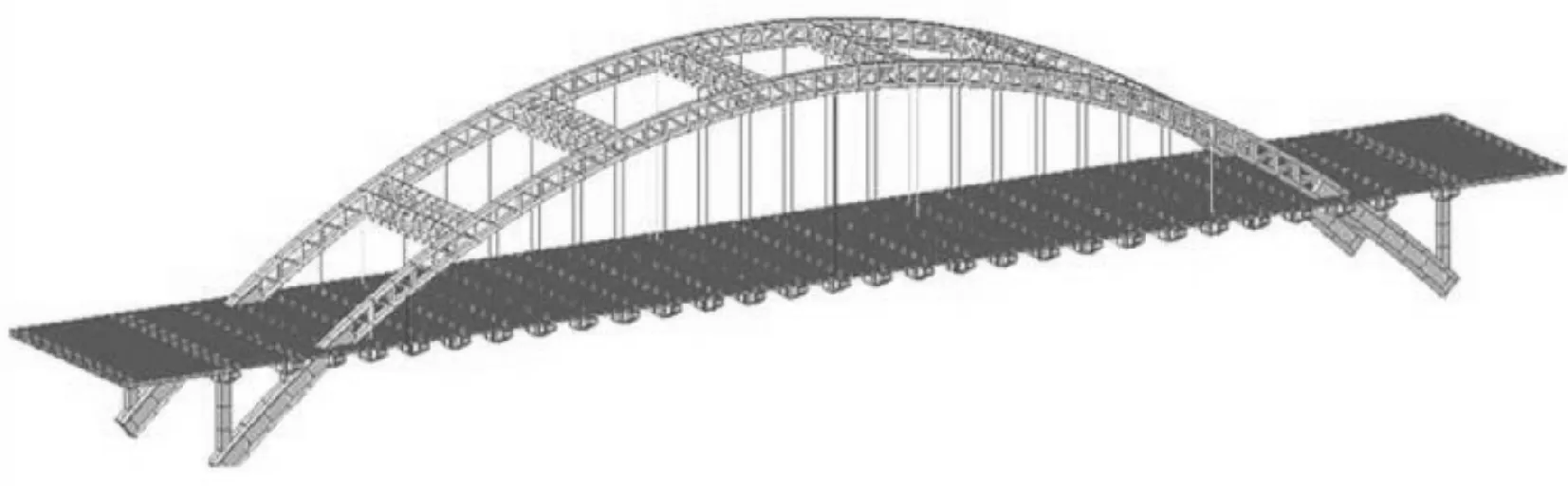
图2 拱桥空间有限元模型
2 吊杆抗弯刚度识别
该桥吊杆构造见图1,其高强钢丝面积为2 709.6 mm2,钢套管面积为1 649.3 mm2,内充砂浆面积为5 144.4 mm2,设计计算时只考虑了高强钢丝的轴向抗拉作用,其实高强钢丝仅占吊杆截面面积的28.5 %,而其余填充层的存在,必定将使吊杆刚度有所提高,同时具有一定的抗弯和抗剪能力。所以吊杆拉索也具有一定的抗弯刚度,但钢丝之间既不是松散的组合,也不是完全的整体,而是介于两者之间的状态,其抗弯刚度难以确定。所以在分析时,有必要考虑这两种极端的情况,即做两种假设:一种是最小刚度假设,即假设吊杆拉索由松散的钢丝构成,钢丝之间没有任何摩擦咬合,其刚度为单根钢丝抗弯刚度之和。另一种是最大刚度假设,即假设钢丝完全结合为一个整体,弯曲满足平截面假定,吊杆刚度近似地认为是与拉索截面积相同的圆形截面的抗弯刚度。显然,吊杆拉索的实际抗弯刚度介于这两种假设之间。
吊杆计入抗弯刚度的影响时,应用经典结构动力学原理,可解得两端固结的受拉吊杆频率方程为[2]:
αβ(1-cosαlcoshβl)+(β2-α2)sinαlsinhβl=0
(1)
式中,
ω=2πf
其中,m为单位长度吊杆的质量,l为吊杆计算长度,f为吊杆的频率,EI为吊杆的截面抗弯刚度。利用本方程计算吊杆拉力,只需直接将测得的某阶频率代入式中即可得出考虑抗弯刚度影响的吊杆拉力。
由于在实桥中吊杆拉力是惟一的,通过上式子,可知对应于不同频率阶数的实测吊杆拉力应该一致,据此即可识别出吊杆的实际抗弯刚度[3],具体识别过程如下:
(1)在合理范围内按一定步长遍取吊杆的抗弯刚度,例如,从0.1EI按0.05EI的步长取至0.9EI,其中I为按吊杆截面几何形状计算得到的截面惯性矩。
(2)对应于上述各个吊杆的抗弯刚度,将实测出的吊杆长度及各阶振动固有频率,代入式3.1中可以获取对应不同频率阶数的实测索力。
(3)由于吊杆拉力唯一,不同频率阶数的实测吊杆拉力应该一致,据此即可识别出吊杆的实际抗弯刚度。
该桥于2005年实施的荷载试验中,短吊杆频率识别精度较差,因此选取其中5号、12号吊杆,对其抗弯刚度进行了识别,图3、图4给出了吊杆在不同的抗弯刚度情况下根据各阶实测频率得到的实测拉力。
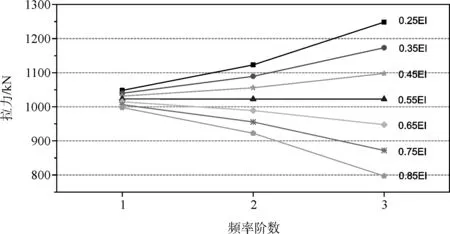
图3 实测5号吊杆拉力
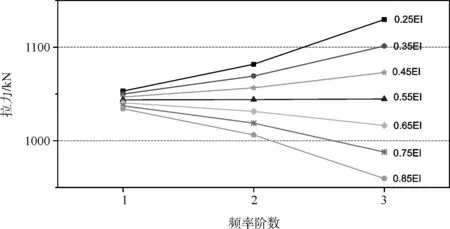
图4 实测12号吊杆拉力
从以上两图可以看出,当抗弯刚度取为0.55EI时,对应各阶实测频率的吊杆拉力连线几乎成为一根水平直线,即由各阶实测频率获得的实测拉力几乎相同,说明被识别吊杆的抗弯刚度应为0.55EI。事实上,吊杆的抗弯刚度属于吊杆的内在特性,在加工工艺、各截面参数相同的情况下,不随外因而改变。从本节选取的两根长短不同的吊杆来看,抗弯刚度识别均为0.55EI,这也说明了吊杆抗弯刚度的取值有相同的规律性。文献[3]利用某斜拉索不同时期的实测频率进行了多次索抗弯刚度的识别,结果也显示全桥斜拉索无论长短粗细,在各个时期其抗弯刚度识别结果均稳定。
以上识别结果,更长的12号吊杆,取不同的抗弯刚度其索力识别区间明显要小于5号吊杆的索力识别区间,这也表明吊杆抗弯刚度的取值对短吊杆张力影响较大。因此,下节计算中,拟考虑长度小于10 m短吊杆的抗弯刚度影响,抗弯刚度的取值为本节中抗弯刚度识别结果0.55EI。
3 恒活载对短吊杆截面应力的影响
对长度小于10 m的1、23号短吊杆,2、22号次短吊杆计入其抗弯刚度0.55EI,在已建立好的桥梁有限元模型中,将上下游侧共8根短、次短吊杆的只受拉Link10单元更换为考虑抗弯刚度的Beam188单元。
恒载作用下短吊杆内的应力主要包括轴向拉应力和弯曲正应力。图5、图6分别为恒载作用下上游侧1、2号吊杆应力比例和应力分布。由图可知,在恒载作用下,短吊杆内应力以轴向拉应力为主,弯曲正应力所占比例极低,基本可以忽略,这主要是因为,恒载作用主要是引起吊杆的轴向受拉变形,与吊杆的轴向受拉刚度有直接联系,并不受抗弯刚度的影响;从两图中也可以观察到,短吊杆由于抗弯刚度的影响,会导致吊杆内应力分布不均匀,但恒载作用下应力分布差别不大;短吊杆的弯曲变形主要是横桥向的弯曲变形,这与该桥采用的桥面体系是相符合的,通过吊杆下的横梁承担传递桥面荷载。

图5 恒载作用下的上游侧短吊杆应力比例

图6 恒载作用下的上游侧短吊杆应力分布(单位:MPa)
4 温度对短吊杆截面应力的影响
考虑结构整体温差的影响,结构整体温差按体系降温30 ℃计算,其位移计算结果与不考虑短吊杆抗弯刚度的结果相同,但是计入短吊杆抗弯刚度后,吊杆上下端由于桥面变形突出而产生纵向相对变形,从而在吊杆两端产生弯矩和剪力。由于拱肋和桥面纵向变位的最大差异在短吊杆区域,致使其端部产生较大的弯矩作用,内部钢丝受力复杂且不利,一部分处于外围的索体拉应力增大,另一部分索体拉应力则减小,尤其最短吊杆,弯曲、剪切变形程度最大,其受力情况最为不利(图7、图8)。

图7 整体降温30 ℃上游侧短吊杆应力比例

图8 整体降温30 ℃上游侧短吊杆应力分布(单位:MPa)
从图7、图8可知,相对于恒载作用,整体温度作用下,弯曲正应力效应明显,尤其是纵向的弯曲正应力。与不考虑短吊杆抗弯刚度结果相比较,降温30 ℃时1号短吊杆截面最大弯曲正应力达64.7 MPa,占恒载的17 %;2号次短吊杆的弯曲正应力占恒载比例分别为5.3 %。这也说明,随着吊杆长度的增加,抗弯刚度对吊杆受力影响的逐步减弱;但是若对短吊杆不考虑抗弯刚度的影响,整体温度作用下吊杆应力计算结果将是偏不安全的。
同时,从以上计算分析也可得知,整体温度作用下引起的短吊杆应力不均匀分布现象非常明显,降温30 ℃时1号短吊杆表层钢丝应力相差最大达到128 MPa。整体温差作用下,拱肋由于受拱座基础的约束,其纵向变形受到限制;而桥面两端由于简支在吊杆横梁上,其纵向变形几乎不受限制;这样,在相同的温差作用下,吊杆上下端由于桥面变形突出而产生纵向相对变形,从而在吊杆两端产生弯矩和剪力。尤其短吊杆区域,内部钢丝受力复杂且不利,一部分处于外围的钢丝拉应力增大,另一部分钢丝拉应力减小,但随到吊杆表面距离的增加,应力不均匀现象逐步减弱。
5 结论
通过吊杆的频率方程结合实测数据,识别了该中承式拱桥短吊杆的抗弯刚度,并经过分析比较得出:在恒载作用下,短吊杆由于抗弯刚度的影响,会导致吊杆内应力分布不均匀,但恒载作用下应力分布差异不明显;而由于抗弯刚度的影响,整体温度作用下会引起显著的短吊杆应力不均匀分布,导致外层钢丝应力相差达到了100 MPa以上,这是导致短吊杆内部应力不均匀的主要因素之一。
计算分析表明,中、下承大跨拱桥的短吊杆受力较为不利,是此类桥梁中的薄弱部位,应在设计中加强对短吊杆的关注。

