全视场外差白光干涉测量技术

汝洪武，吴玲玲，张文喜，李 杨*

全视场外差白光干涉测量技术

汝洪武1,2，吴玲玲1，张文喜2，李 杨2*

1西安工业大学光电工程学院，陕西 西安 710021；2中国科学院光电技术研究院计算光学室重点实验室，北京 100094

为了解决传统白光干涉测量技术中对线性位移机构的位移精度要求过高的问题，本文提出了一种全视场外差白光干涉测量技术。该技术主要通过使用存在差频的白光干涉信号作为光源来实现在大扫描步长和低扫描精度条件下相干峰位置的高精度检测。本文首先建立了白光外差干涉的数学模型，再根据数学模型提供的光强信号特性提出了整体系统设计方案，然后对测量方案的可行性进行了实验验证。最后针对多种误差对算法计算精度的影响进行了理论分析和数据对比。误差分析的结果表明：白光外差干涉测量技术提供更高的测量精度和更好的抗干扰性能，有效地降低了传统白光干涉测量对线性位移机构精度的严苛依赖，为光学自由曲面检测技术提供了更多的可选解决方案。

外差干涉测量；白光干涉测量；干涉测量算法

1 引 言

白光干涉测量技术是现阶段测量精度较高的一种测量技术，基于对白光自身的干涉特性和多种数据处理方法的研究表明，白光干涉测量能实现对实际距离的精准测量，并且已达到纳米级的测量精度以及毫米级的测量范围，因此得到了广泛的应用[1-2]。白光干涉测量精度与其使用的相干峰寻址算法的计算精度息息相关，希望通过算法能有效地提高测量精度、滤除测量噪声和提高测量效率等多种问题[3]。例如Baryshev等[4]希望通过希尔伯特变换算法实现白光干涉信号包络曲线的检测和噪声影响的分析，这是一种典型的通过算法减小噪声影响提高计算精度的方法。另外，高精度的白光干涉测量还依赖于高精度的线性位移机构和测量环境，为了规避这一严苛条件，近年来提出了很多优化方法。例如肖青等[5]提出了一种提高光学干涉系统稳定性的装置，通过提高干涉系统的抗干扰性从而提高干涉测量精度。张佳莹等[6]通过引入高速旋转的毛玻璃提高干涉信号的信噪比，进而提高干涉测量精度。国内外的学者大都从提高系统的稳定性和信噪比方面提高干涉测量精度，针对干涉原理上的创新较为少见。

为了扩大干涉测量的研究方向进而扩大在干涉测量中可使用技术的范围，提高干涉测量的多样性和可能性，日本学者Akiko和Hirokazu[7-8]提出了白光外差干涉测量技术，结合白光干涉测量和外差干涉测量实现了较高检测精度，使用相位探测器采集信号存在着成本高、适用范围窄、探测效率低以及核心算法较复杂等问题。随着声光移频技术的提高，具有更高稳定性和抗干扰性的外差干涉测量迅速发展[9-10]，本文研究了一种适用于高精度面形测量的全视场外差白光干涉测量技术，该技术将外差干涉测量技术与白光干涉测量技术相结合，通过连续的时域信号计算，降低干涉信号的随机误差。系统利用较大的纵向扫描步长与较低的扫描精度即可实现高精度的白光相干函数峰值检测，从而获得高精度的目标表面面形。

2 基本原理

2.1 白光外差干涉测量原理

白光干涉的本质是激光干涉的叠加，两路相同频率的激光重合时会产生长相干干涉现象，把这两束激光称为“激光对”。白光干涉是无数不同频率“激光对”的干涉相互叠加，由于干涉条纹宽度与激光的频率相关，因此不同频率“激光对”的干涉光强的波峰位置处处不同，随着光程差的逐渐增加干涉光强被均匀化，无数干涉光光强相互叠加时干涉光强对比度为零。只有在参考光与测试光光程差为零时，无数条激光干涉的波峰在同一处重合，因此白光干涉在零光程差处(零级条纹)光强最大，并随着光程差增大干涉信号的对比度逐渐降低。白光外差干涉测量是在白光干涉的基础上引入外差干涉的新的测量方式，外差干涉是两束不同的频率激光相互干涉，信号强度随时间变化，白光干涉测量具有白光干涉和外差干涉两种干涉的特性，本质上是无数个不同频率的外差干涉“激光对”相互叠加，光强信号受到时间和空间位置的共同影响。

2.1.1白光干涉信号

白光干涉信号的一般形式写为[11]

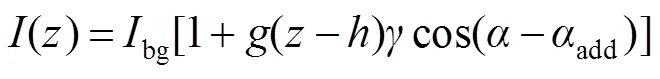
单色光外差干涉光强随着时间的变化光强呈正弦趋势变化，将外差信号引入到白光干涉信号后白光外差干涉信号受到光程差和时间的共同调制，相当于白光干涉信号在时域上又受到了时间的正弦调制，即：

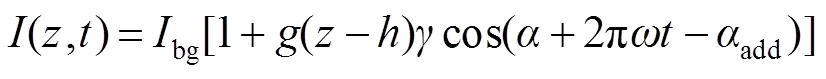
其中为两束信号的差频频率。光强变化示意图如图1所示。在某一特定空间位置的光强随着时间作正弦变化，在不同空间位置的振幅也在变化，因此传统白光干涉测量算法并不适用。

把光强投影到空间上如图1中黑色线段，虽然白光外差干涉信号在时间和空间上不断变化，但是在光程差发生改变时白光外差干涉信号的振幅在零光程差附近呈高斯分布，如图中红色曲线所示。再根据高斯曲线的特性探索白光外差干涉测量的算法。

2.1.2 相干峰寻址法

传统白光干涉测量大都采用相干峰寻址法，沿光传播方向移动标准面或者待测面来改变光程差，并在每移动一个步长后采集一个数据。白光外差干涉测量的采集方式与其类似，不同的是在每移动一个步长后采集一组时域上连续的数据，通过四步相移法求解出单个空间位置处的连续外差信号的振幅，按照原始扫描坐标排列，得到的光强振幅呈高斯分布，对该数据曲线高斯拟合，求得的极值点处的横坐标就是该点的对应高度。如图2(a)所示，扫描过程中振幅包络会在不同高度的点上各自出现一次相干峰峰值点，以峰值点的Z轴坐标为参照，两个峰值点的差值就是两采样点的高度差，如图2(b)所示。在待测面上选定一个基准点，求得待测面上的所有采集信号与基准点的高度差就可以计算出待测面型。

高斯曲线不同于白光干涉测量信号的曲线，在采样点相对较少时也能保证信号周期的完整性，同时具有较高的测量精度，大大降低了对高精度位移机构的依赖，提高了白光干涉测量技术的适用性，比直接对白光干涉的光强曲线拟合具有更高的拟合精度。

2.1.3 系统方案

全视场外差白光干涉测量可以通过图3所示的方案实现，白光光源被分光棱镜(BS)分光后经不同程度移频，再被平面镜和角锥棱镜反射后被BS合束，构成了两束中心频率有一定频差的白光光源，压电陶瓷(PZT)推动一路角锥线性移动完成扫描测量。为了实现较大口径的光学面型测量，干涉结构选取斐索干涉测量光路，如图所示，光源经由光纤自由发散出射，准直后被标准球面镜，可用于测量待测面，待测镜反射后被分光镜分为两路，分别到达探测器1和探测器2，探测器1用于监视调整，探测器2用于数据采集。

根据上述测量系统提出适用于白光外差干涉测量的处理算法，由于在测量过程中通过光源部分的调整就可以完成白光干涉测量的扫描，因此在测量球面面型时不受焦距偏离的影响，可以实现复杂曲面的测量。

2.2 白光外差干涉测量算法

白光外差干涉测量解算方法分为两个步骤，第一步：处理每一组的外差时域信号，获得该位置处的光强振幅信息，按空间位置对应排列后得到光强振幅信号曲线；第二步：对得到的光强振幅信号曲线高斯拟合，得到峰值处对应的横坐标，求解两点的高度差。

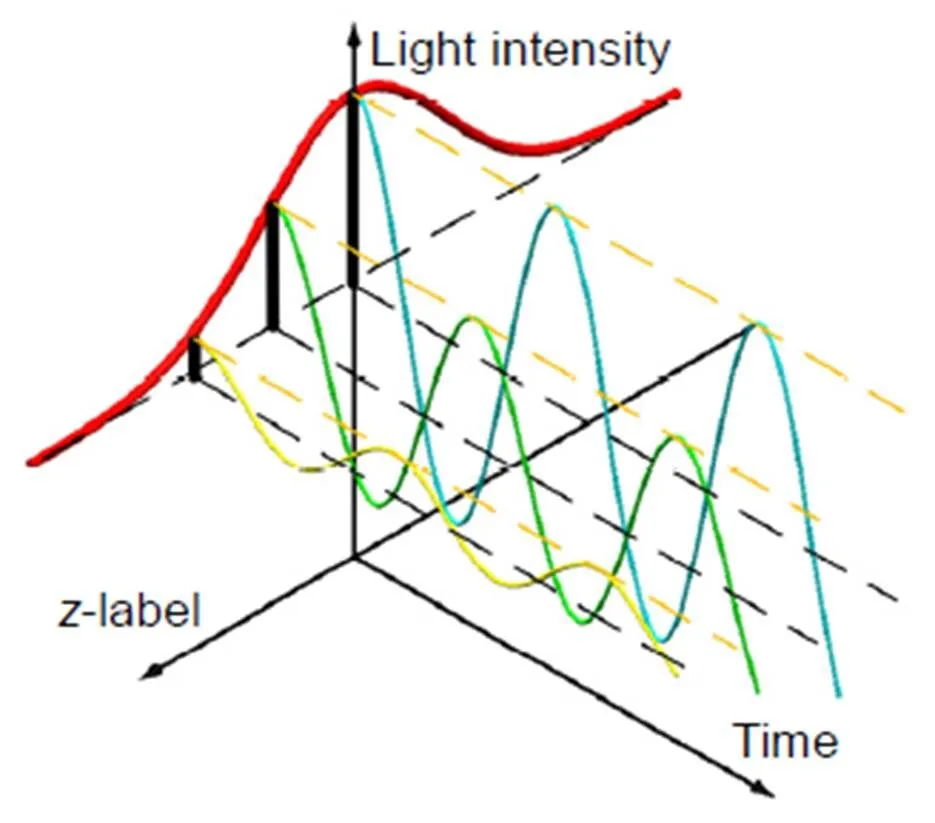
图1 白光外差干涉信号

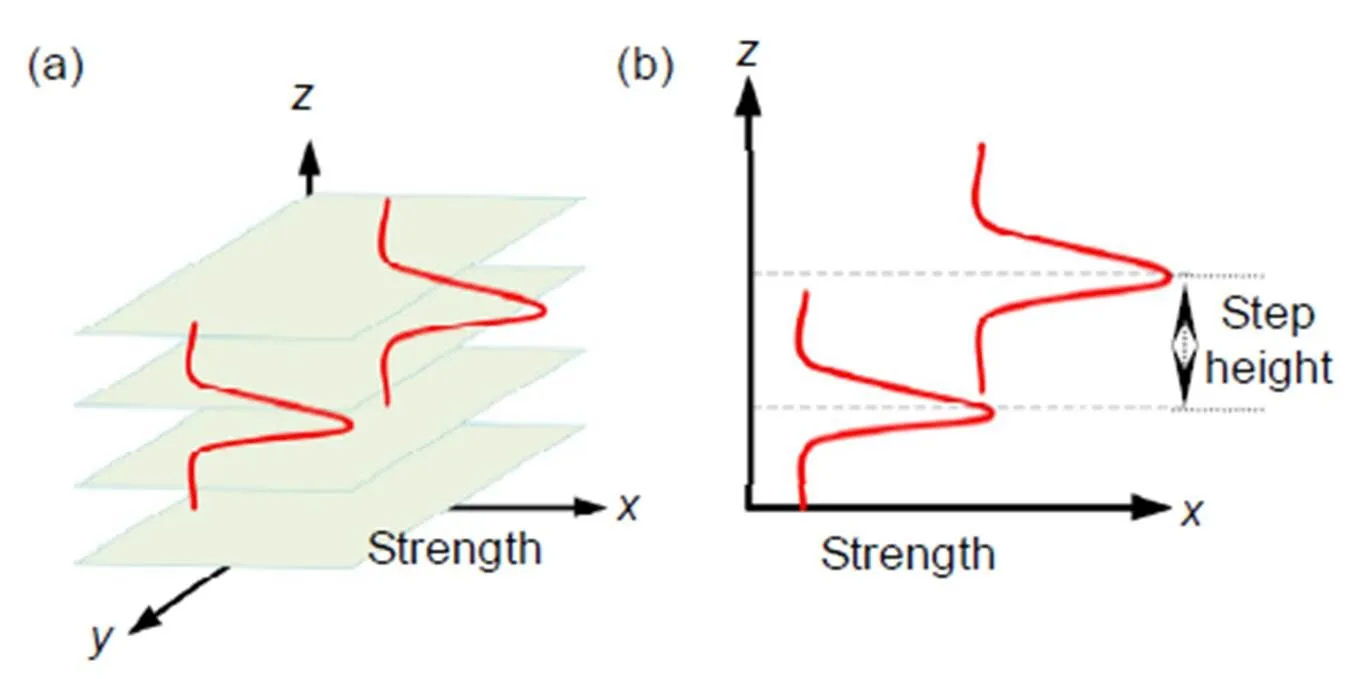
图2 相干峰寻址法示意图

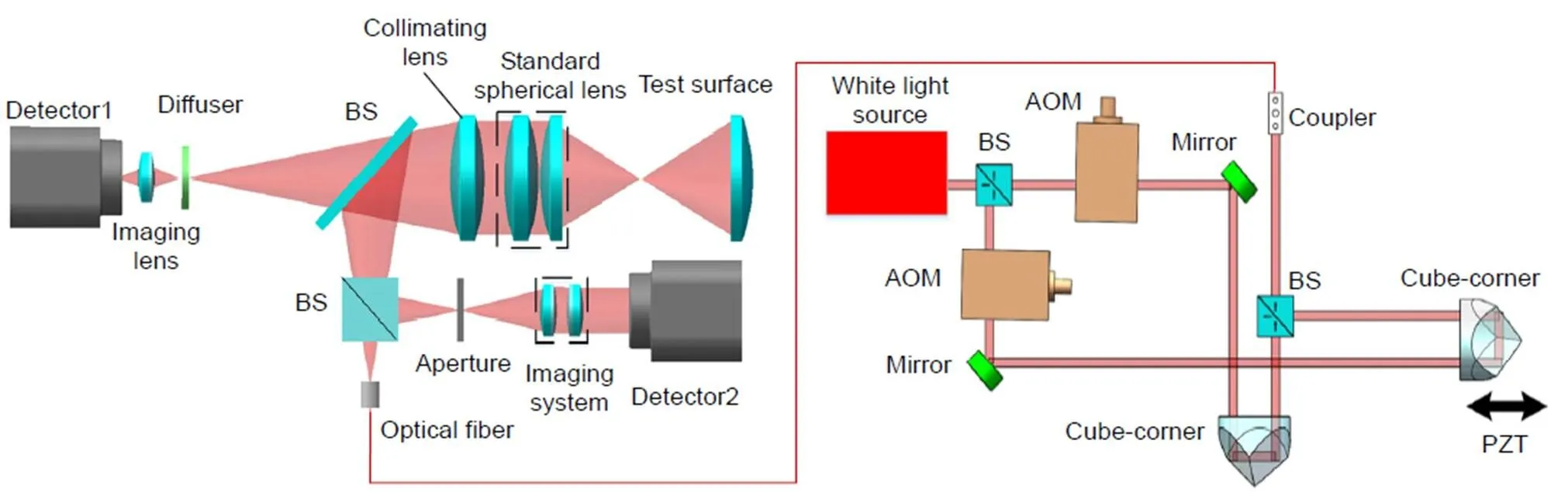
图3 白光外差干涉光路图

2.2.1 四步相移法求包络函数曲线

式(2)中当两束光平行时，令add=0，且当两参考面与待测面相对位置不变的情况下，只考虑时间因素引起的变化时：

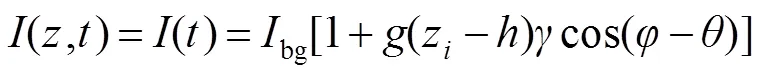
其中：为时间变化时引起的变化量，为空间相位和附加相位的引起的相位和。

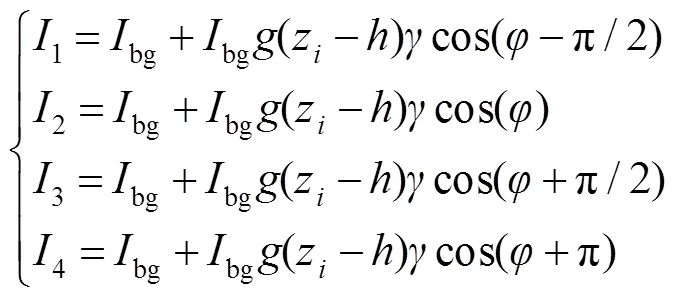
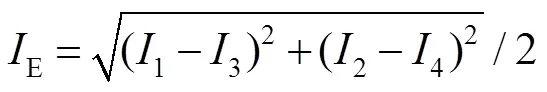
2.2.2 高斯拟合法求相干函数峰值坐标

高斯拟合法建立在非线性最小二乘拟合的基础上，已知白光外差干涉的光强包络符合高斯分布：

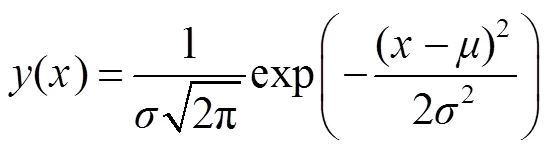
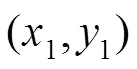
2.2.3 数据仿真结果

为了验证算法的可行性，使用Matlab仿真建立了一个22×20的矩阵台阶，台阶高度为5 μm。仿真光源中心波长为633 nm，相干长度为5 μm，双频光源的频率差为10 Hz。仿真探测器采样帧频为160 f/s，使用白光外差干涉测量算法对其处理过程如下，其中扫描总长度为15 μm，扫描步长为50 nm。在台阶不同高度两个面上的高斯包络曲线和拟合曲线如图4所示。

图5(a)为仿真台阶模型，高度为5 μm的22 pixels×20 pixels矩阵三维模型；图5(b)为通过该算法处理得到的复原台阶模型，验证了该算法具有很高的计算精度。完全理想的情况下白光外差干涉测量算法具有很高的计算精度，下面针对该算法的特性进行分析。

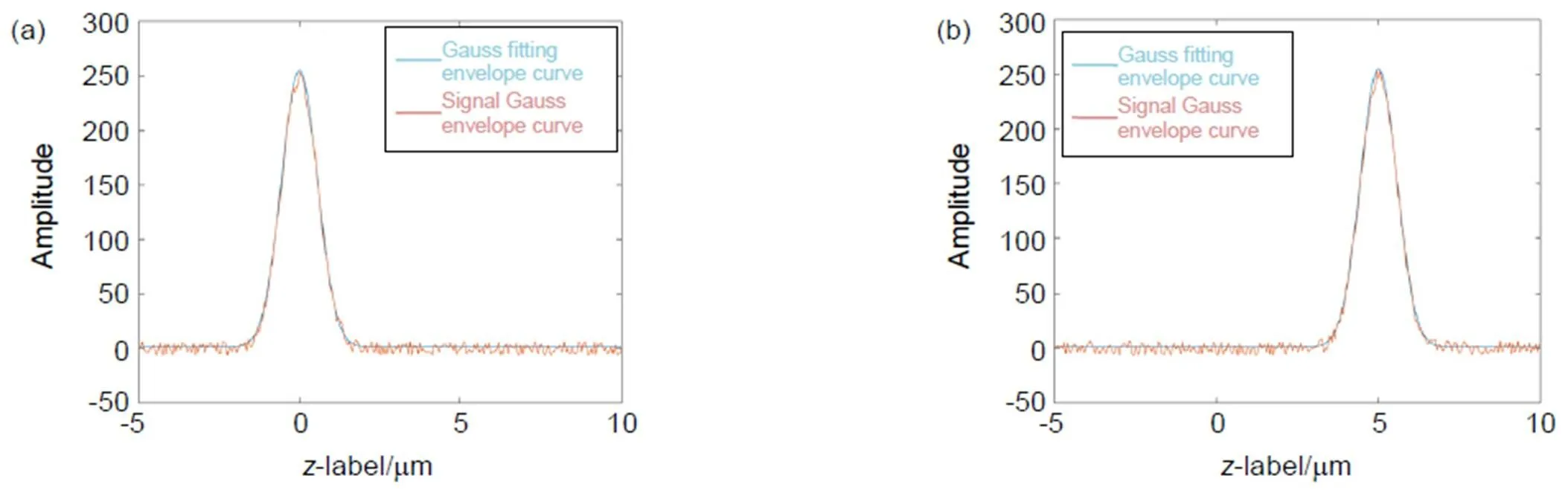
图4 实验数据拟合曲线。(a) 低位置处包络曲线；(b) 高位置处包络曲线

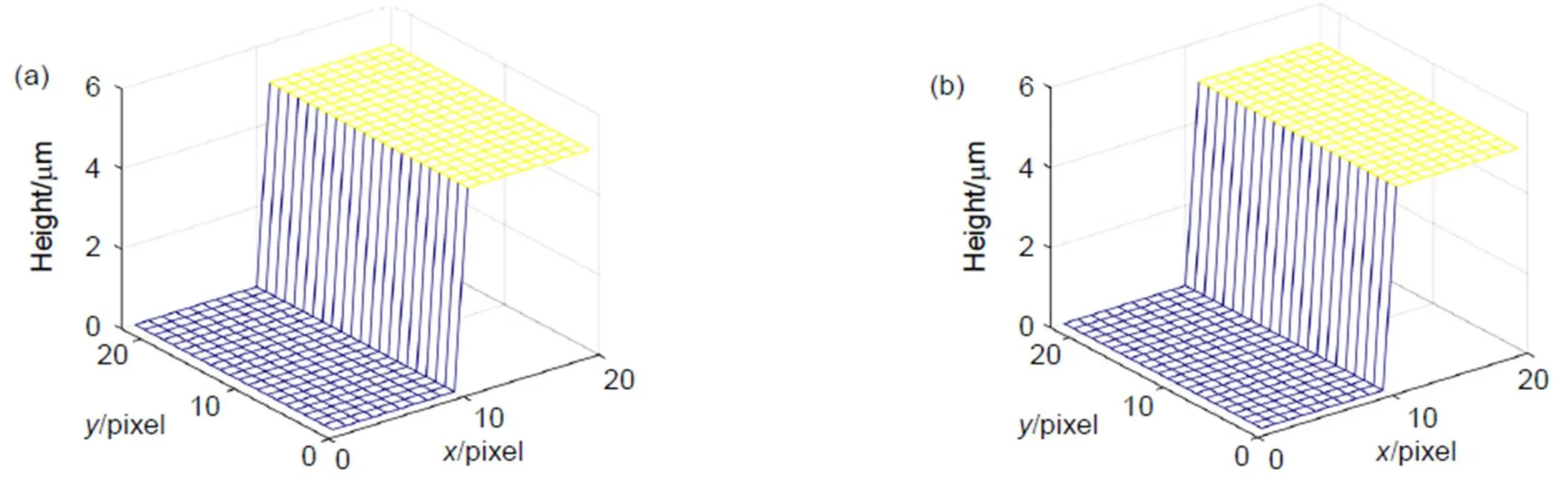
图5 白光外差干涉测量仿真结果。(a) 仿真台阶模型；(b) 复原台阶模型

3 分析与讨论

为了验证白光外差干涉测量更真实的测量效果，引入实际测量中可能出现的几种误差，另外选取白光干涉测量算法Fourier变换法[12-13]作为参考相比较。在一般测量过程中会获取待测面上所有点的完整的相干峰信号曲线，所以分析时仿真扫描长度大于相干长度，此时可以忽略扫描总长度引起的计算误差。在与上述台阶仿真的光源参数不变的情况下选取步长精度、扫描步长和探测器噪声三方面仿真比较。

3.1 扫描步长影响

白光干涉测量的精度很大程度上取决于扫描步长的大小，步长越小测量精度越高。根据光源的相干长度在5 μm左右，选择步长从10 nm到200 nm，另外，考虑到测量过程中仍会存在步长随机误差和探测器白噪声影响，为了更真实反映实际测量的计算精度，设定步长随机误差绝对值小于5 nm，探测器随机误差绝对值小于光强振幅的0.4%，对200次的仿真结果求平均，获得仿真结果如图6。

由于设定的步长误差是随机的，因此随着步长逐渐增大，计算误差的大小在稳定上升的同时有小范围的波动，可以得出白光外差干涉算法在步长达到200 nm时计算误差仍能保持在0.1 nm以下，高于传统白光干涉测量的Fourier变换法，且扫描步长增大时误差的上升速率也明显低于Fourier变换法，验证了白光外差干涉对扫描步长的影响具有较强的抑制能力。

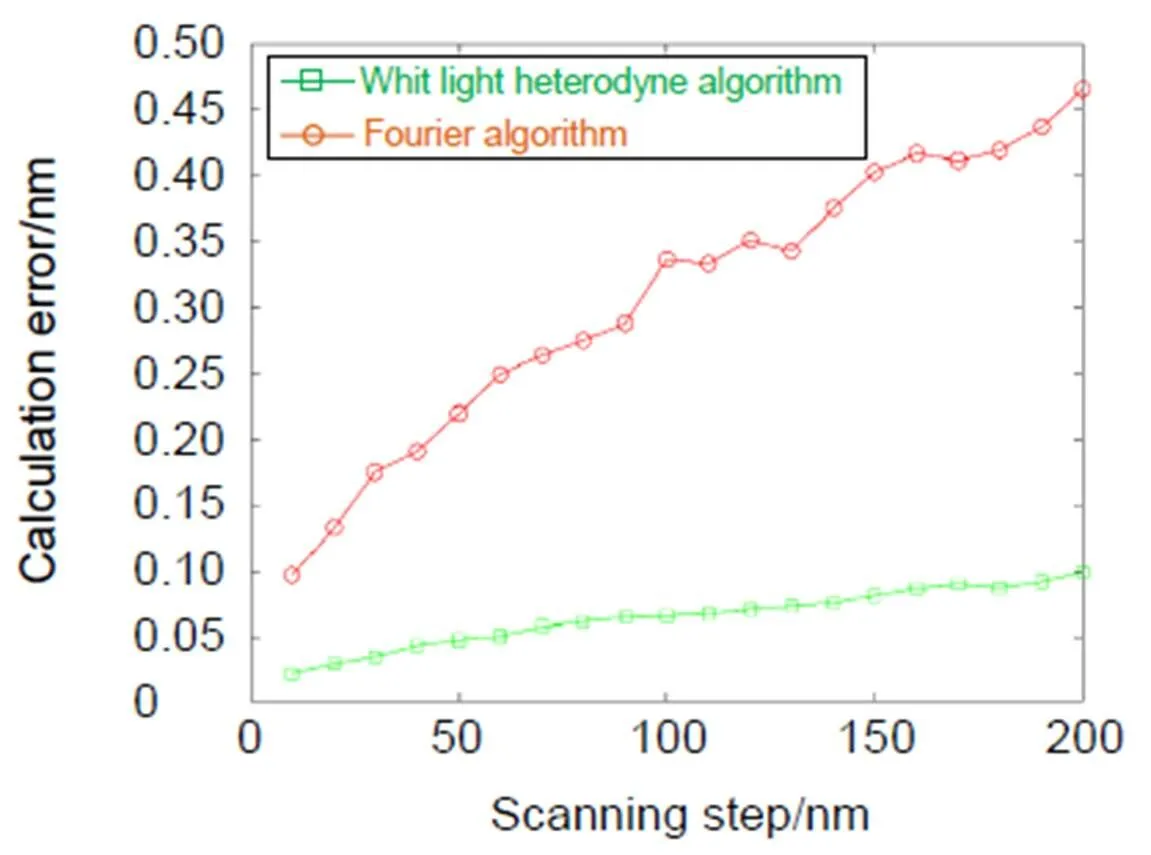
图6 步长大小对计算精度的影响

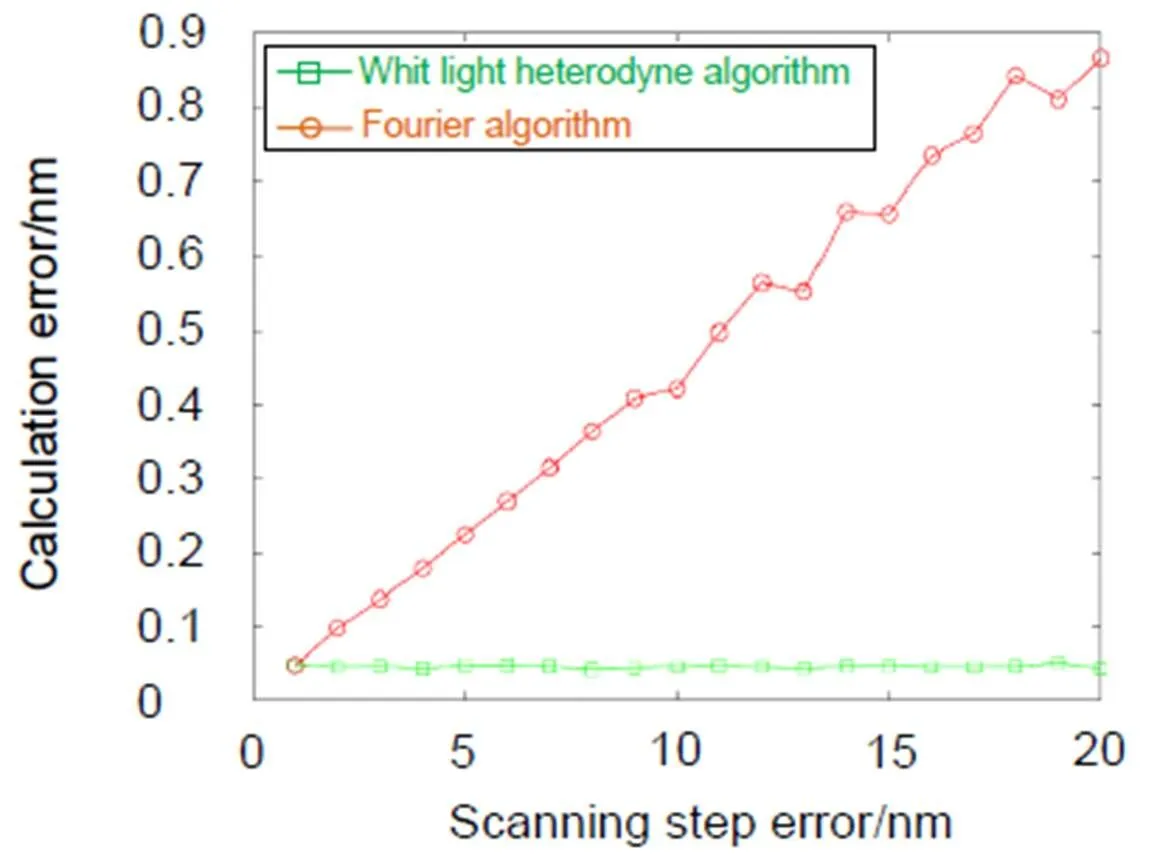
图7 步长精度误差对计算精度的影响

3.2 步长精度影响

另一个影响白光干涉测量精度的是扫描步长的误差大小。根据以上台阶仿真精度的扫描步长选择步长在50 nm，探测器随机误差绝对值小于光强振幅的0.4%，步长精度在步长的1 nm到20 nm时计算误差的仿真结果如图7所示。

由图7可得，白光外差干涉算法在1 nm到20 nm的扫描误差范围内具有较高测量精，几乎不受步长误差的影响，计算误差小于0.1 nm，完成了降低对高精度纵向扫描机构依赖的要求，而Fourier算法的计算误差随着步长误差的增大而迅速增大。验证了白光外差干涉对步长精度的影响也具有较强的抑制能力。

3.3 探测器噪声影响

考虑到实际测量情况，探测器具有一定的白噪声，影响测量数据的准确性[14]。选择扫描步长为50 nm，步长误差绝对值小于5 nm，探测器自身噪声占采集信号的振幅比从0.1%至2%变换时得到仿真结果如图8。

可见当探测器出现白噪声的时候，白光外差算法的计算精度随着探测器噪声的增大而增大，出现这种现象的原因是白噪声对四步相移法求光强包络时的影响较大，导致测得的光强高斯包络曲线误差变大，因此影响计算结果。从曲线图分析可知当探测器误差达到振幅的2%时，白光干涉测量算法的计算误差将超过Fourier计算方法，大于0.2 nm。所以选用此方法进行测量时要尽可能地挑选信噪比更好的探测器或提高干涉条纹的对比度。

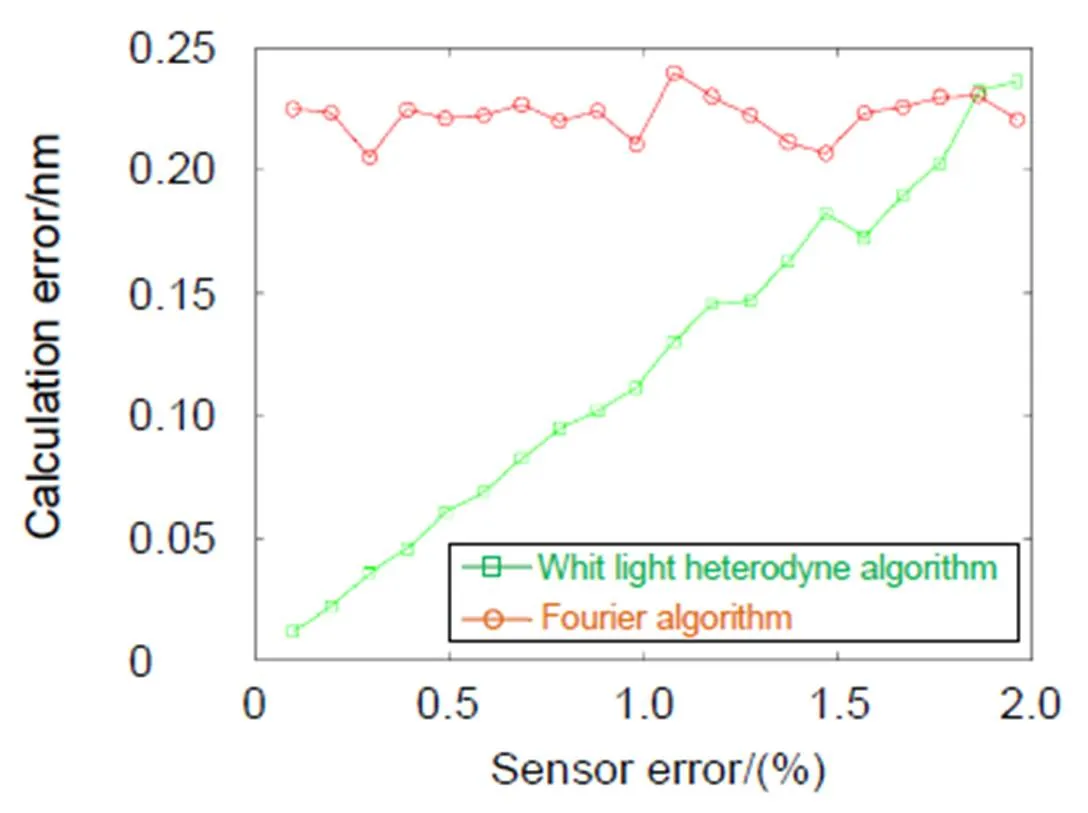
图8 探测器噪声对计算结果影响

在实际测量中需要根据测量精度要求合理选择光电器件，满足精度要求即可，在实际的实验测量中得到较好测量效果的同时也能有效地降低测量成本。

4 实验研究

根据现有实验设备搭建实验系统，实验光源相干长度190 μm，光源两束光频率差为10 Hz，相机采样频率为80 f/s，对球面光学元件测量搭建的实验系统如图9所示。为了进行初步原理验证，调整球面镜目标与参考波面产生相对较大角度倾斜。

实验测量过程中要求总扫描长度大于相干长度，为了保证每个采样点的干涉数据采集完整，光源内光程匹配移动角锥扫描步长为5 μm，共扫描54步，扫描长度为270 μm。图10为其中干涉图上某一点在两个不同扫描位置处获得的时域信号，在一个周期内选取相位间隔为p/2的四个数据点。图10(a)为光程匹配至相干峰峰值附近的时域光强信号，信号波动幅度较大；图10(b)为光程不完全匹配时的时域光强信号，信号波动幅度较小。信号的波动幅度可以反映该点的高度信息。

取目标上不同位置的两点，处理得到的相干函数高斯峰如图11所示，两点高斯峰峰值的不同反映了两个点的高度差。

初步实验结果表明了白光外差干涉测量技术具有目标面形高度探测的能力。由于实验设备的限制，无法进行更深入的实验验证算法的测量精度，为了探究该算法的计算精度和测量特性，仅采用仿真分析完成该算法的计算精度，根据仿真数据分析算法特性，进一步指导实验系统的优化改进。

图9 实验设备

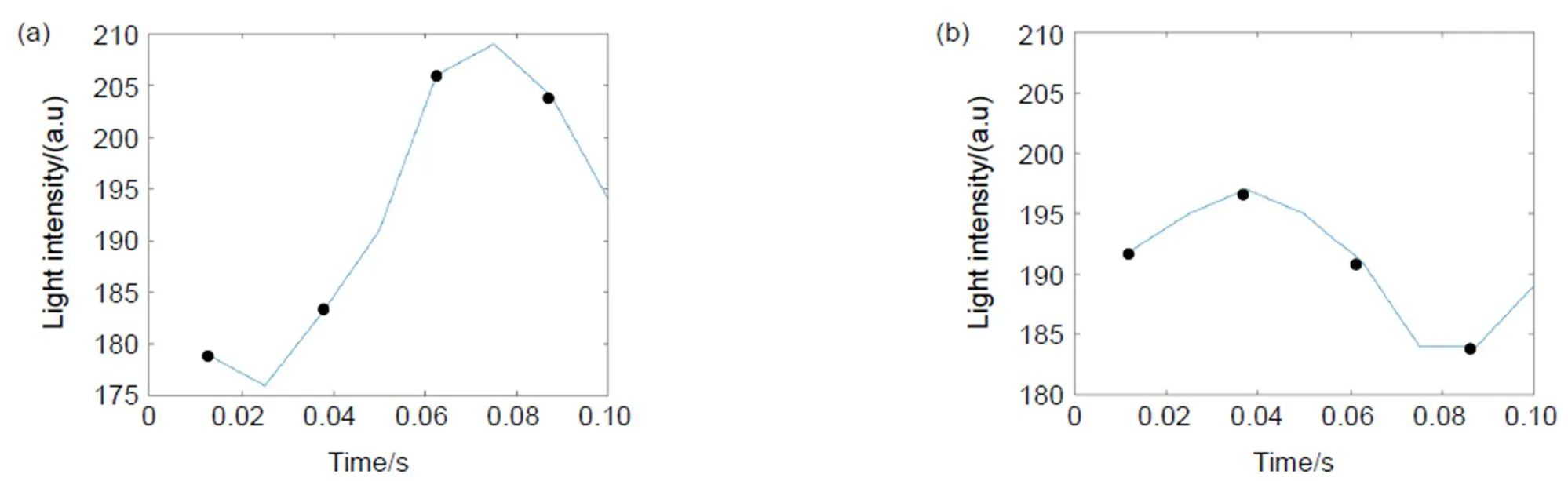
图10 时域光强信号。(a) 峰值处时域光强信号；(b) 普通位置处光强信号

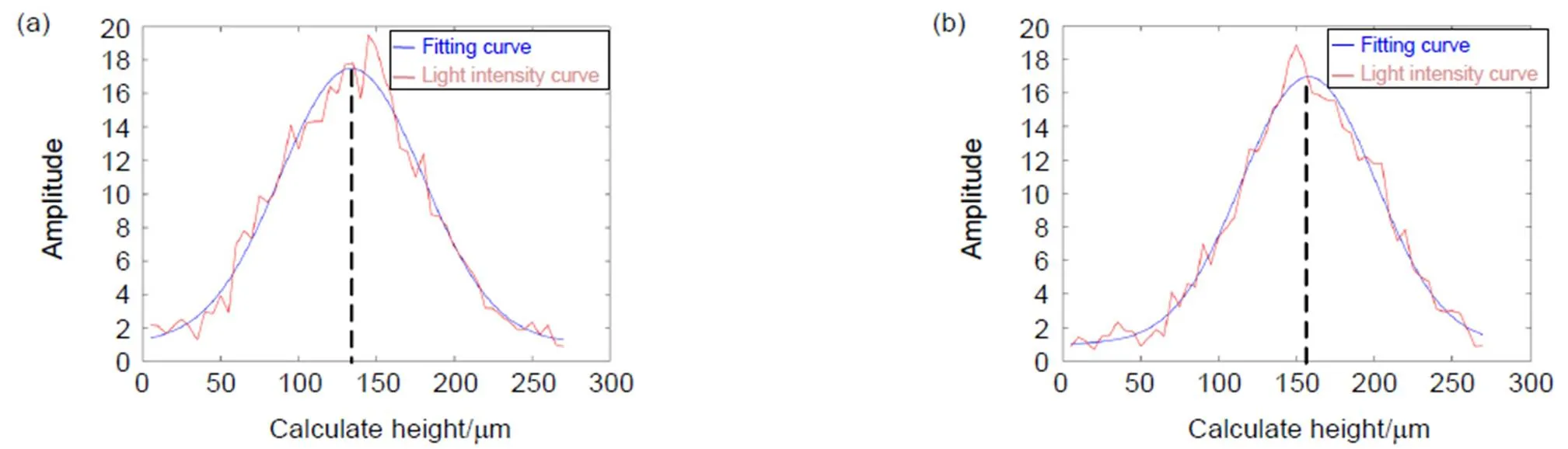
图11 实验数据拟合曲线。(a) 低位置处包络曲线；(b) 高位置处包络曲线

5 结 论

本文提出了一种全视场外差白光干涉测量技术以及一种可行的测量方案，用实验验证了方案的可行性，仿真分析了各种误差对实验结果的影响，结果表明：该技术能有效地降低白光干涉测量对高精度位移机构的依赖，提高白光干涉测量的稳定性。算法的仿真对白光外差干涉测量系统设计具有重要的指导意义和参考价值。

仿真结果分析验证了白光外差干涉测量算法相对传统白光干涉测量算法具有更高的计算精度，根据结果得出以下结论：

1) 全视场白光外差干涉测量算法在扫描步长范围从10 nm到200 nm内计算精度高于Fourier变换法，且随着扫描步长的增加计算误差上升趋势较为缓慢，在步长随机误差绝对值小于5 nm、探测器误差绝对值小于相干峰位置处光强振幅的0.4%、扫描步长为200 nm时计算误差仍小于0.1 nm，可以实现较大步长情况下的高精度测量。

2) 全视场白光外差干涉测量算法在扫描步长为50 nm、探测器误差绝对值小于相干峰位置处光强振幅的0.4%时、步长误差从1 nm到20 nm范围内计算精度高于Fourier变换法，且随着扫描步长的增加计算误差没有明显的波动，计算误差低于0.01 nm，对步长误差具有较强的抑制能力，在线性位移机构精度较差时仍能保持较高的计算精度。

3) 全视场白光外差干涉测量算法在扫描步长为50 nm、步长误差绝对值小于5 nm、低于相干峰位置处光强振幅2%的噪声等级范围内的计算精度高于Fourier变换法，计算误差小于0.1 nm。全视场白光外差干涉测量算法对探测器白噪声的抑制能力较弱，白噪声高于振幅的2%时计算精度低于Fourier变换法，应用该技术时应选取噪声小的探测器。

[1] Deng Q Y, Tang Y, Zhou Y,. High-resolution surface topography measurement based on frequency-domain analysis in white light interferometry[J]., 2018, 45(6): 0604001.

邓钦元, 唐燕, 周毅, 等. 基于白光干涉频域分析的高精度表面形貌测量[J]. 中国激光, 2018, 45(6): 0604001.

[2] Deng L J. White light interferometry measurement system and algorithm[D]. Hangzhou: China Institute of Metrology, 2015.

邓林涓. 白光干涉术的测量系统与处理算法的研究[D]. 杭州: 中国计量学院, 2015.

[3] Baryshev S V, Zinovev A V, Tripa C E,. White light interferometry for quantitative surface characterization in ion sputtering experiments[J]., 2012, 258(18): 6963–6968.

[4] Pavliček P, Michálek V. White-light interferometry—Envelope detection by Hilbert transform and influence of noise[J]., 2012, 50(8): 1063–1068.

[5] Xiao Q, Fu Q, Zhang D L,. A method to improve the stability of the optical interference system[J]., 2017, 44(11): 1089–1093.

肖青, 傅谦, 张大龙, 等. 一种提高光学干涉系统稳定性的装置[J]. 光电工程, 2017, 44(11): 1089–1093.

[6] Zhang J Y, Wang H J, Zhu X L,. Effect of speeds of rotated diffuser on image quality of interference fringes[J]. O, 2018, 45(1): 170492

张佳莹, 王红军, 朱学亮, 等. 毛玻璃转速对干涉条纹成像质量的影响[J]. 光电工程, 2018, 45(1): 170492.

[7] Hirai A, Matsumoto H. High-sensitivity surface-profile measurements by heterodyne white-light interferometer[J]., 2001, 40(3): 387–392.

[8] Matsumoto H, Hirai A. A white-light interferometer using a lamp source and heterodyne detection with acousto-optic modulators[J].1999, 170(4–6): 217–220.

[9] Gross M, Goy R, Forget B C,. Heterodyne detection of multiply scattered monochromatic light with a multipixel detector[J]., 2005, 30(11): 1357–1359.

[10] Wu Z, Zhang W X, Bin X L,. Full-field heterodyne dynamic interferometry based on Hertz-level low differential-frequency Acousto-Optic Frequency Shifter[J]., 2017, 10329: 1032905.

[11] Yang W P. The research of ultrasonic signals demodulation technology in the laser heterodyne interference[D]. Taiyuan: North University of China, 2016: 6–9.

杨玮萍. 激光外差干涉中超声信号的解调技术研究[D]. 太原: 中北大学, 2016: 6–9.

[12] Deck L, de Groot P. High-speed noncontact profiler based on scanning white-light interferometry[J]., 1994, 33(31): 7334–7338.

[13] Hart M, Vass D G, Begbie M L. Fast surface profiling by spectral analysis of white-light interferograms with Fourier transform spectroscopy[J]., 1998, 37(10): 1764–1769.

[14] Liu Z Y, Chen L, Zhu W H,. Oblique incidence dynamic phase-shifting interferometer based on inclination angle deflection[J]., 2019, 46(8): 180516.

刘致远, 陈磊, 朱文华, 等. 变倾角移相斜入射动态干涉仪[J]. 光电工程, 2019, 46(8): 180516.

Full-field heterodyne white light interferometry

Ru Hongwu1,2, Wu Lingling1, Zhang Wenxi2, Li Yang2*

1School of Optoelectronic Engineering, Xi'an Technological University, Xi'an, Shaanxi 710021, China;2Key Laboratory of Computational Optics, Acedemy of Opto-Electronics, Chinese Academy of Sciences, Beijing 100094, China

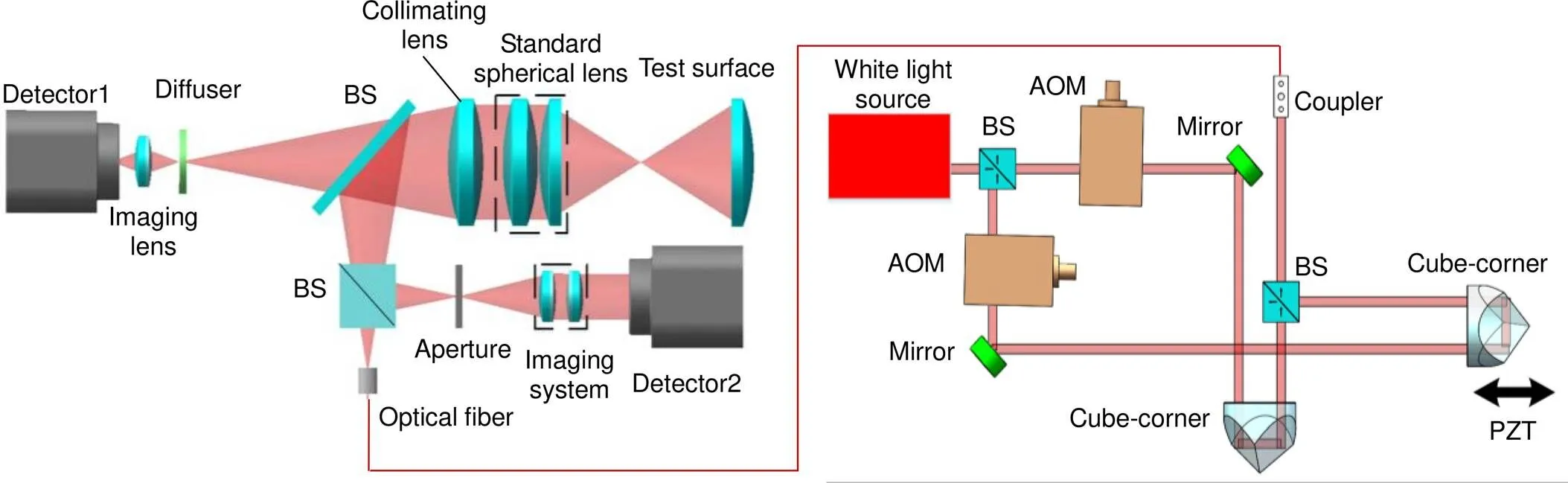
Schematic diagram of the white light heterodyne interference light source

Overview:In this paper, a measurement technique for full-field heterodyne white light interference is proposed. This technology uses white light interference signals with difference frequency to detect signal, aiming at reducing the high precision requirement of traditional white light interferometry for linear displacement mechanism. High-precision detection of coherent peak position under conditions of step size and low push-pull accuracy. Reducing the high precision requirements of the push-pull mechanism is of great significance for the development of white light interferometry. Firstly, the heterodyne signal is introduced on the basis of white light interferometry, and the mathematical model of white light heterodyne interference signal is established. According to the characteristics of light intensity signal and measurement target, a set of schemes for realizing white light heterodyne interference are proposed. The mathematical model of the difference interference signal has developed a special signal acquisition method, and the corresponding signal processing algorithm is proposed according to the signal acquisition method. The feasibility of the algorithm is verified by the simulation step measurement. Then the feasibility of the measurement scheme is verified by experiments. The experimental data analysis verifies that the system and algorithm principles are feasible. Finally, the effects of different scanning steps, scanning step precision and white noise of detector on the calculation accuracy of the algorithm are analyzed. The analysis results show that the full field white light heterodyne interferometry algorithm is more abundant than the traditional white light interferometry algorithm, and has higher measurement accuracy and stronger anti-interference. The step size is 50 nm and the step error is absolute. When the value is less than 5 nm, the calculation error in the case where the absolute value of the detector error is less than 1% of the amplitude can be stably maintained less than 0.1 nm, which can effectively reduce the dependence of the conventional white light interferometry on the high-precision linear displacement mechanism. Experiments have verified that this technique can achieve planar, spherical and aspherical surface measurements. This measurement technique can be used as an alternative to optical freeform measurement.

Citation: Ru H W, Wu L L, Zhang W X,Full-field heterodyne white light interferometry[J]., 2020, 47(2): 190617

Full-field heterodyne white light interferometry

Ru Hongwu1,2, Wu Lingling1, Zhang Wenxi2, Li Yang2*

1School of Optoelectronic Engineering, Xi'an Technological University, Xi'an, Shaanxi 710021, China;2Key Laboratory of Computational Optics, Acedemy of Opto-Electronics, Chinese Academy of Sciences, Beijing 100094, China

In order to solve the problem that the displacement accuracy of linear displacement mechanism is too high in traditional white light interferometry, this paper proposes a full-field heterodyne white light interferometry. The technology mainly uses the white light interference signal with difference frequency as the light source to realize the high-precision detection of the coherent peak position under the conditions of large push step and low push precision. In this paper, the mathematical model of white light heterodyne interference is established firstly, and then the overall system design scheme is proposed according to the light intensity signal characteristics provided by the mathematical model. Then the feasibility of the measurement scheme is verified by experiments. At the end, theoretical analysis and data comparison are carried out for the influence of various errors on the calculation accuracy of the algorithm. The results of error analysis show that the white-light heterodyne interferometry technology provides higher measurement accuracy and better anti-interference performance, effectively reducing the strict dependence of traditional white light interferometry on the accuracy of linear displacement mechanism, and is an optical free-form surface detection technology. More solutions are available.

heterodyne interference measurement; white light interferometry; measurement algorithm

Supported by National Natural Science Foundation of China (61605217)

P164

A

10.12086/oee.2020.190617

: Ru H W, Wu L L, Zhang W X,. Full-field heterodyne white light interferometry[J]., 2020,47(2): 190617

2019-10-15；

2020-01-09

国家自然科学基金资助项目(61605217)

汝洪武(1995-)，男，硕士研究生，主要从事白光干涉测量方面的研究。E-mail：ruhongwu_nic@163.com

李杨(1986-)，男，博士，硕士生导师，主要从事于计算光学干涉测量方向的研究。E-mail：liyang@aoe.ac.cn

汝洪武，吴玲玲，张文喜，等. 全视场外差白光干涉测量技术[J]. 光电工程，2020，47(2): 190617

* E-mail: liyang@aoe.ac.cn