两步式灵敏度矩阵法在卡塞格林望远镜装调中的应用

曹宇泽，马文礼

两步式灵敏度矩阵法在卡塞格林望远镜装调中的应用

曹宇泽1,2，马文礼1*

1中国科学院光电技术研究所，四川 成都 610209；2中国科学院大学，北京 100049

为了调节视场较大的卡塞格林望远镜的次镜位置，提出了两步式灵敏度矩阵模型的计算机辅助装调方法。在分析了传统的二次模型灵敏度矩阵法的缺陷的基础上，根据灵敏度矩阵的特点加入了精调步骤，对传统的灵敏度矩阵法进行了改进。针对卡塞格林系统，分析了各项泽尼克系数与失调量之间的关系，并对300 mm口径，0.6°视场的卡塞格林系统进行了校正仿真。仿真结果显示，传统的灵敏度矩阵法校正后沿、、轴偏移及绕、轴倾斜的失调量的均值分别为：-0.0684 mm、-0.0892 mm、0.0015 mm、0.0498°和-0.0444°，全视场波像差RMS均小于0.1(=632.8 nm)；两步式灵敏度矩阵法校正后的均值分别为-0.0018 mm、-0.0012 mm、0.0002 mm、0.0008°和-0.0012°，全视场RMS均小于0.03，明显优于传统的灵敏度矩阵法。

像差校正；灵敏度矩阵法；计算机辅助装调；卡塞格林系统

1 引 言

随着望远镜技术的发展，望远镜的口径和视场越来越大，光学系统的结构越来越复杂，加工制造和装调的难度也随之提升[1]。通过干涉仪等检测设备可以测量光学系统焦平面的光斑图，并通过光斑图计算得到各项泽尼克系数。为了得到良好的成像质量，采用计算机辅助装调技术，对光学系统进行实时检测并与理论结果进行比较，通过建立泽尼克系数与失调量之间的数学模型，精确地对元件的失调量进行校正[2-3]。应用最广泛的计算机辅助装调方法是灵敏度矩阵法。该方法是一种在分析像差特性的基础上，通过建立失调量与像差系数的数学模型来校正像差的方法[4-5]。最早的灵敏度矩阵是一阶模型[6-9]，校正后可达到全视场RMS为0.1的结果。中国科学院长春光机所的顾志远改进了灵敏度矩阵法，将数学模型扩展到二阶，并用改进的灵敏度矩阵法对500 mm口径的离轴望远镜进行校正，得到了全视场RMS均小于0.1的结果[10]。

本文分析了传统灵敏度矩阵法的缺陷，通过拟合的方法构建灵敏度矩阵并加入了精调的步骤，进一步提高校正精度。使用两步式灵敏度矩阵法对300 mm口径、0.6°视场的卡塞格林试验系统进行校正仿真，得到了良好的校正结果。

2 两步式灵敏度矩阵法原理

在光学系统中，元件的失调量会引入像差，单一元件有五个自由度的失调量，分别为沿轴偏移、沿轴偏移、沿轴(光轴)偏移、绕轴倾斜和绕轴倾斜，用D、D、D、T、T来表示，光学系统的像差可以用泽尼克多项式形式表示。根据泰勒定理，失调状态下光学系统泽尼克多项式系数可以表示为

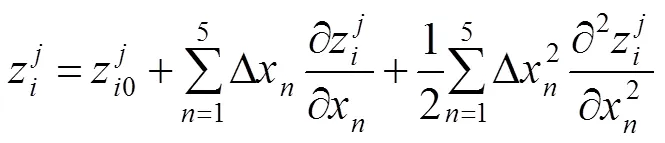
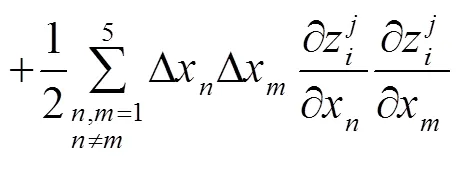
2.1 传统的灵敏度矩阵法

传统的灵敏度矩阵法使用的数学模型是失调量和像差之间二次相关，仅进行单次校正。通过构建二次修正模型，得到各自由度的失调量和每个泽尼克系数之间的灵敏度矩阵，进而对失调量进行校正。二次修正模型表达式为

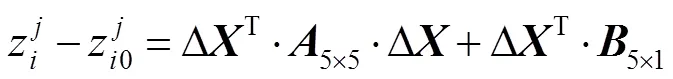
然而，由于不同自由度的失调量对泽尼克系数的影响并非完全相互独立，失调量不同的情况下灵敏度矩阵也会随之变化。因此，传统的灵敏度矩阵法具有较大的误差。用拟合方法构建灵敏度矩阵并将像差校正分为粗调和精调两个步骤可以有效减小灵敏度矩阵变化带来的误差。

2.2 两步式灵敏度矩阵法

由于灵敏度矩阵会随着失调量的变化而改变，而且失调量越小灵敏度矩阵越接近线性，因此两步式灵敏度矩阵法分为粗调和精调两个步骤，粗调的目的是减小失调量，精调使用线性模型进行精确校正。

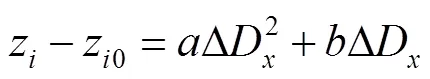
这种拟合得到的灵敏度函数精度较高，通过灵敏度函数可以构建对应位置的修正模型：

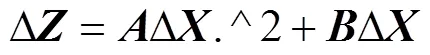
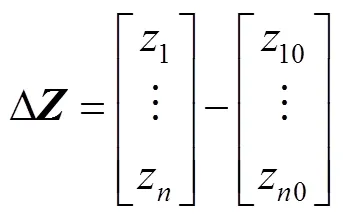
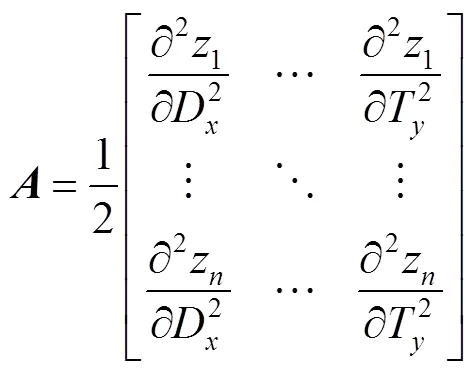
通过修正模型可以计算出粗调的校正量。

粗调后失调量显著减小，此时粗调中使用的灵敏度矩阵与粗调后对应位置的灵敏度矩阵有较大的偏差，如果重复使用粗调的灵敏度矩阵会导致校正结果偏差很大。由于各自由度失调量的绝对值小于0.1 mm或0.1°时失调量与泽尼克系数近似线性相关，因此精调采用失调量较小时的一阶灵敏度矩阵。修正模型的表达式为

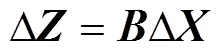
在构建灵敏度矩阵时，需要考虑所采用的泽尼克多项式系数。由于光学系统的失调量主要造成初级像差，对成像质量影响最大的是倾斜、离焦、彗差和像散，因此灵敏度矩阵的构建优先考虑0、1、2、…、8这几个系数。

在选择灵敏度矩阵的系数时，需要注意以下三点：

1) 选用的泽尼克系数必须能够反映所有自由度的失调量变化；

2) 泽尼克系数与失调量之间呈明显的线性或二次相关；

3) 泽尼克系数变化量不宜太小，能够确保灵敏度函数的精度。

因此，两步式灵敏度矩阵法与传统的灵敏度矩阵法相比，主要从泽尼克系数的选取、灵敏度函数的计算方法和校正次数这三方面进行优化，提高校正精度。

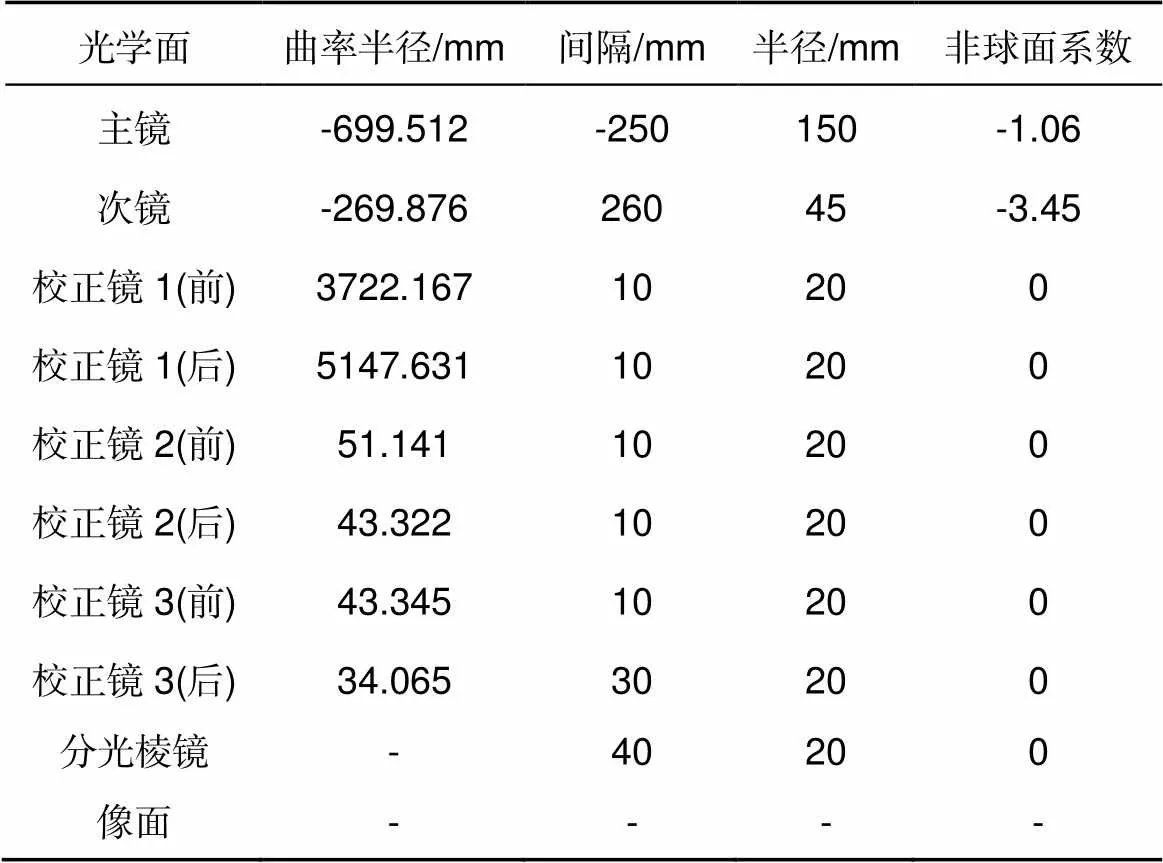
表1 卡塞格林望远镜光学系统参数

3 卡塞格林系统校正仿真

仿真使用300 mm口径、0.6°视场的卡塞格林系统，波段范围450 nm～800 nm，设计位置的全视场波像差RMS均小于0.03，并且要求50线对/mm处的MTF值大于0.6，具体参数如表1所示。

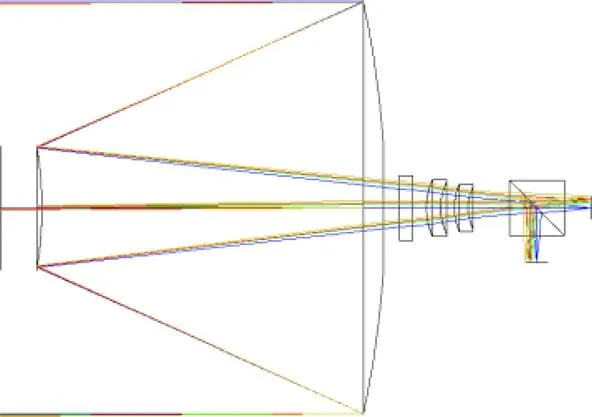
光学系统的结构图如图1所示。

校正过程中，以主镜为基准，逐一添加透镜并与设计位置对比，通过两步式灵敏度矩阵法可以精确地校正每一块透镜的位置。本文主要通过校正次镜位置来说明两步式灵敏度矩阵法的可行性，因此在后续仿真中将次镜以外的透镜置于设计位置，仅研究次镜的失调量校正。

以主镜为基准，保持其他光学元件位置不变，对次镜的5个自由度进行校正。首先需要选择灵敏度矩阵使用的泽尼克系数。在(0°，0°)、(0°，0.3°)、(0°，-0.3°)、(0.3°，0°)、(-0.3°，0°)这几个视场进行失调状态仿真并分析各自由度的失调量变化对泽尼克系数的影响。其中轴上视场各自由度失调量与泽尼克系数的关系曲线图如图2所示。

图中左列是受失调量影响较小的泽尼克系数曲线图，右列是受失调量影响较大的泽尼克系数曲线图，图中未出现的泽尼克系数代表不受对应自由度的影响。由曲线图可知，各自由度失调量对泽尼克系数的影响有三种：无影响、线性相关、二次相关，并且失调量对泽尼克系数的影响程度不同，其中D和T主要影响1和6，次要影响0、3、4和8；D和T主要影响2和7，次要影响0、3、4和8；D主要影响0和3，次要影响8。

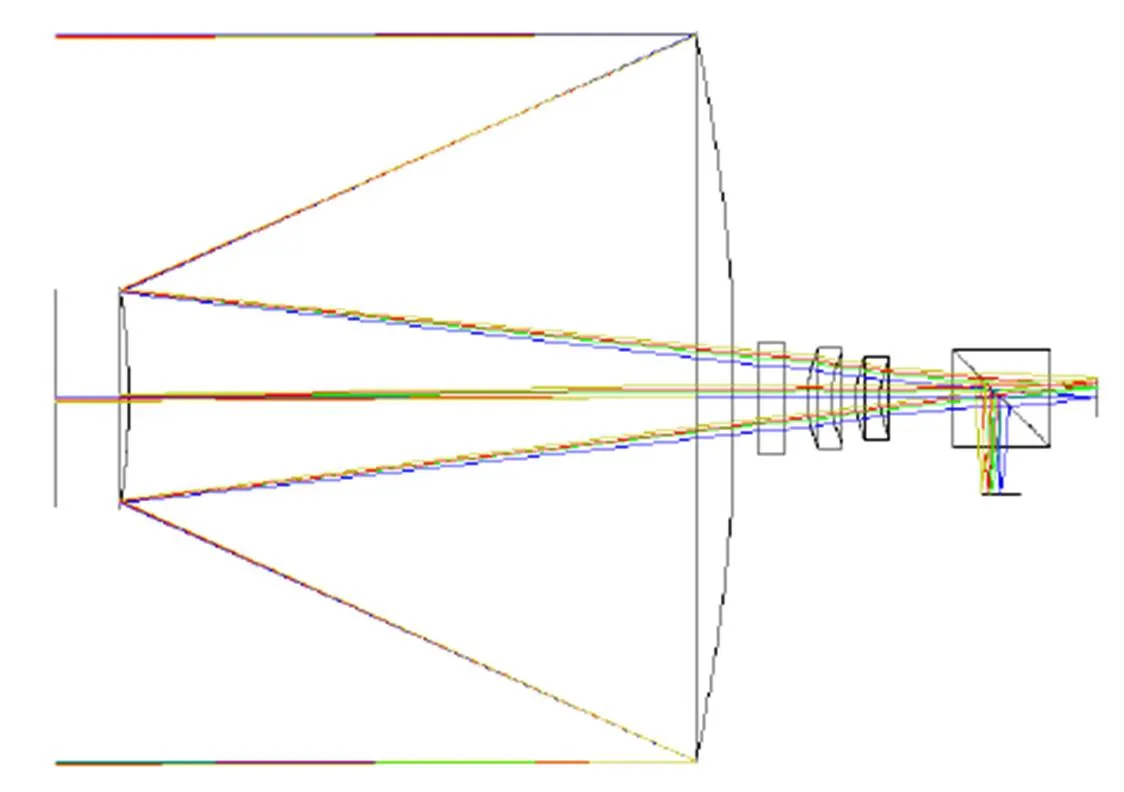
图1 卡塞格林系统的光学结构图

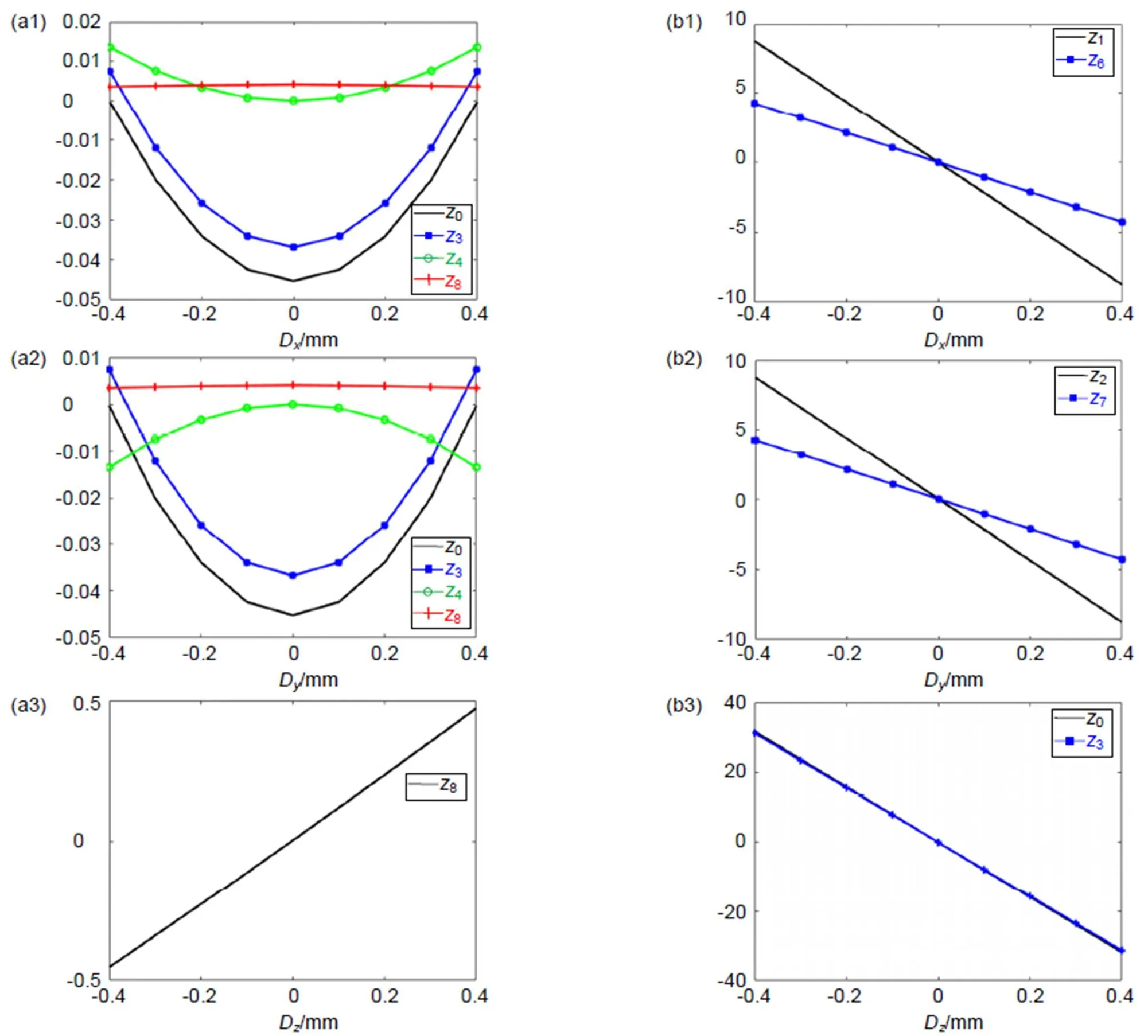
因此，根据泽尼克系数的选用原则，灵敏度矩阵的构建采用0、1、2、3、6和7这六项。

初始失调量随机选取，粗调后的失调量如表2。

为了说明不同失调状态的灵敏度矩阵的差异，第三组初始状态的轴上视场的灵敏度矩阵如表3所示(分号前后分别为二次系数和一次系数)：

粗调后的五个自由度失调量的均值分别为-0.0626 mm、-0.0594 mm、0.0005 mm、0.0513°和-0.0424°。由图2可以看出，只有受失调量影响较小的泽尼克系数才会与对应失调量二次相关。对于单一自由度，当失调量小于0.1 mm或0.1°时，二次函数和一次函数的偏差对失调量的影响小于0.0001 mm，因此失调量小于0.1 mm或0.1°时失调量与泽尼克系数近似线性相关，精调的灵敏度矩阵采用失调量为-0.0626 mm、-0.0594 mm、0.0005 mm、0.0513°和-0.0424°时的一阶灵敏度矩阵。精调后的失调量如表4所示。

粗调后第三组的轴上视场的灵敏度矩阵如表5所示。

由于粗调后光学系统已经较为接近设计位置，此时灵敏度函数用Matlab拟合为一阶函数时的误差已经小于二阶函数的误差。

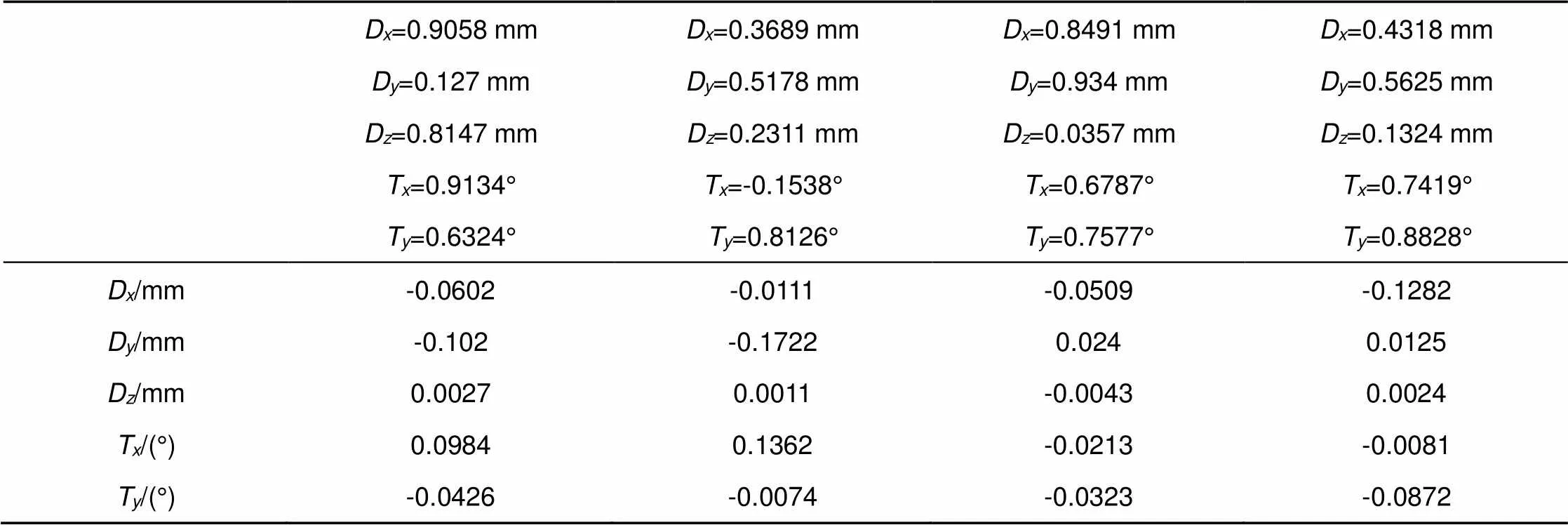
表2 粗调后的各自由度失调量

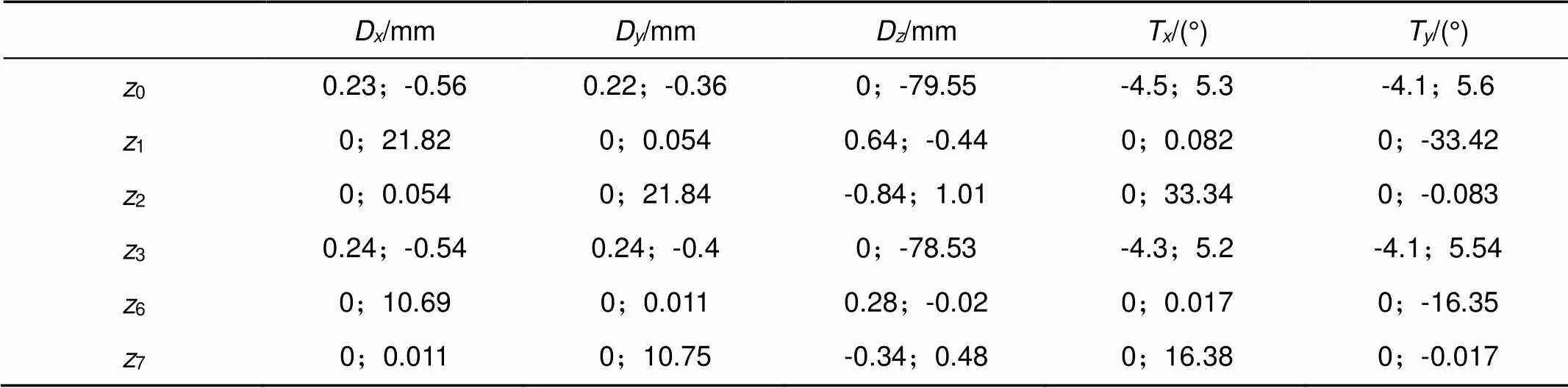
表3 初始状态的灵敏度矩阵

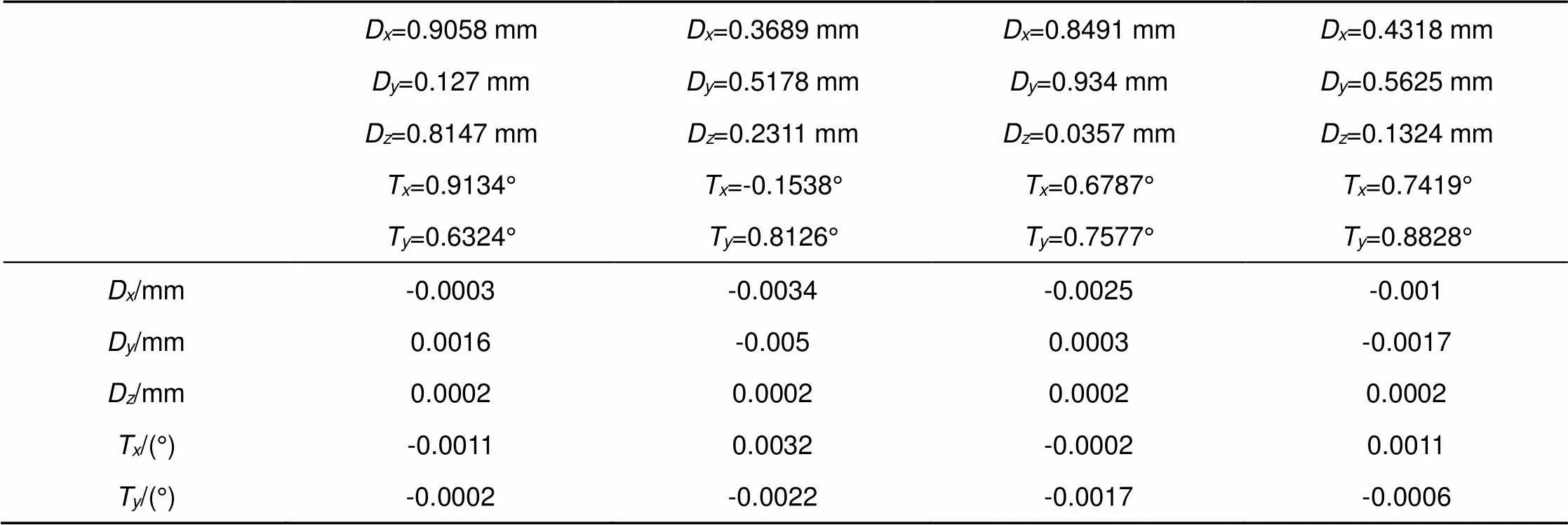
表4 精调后的各自由度失调量

第三组精调采用的一阶灵敏度矩阵如表6所示。

通过几个灵敏度矩阵可以看出，粗调后的灵敏度矩阵与初始位置相比确实有了很大的变化。传统的灵敏度矩阵法为单次校正，等同于默认灵敏度矩阵处处相等。因此，两步式灵敏度矩阵法确实比传统的灵敏度矩阵法精度更高。同时，采用精调矩阵也比重复使用粗调的二阶矩阵精度更高。

传统的灵敏度矩阵法校正结果如表7所示。

同时附上四组初始失调状态校正前后的泽尼克系数表，如表8所示。

4 结 论

本文在分析灵敏度矩阵的特点以及失调量对泽尼克系数影响的基础上，从更换选用的泽尼克系数、用拟合的方法构建灵敏度矩阵和增添精调步骤这三个方面对传统的灵敏度矩阵法进行了改进。对300 mm口径、0.6°视场的卡塞格林望远镜进行了多次校正仿真。仿真结果显示，传统的灵敏度矩阵法校正后沿、、轴偏移及绕、轴倾斜的失调量的均值分别为：-0.0684 mm、-0.0892 mm、0.0015 mm、0.0498°和-0.0444°，全视场波像差RMS均小于0.1；两步式灵敏度矩阵法校正后的均值分别为-0.0018 mm、-0.0012 mm、0.0002 mm、0.0008°和-0.0012°，全视场RMS均小于0.03，校正后的光学系统接近设计位置，明显优于传统的灵敏度矩阵法，说明了两步式灵敏度矩阵法对卡塞格林望远镜的装调具有很好的实用价值。

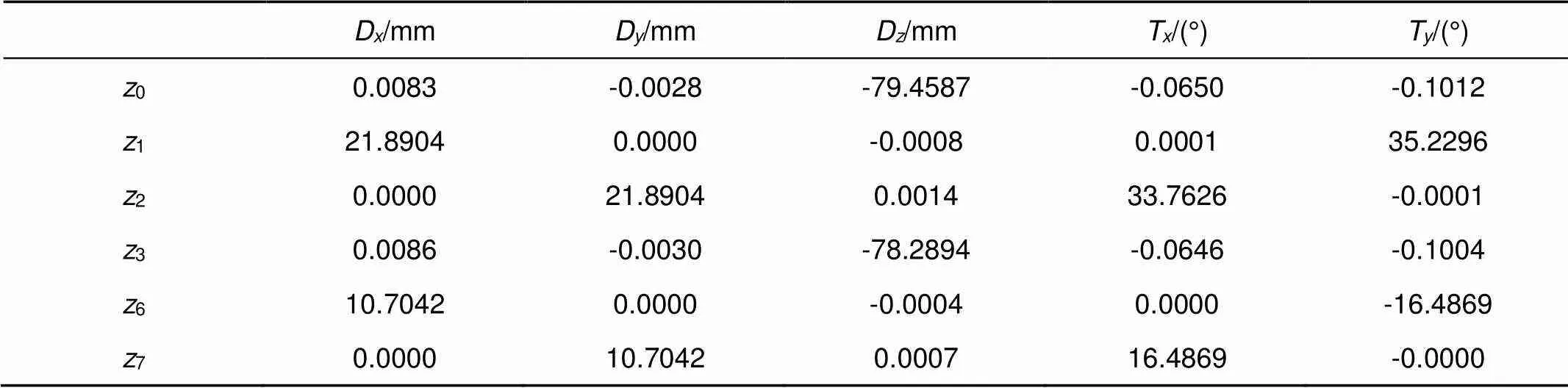
表5 粗调后的灵敏度矩阵

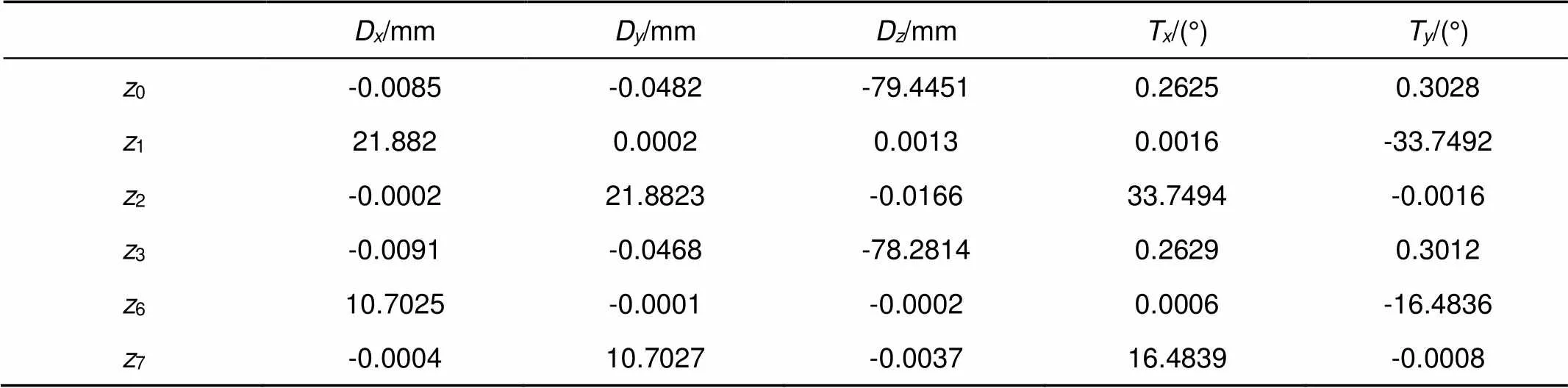
表6 精调采用的一阶灵敏度矩阵

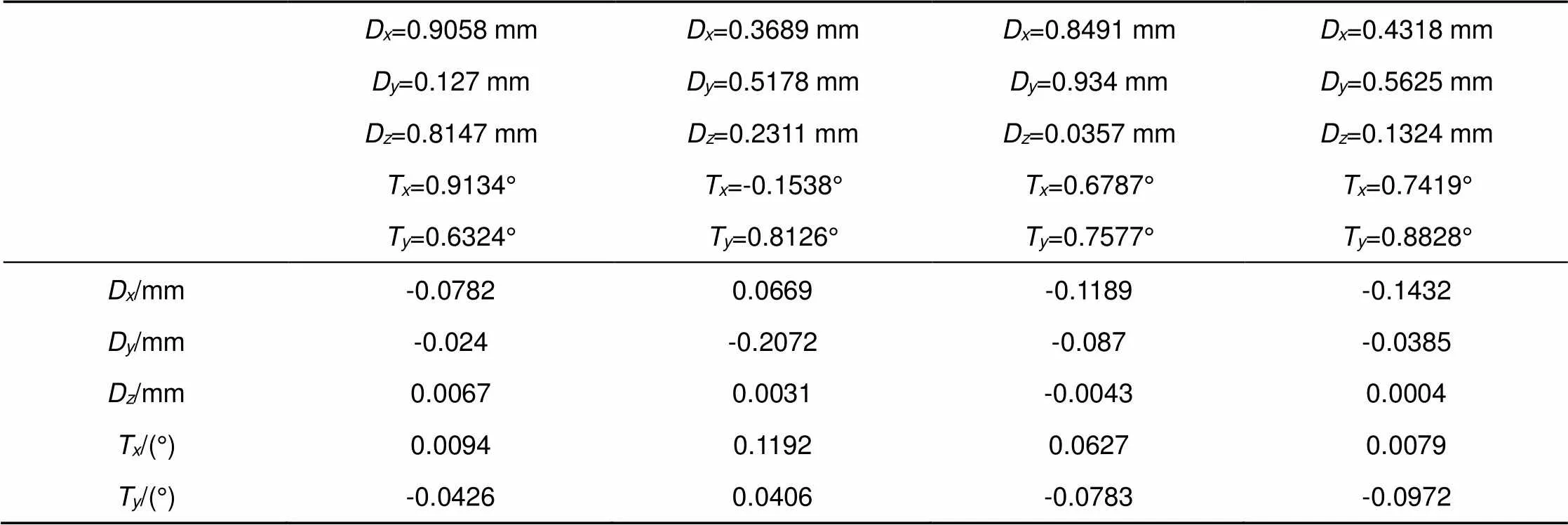
表7 传统的灵敏度矩阵法校正后的失调量

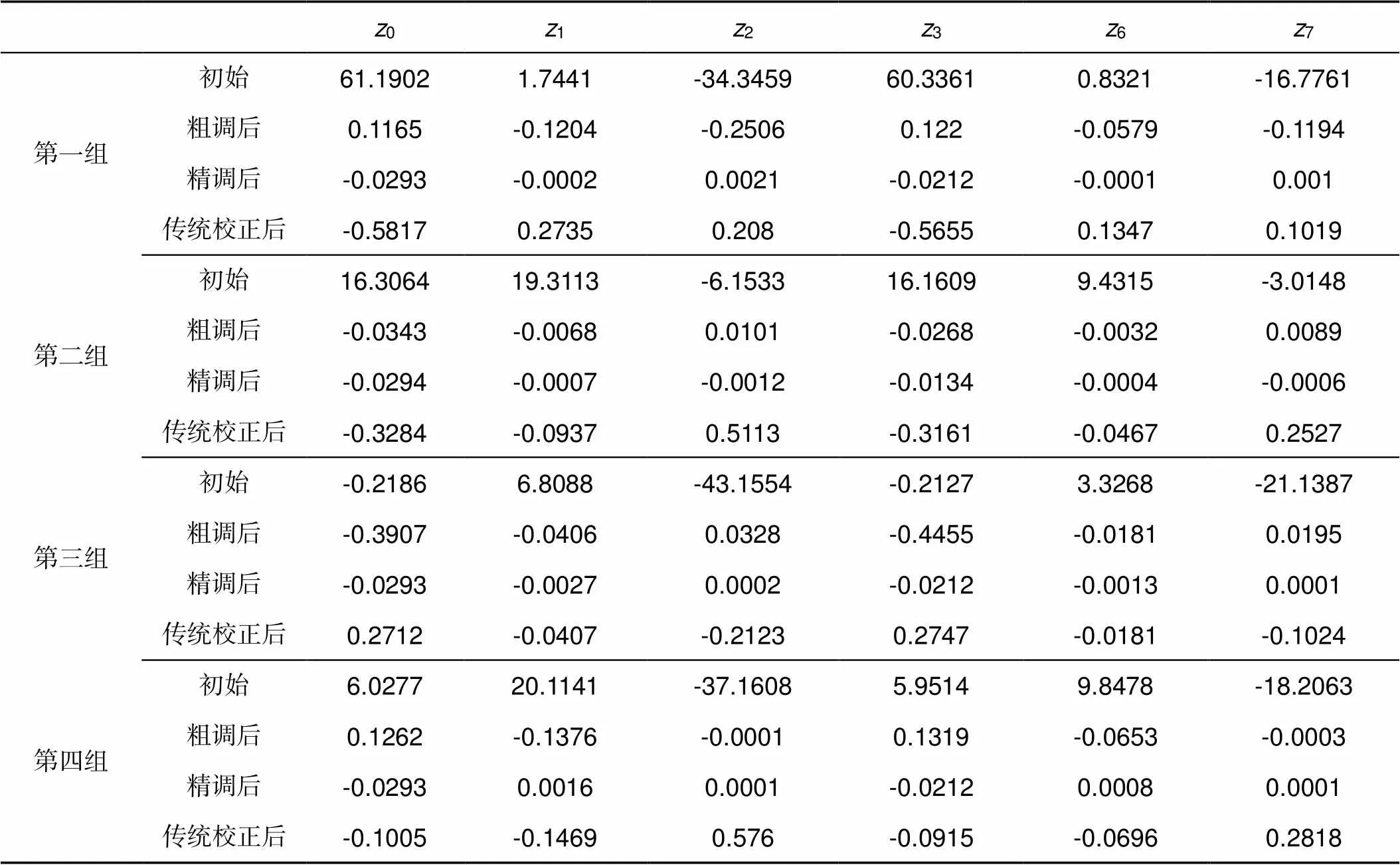
表8 校正前后的泽尼克系数

[1] Zhou L F. Study on the alignment technique of large aperture reflecting telescope on-line[D]. Chengdu: University of Chinese Academy of Sciences (Institute of Optics and Electronics), 2016.

周龙峰. 大口径反射式望远镜在线调整技术研究[D]. 成都: 中国科学院研究生院(光电技术研究所), 2016.

[2] Figoski J W, Shrode T E, Moore G F. Computer-aided alignment of a wide-field, three-mirror, unobscured, high-resolution sensor[J]., 1989, 1049: 166.

[3] Egdall I M. Manufacture of a three-mirror wide-field optical system[J]., 1985, 24(2): 242285.

[4] Gong D, Tian T Y, Wang H. Computer-aided alignment of off-axis three-mirror system by using Zernike coefficients[J]., 2010, 18(8): 1754–1759.

巩盾, 田铁印, 王红. 利用Zernike系数对离轴三反射系统进行计算机辅助装调[J]. 光学精密工程, 2010, 18(8): 1754–1759.

[5] Yang X F. Study on the computer-aided alignment of three-mirror optical system[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2005.

杨晓飞. 三反射镜光学系统的计算机辅助装调技术研究[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2005.

[6] Kim S, Yang H S, Lee Y W,. Merit function regression method for efficient alignment control of two-mirror optical systems. [J]., 2007, 15(8): 5059–5068.

[7] Wang B, Jiang S L. Study on computer-aided alignment method of Cassegrain system[J]., 2008, 30(1): 50–54.

王彬, 蒋世磊. 卡塞格林系统计算机辅助装调技术研究[J]. 光学仪器, 2008, 30(1): 50–54.

[8] Sun J W, Lv T Y, Yao L S,. Design and assembly of transmitter-telescope[J]., 2014, 22(2): 369–375.

孙敬伟, 吕天宇, 姚丽双, 等. 发射望远镜的设计与装调[J]. 光学精密工程, 2014, 22(2): 369–375.

[9] Zhang X M, Jiang F, Kong L Y,. Research on optical alignment technology for Cassegrain system[J]., 2015, 36(4): 526–530.

张向明, 姜峰, 孔龙阳, 等. 卡塞格林系统光学装调技术研究[J]. 应用光学, 2015, 36(4): 526–530.

[10] Gu Z Y, Yan C X, Li X B,. Application of modified sensitivity matrix method in alignment of off-axis telescope[J]., 2015, 23(9): 2595–2604.

顾志远, 颜昌翔, 李晓冰, 等. 改进的灵敏度矩阵法在离轴望远镜装调中的应用[J]. 光学精密工程, 2015, 23(9): 2595–2604.

Application of two step sensitivity matrix method in Cassegrain telescope alignment

Cao Yuze1,2, Ma Wenli1*

1Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2University of Chinese Academy of Sciences, Beijing 100049, China

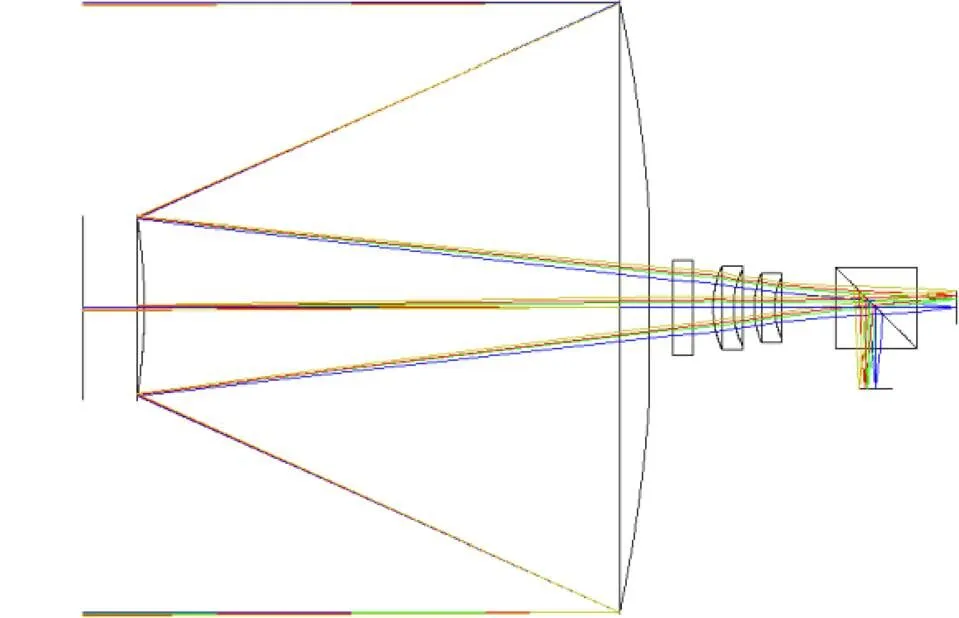
Layout of Cassegrain system

Overview:With the development of telescope technology, the aperture and field of view of telescope are becoming larger and larger, the structure of optical system is becoming more and more complex, and the difficulty of fabrication and assembly is also increasing. The speckle pattern of the focal plane of the optical system can be measured by interferometer and other testing equipment, and the Zernike coefficients can be calculated by the speckle pattern. For Cassegrain telescope, in order to obtain good imaging quality, it is necessary to correct the position of its secondary mirror. By using computer-aided alignment technology, the optical system can be real-time detected and compared with the theoretical results. By establishing a mathematical model between Zernike coefficient and misalignment, the misalignment of the components can be corrected accurately. The most widely used computer-aided alignment method is the sensitivity matrix method. Sensitivity matrix method is a method of correcting aberration by establishing mathematical model of misalignment and Zernike coefficient on the basis of analyzing aberration characteristics. The traditional sensitivity matrix method only carries out single correction. According to the meaning of Zernike coefficient,3、4、5、6、7and8are chosen to construct the sensitivity matrix. Based on the analysis of the shortcomings of the traditional sensitivity matrix method of the two order model, a fine tuning step was added based on the characteristics of the sensitivity matrix. The calculation method of sensitivity is improved. According to the relationship between misalignment and Zernike coefficient, the selection principle of Zernike coefficient for constructing sensitivity matrix is proposed. The traditional sensitivity matrix method is improved. For the Cassegrain system, the relationship between the Zernike coefficients and the misadjustment was analyzed, and the calibration simulation of Cassegrain system with 300 mm aperture and 0.6° field of view was carried out. The simulation results show that after correction by traditional sensitivity matrix method, the mean values of offset along,,axes and tilt around,axes are -0.0684 mm, -0.0892 mm, 0.0015 mm, 0.0498° and -0.0444°, respectively, and the full field wavefront aberration RMS is less than 0.1(=632.8 nm). After correction by two step sensitivity matrix correction method, the mean values are -0.0018 mm, -0.0012 mm, 0.0002 mm, 0.0008° and -0.0012°, respectively, and the full field wavefront aberration RMS is less than 0.03. The corrected optical system reaches the diffraction limit and approaches the design position, which is obviously superior to the traditional sensitivity matrix method.

Citation: Cao Y Z, Ma W LApplication of two step sensitivity matrix method in Cassegrain telescope alignment[J]., 2020, 47(2): 180536

Application of two step sensitivity matrix method in Cassegrain telescope alignment

Cao Yuze1,2, Ma Wenli1*

1Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2University of Chinese Academy of Sciences, Beijing 100049, China

In order to adjust the position of the secondary mirror of Cassegrain telescope with large field of view, a computer aided adjustment method of two-step sensitivity matrix model was proposed. Based on the analysis of the shortcomings of the traditional sensitivity matrix method of the two order model, a fine tuning step was added based on the characteristics of the sensitivity matrix and the traditional sensitivity matrix method was improved. For the Cassegrain system, the relationship between the Zernike coefficients and the misalignment was analyzed, and the calibration simulation of Cassegrain system with 300 mm aperture and 0.6° field of view was carried out. The simulation results show that after correction by traditional sensitivity matrix method, the mean values of offset along,,axes and tilt around,axes are -0.0684 mm, -0.0892 mm, 0.0015 mm, 0.0498° and -0.0444°, respectively, and the full field wavefront aberration RMS is less than 0.1(=632.8 nm). After correction by two step sensitivity matrix correction method, the mean values are -0.0018 mm, -0.0012 mm, 0.0002 mm, 0.0008° and -0.0012°, respectively, and the full field wavefront aberration RMS is less than 0.03, which is obviously superior to the traditional sensitivity matrix method.

aberration correction; sensitivity matrix method; computer-aided alignment; Cassegrain system

TH743

A

10.12086/oee.2020.180536

: Cao Y Z, Ma W L. Application of two step sensitivity matrix method in Cassegrain telescope alignment[J]., 2020,47(2): 180536

2018-10-22；

2019-03-13

曹宇泽(1994-)，男，硕士研究生，主要从事大口径望远镜的像差检测与校正方面的研究。E-mail：qfwxdc@163.com

马文礼(1962-)，男，研究员，博士生导师，主要从事光电探测、精密机械、光电探测系统总体技术的研究及大型光电望远镜的研制。E-mail：mawenli@ioe.ac.cn

曹宇泽，马文礼. 两步式灵敏度矩阵法在卡塞格林望远镜装调中的应用[J]. 光电工程，2020，47(2): 180536

* E-mail: mawenli@ioe.ac.cn