一种基于综合模型的GPS高程优化方法

惠振阳， 程朋根， 鲁铁定， 王乐洋， 胡海瑛

(1.东华理工大学 江西省数字国土重点实验室，江西 南昌 330013；2.流域生态与地理环境监测国家测绘地理信息局重点实验室，江西 南昌 330013；3. 东华理工大学 测绘工程学院，江西 南昌 330013)

自GPS问世以来，由于其速度快、效率高、操作简便等特点而备受人们青睐。如今，GPS已广泛应用于各种工程测量中。通过GPS网平差，已经可以得到精度达10-6～10-9(张前勇等，2006)甚至更高的平面坐标，该精度已能很好地满足工程测量的要求。在GPS网中，如果有一点或者多点在WGS-84坐标体系下，通过平差同样可以得到精度比较高的GPS各点的大地高程。

但是，在实际测量中，往往通过水准测量得到高程值而很少用GPS。这是因为测量中所需要的高程是正常高Hr，是地面点沿铅垂线至似大地水准面的距离。而通过GPS测量所得到的高程是大地高H84，是地面点沿参考椭球面的法线方向到参考椭球面的距离(邸国辉等，2016)。在忽略垂线偏差的前提下，两者有如下关系(徐绍全等，2009)：

Hr=H84-ζ

(1)

ζ为高程异常，表示似大地水准面至椭球面间的高差。其相互关系如图1所示：

从上述关系可以看出，为实现GPS大地高向正常高的转换，就必须求得各点的高程异常ζ。求高程异常的方法有重力法、数学模型法以及神经网络法。然而重力法需要精确的重力数据，在我国精确的重力值是保密数据，且经实验对比单凭重力数据不能获得高精度的高程异常(谢忠俍，2017)，故本次主要讨论的是数学模型法。

GPS高程转换数学模型法有很多，比如加权均值法、多项式曲面拟合法。加权均值法的基本思想是通过待定点周围已知点高程异常的加权平均求得该点的高程异常。多项式曲面拟合法的基本思想是由曲面内已知点的高程异常应用数学曲面拟合而求得待定点的高程异常(陈安平等，2013)。金时华(2005)利用一个复杂无规则曲面可由多个规则曲面表示的数学思想，用二次曲面拟合法拟合出多个曲面，将多个曲面拼接成一个整体从而求取其高程异常。车建仁等(2016)使用了切比雪夫多项式对高程异常进行内插计算，所获得的高程异常相较于平面模型、曲面模型以及多面函数模型具有较高的内符合精度和外符合精度。郭辉(2018)将二次项曲面模型和RBF神经网络组合成一个新的模型，实验证明该模型可行，且较单一的二次项曲面模型和RBF神经网络模型而言，精度有较大的提升。刘斌等(2016)提出将EGM2008模型与二次曲面拟合模型结合的组合模型求解高程异常，实验结果表明，可提高GPS高程拟合的精度。

传统的加权均值法不适合在大范围测区使用，其求出的高程异常可能超出误差限。多项式曲面拟合法在一定程度上拟合出高程异常的趋势面，但不能很好地与实际数值贴近，并且对应用的地形和控制点分布有要求(孙佳龙等，2013；罗陶荣等，2018)。为了解决上述问题，笔者提出了一种融合加权均值法和多项式拟合法的GPS高程转换综合模型。这种模型主要是在多项式拟合模型的基础上加上地形改正，从而使其在高程异常起伏较大的区域同样能达到较高的拟合精度。

1 改进的综合模型方法

一般地，可将待定点的高程异常表示为(钟波等，2007)：

ζ=ζ0+ζr

(2)

式中，ζ0为ζ的主项，称为高程异常的长波部分；ζr为ζ的副项，称为高程异常的短波部分。ζ0可通过多项式曲面拟合求出，而ζr则主要是地形改正，可由加权均值法求出，继而相加可得到待定点的高程异常。

1.1 建立多项式曲面模型并对其做显著性检验

按上述方法建立多项式拟合方程，并对其作F统计量的假设检验。

H0∶β1=β2=…βp=0；H1:至少有一个βi≠0,1≤i≤p

其中βi为拟合方程各项系数。当H0为真时，F～F(p，n-p-1)，给出显著性水平α(通常取为0.1)，可通过查表得到其临界值Fα(p，n-p-1)，由观测量可计算出对应的F0(向东进等，2005)。

F0≤Fα(p，n-p-1)，则接受H0；F0>Fα(p，n-p-1)，则拒绝H0。

若检验的结果是接受H0，则表明相较于模型的误差，自变量对因变量的影响是不显著的。此时所建立的回归模型不能很好地预测待定点的高程异常，需要检查是否缺少重要的自变量，再重新建立新的模型。

1.2 回归系数的显著性检验

即使回归方程通过了显著性检验，并不意味着每个自变量对因变量有显著的影响，其中可能某个xi(=1,2,…,p)对因变量的影响是不显著的。要剔除这些不显著的自变量，进而建立一个更为简单有效的回归模型。对回归系数做显著性检验，将不能通过显著性检验的自变量剔除。

首先做出检验假设：

H0∶βi=0，H1∶βi≠0

对各项系数作t统计量假设检验，当|ti|>tα/2(n-p-1)时，拒绝H0；反之，接受H0。若接受H0则表示βi对方程的影响是不显著的，舍弃该项。

经过回归系数的显著性检验，可得到一个拟合优度较好的回归方程模型，用此模型可计算得到较精确的高程异常长波部分ζ0。

1.3 计算地形改正ζr

(1)按上述方法建立一个拟合精度较好的回归模型，分别计算出各个拟合点高程异常长波部分ζ0，则ζr=ζ-ζ0

(2)对测区各个拟合点进行聚类。选择一些特征点(xi,yi)，称之为凝聚点，按照下列原则：

(xj-xi)2+(yj-yi)2≤R2

(3)

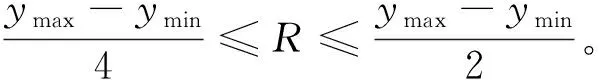
(3)求待定点ζr。根据待定点的实际点位，确定其属于某个凝聚点的聚类，在其聚类中按照加权均值的思想即可求出ζr。

最终即可求得待定点的高程异常：ζ=ζ0+ζr。

2 工程实例

本实例数据来自某测区，测区的地形如图2。测区的控制点分布如图3，选取GPS控制网中36个与水准点重合的点，其中30个为拟合点，6个为检核点。

为避免病态法方程的出现，致使求解过程不稳定，计算前需先对x，y坐标数据进行中心化处理，即每个坐标数据都减去它的平均值(陶本藻，2007)。

对所测区域进行最高二次拟合，即所列全模型为：

(4)

然后对其进行回归方程的显著性检验，实例计算结果得：

F0=72.891>F0.1(5,24)=2.10

故全模型的整体效果是显著的，继而对回归方程各系数进行显著性检验，实例计算结果得：

|t1|=4.013>t0.1/2(24)=1.711

|t2|=8.257>t0.1/2(24)=1.711

|t3|=5.741>t0.1/2(24)=1.711

|t4|=3.896>t0.1/2(24)=1.711

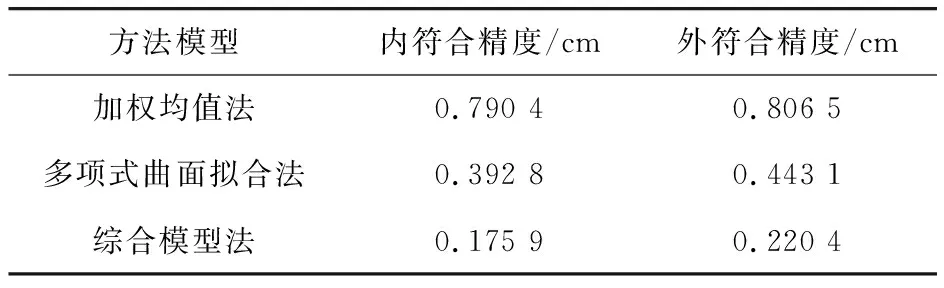
|t5|=1.013

由此可以看出，交叉项xy的系数没能通过显著性检验，故选用式(5)选模型：

(5)

用此选模型依次计算各拟合点的高程异常，同时计算出各拟合点的地形改正ζ0。本测区选择四个凝聚点(大圆)进行聚类(图3)。

再按照加权均值的方法对上述四个大圆内的检核点进行高程异常拟合计算，验证其精度。

3 实验分析

本次采用加权均值法、多项式曲面拟合法以及笔者所提出的综合模型方法分别计算上述工程实例中的拟合点(图4)以及检核点(图5)的残差并进行对比。图5显示的是各个拟合点的残差对比结果。从图中可以看出，相较于多项式曲面拟合法和加权值拟合法，本文所提出的综合模型法能取得更小的拟合误差。此外，从图5中可以看出本文方法的拟合误差在各个点上的误差波动较小，因此可以得出本文方法具有较强的鲁棒性。图6为检核点的残差对比。从图中可以看出，相较于其他两种方法本文方法在6个点位均能取得更小的残差。因此，本文方法能够取得更好的拟合结果。

为客观地评定三种模型的精度，以便于在实际应用中选取最优模型，分别计算三种模型的内符合精度以及外符合精度(张兴福等，2003)，如表1所示。从表1中可以看出，本文方法无论是在内符合精度还是外符合精度均能取得更小的拟合误差。三种方法对比结果显示，加权均值法效果较差，在内符合精度和外符合精度上均无法取得较好的拟合效果。此外，还可以发现三种方法的内符合精度均要优于外符合精度。这主要是因为计算内符合精度时是依据拟合点进行计算的，所以误差相对会比较小；而外符合精度则是对检核点进行计算的，所以误差会相对较大。

表1 不同拟合方法的拟合精度

4 结论

由上述计算结果可知，在范围较小且较平坦的区域，三种模型都能得到较好的拟合结果。加权均值模型思路简单且便于计算，但是若在大范围测区采用此方法，拟合精度不是很好。这种模型方法依赖于测区内已知水准点的个数，若个数较少且分布不均，计算结果很可能不能通过限差要求。多项式曲面拟合模型是按照削高补低的原则拟合出一个曲面来近似地代表似大地水准面，在平坦的起伏不大的区域能得到很好的拟合结果。高程异常变化较大的区域，拟合结果较差。综合模型采取了上述两种模型的思想，将高程异常分为长波部分和短波部分，然后对其分别计算。结果显示该模型不仅适用于平坦区域，而且在高程异常变化较大的区域也能得到较好的拟合精度。