具有非局部条件的时间分数阶热传导方程的Chebyshev小波数值方法
许小勇, 熊临晨
(东华理工大学 理学院,江西 南昌 330013)
非局部条件主要出现在边界数据无法直接测量的情况下,具有非局部条件的边值问题具有非常重要的应用,最近具有非局部条件的分数阶热传导方程得到了大量的关注。Ashyralyev等(2003)利用半群方法求解了一维经典的具有非局部条件的热传导方程并分析方法的稳定性。Zhou等(2009)提出了基于再生核方法求解经典的具有非局部条件的抛物型方程。然而利用数值方法讨论含非局部边界条件分数阶热传导方程的文献很少见报道。Karatay等(2011)利用基于改进的高斯消去法求解了非齐次非局部分数阶热传导方程;Bhrawy等(2014)应用Legendre Tau方法求解了此问题。
小波分析理论产生于1980年代初,其思想来源于Fourier分析,但克服了Fourier分析时频不能同时局部化的缺陷, 是Fourier分析理论和应用的发展,在工程中具有非常重要的应用(张晓峰等,2016)。由于小波方法可以同时具备较强的空间和频谱分析能力,有利于高效的得到高精度解。在数学上由正交多项式通过伸缩、平移得到的正交小波近年来被广泛应用于各类方程的数值计算, 如:Legendre小波、Chebyshev小波、Bernoulli小波等(Ali et al.,2017;郑明等,2017;Rahimkhani et al.,2017)。利用第二类Chebyshev小波求解如下具有非局部条件的分数阶热传导方程:
(1)
非局部条件和边值条件
u(x,0)=u(x,1)+f(x),0 (2) u(0,t)=g0(t),u(1,t)=g1(t),0 (3) 其中0<α<1,u(x,t)是关于x和t的温度函数,q(x,t)为已知源项。本研究主要目的是提出一种高精度的数值方法求解方程(1),该方法是基于第二类Chebyshev小波分数阶微分和积分公式并结合小波配置法,将所求解问题转化为代数方程组求解,给出了数值例子并与相关结果进行了比较。 Chebyshev小波ψn,m(x)=ψ(k,n,m,x)包含4个参数,在[0,1)区间上的定义如下: (4) (5) ψn′,m′(y) 对上式进行截断可得, (6) 本次所提算法中需要用到第二类Chebyshev小波函数任意分数阶积分公式,具体如下: 定理1 (Zhou et al.,2017)定义在区间[(n-1)/2k-1,n/2k-1]上第二类Chebyshev小波函数ψn,m(x)的任意a(>0)阶积分计算公式如下: Iαψn,m(x)= (7) 根据Caputo分数阶导数的定义,给出第二类Chebyshev小波函数任意分数阶微分公式。Caputo分数阶导数定义(Podlubny, 1999)如下: 定理2 定义在区间[(n-1)/2k-1,n/2k-1]上第二类Chebyshev小波函数ψn,m(x)的任意α(0<α<1)阶微分计算公式如下: Dαψn,m(x)= (8) 为了描述方便,引入下面的记号 因此,第二类Chebyshev小波函数可表示成 所以,Dαψn,m(x) (9) 对方程(9)中变量从0到x进行两次积分,可得 (10) =(I2Ψ(x))TUΨ(t) (11) 在方程(11)中令x=1,得 (12) u(x,t)=(1-x)g0(t)+xg1(t) +((I2Ψ(x))T-x(I2Ψ(1))T)UΨ(t) (13) 对u(x,t)中变量t求α次导数,得 +((I2Ψ(x))T-x(I2Ψ(1))T)UDαΨ(t) (14) 在实际计算中I2Ψ(1)≈I2Ψ(1-10-15),根据配置法,为了计算方程(9)中的未知系数矩阵U,选取如下配置点 xi=(2i-1)/(2kM),tj=(2j-1)/(2kM),i=1,2,…,2k-1M,j=1,2,…,2k-1M-1。将表达式(9)、(14)代入方程(1)中,并考虑上述配置点,得到2k-1M×(2k-1M-1)个线性方程 (1-xi)Dαg0(tj)+xiDαg1(rj)+((I2Ψ(xi))T-xi(I2Ψ(1))TUDαΨ(tj)-ΨT(xi)UΨ(tj) =q(xi,tj) (15) 另外考虑非局部边值条件,将配置点xii=1,2,…,2k-1M代入方程(2),可得2k-1M个方程 u(xi,0)=u(xi,1)+f(xi) (16) 由此可以得到含2k-1M×2k-1M个变量的线性方程组,求此方程组可解出系数矩阵U,将U代入u(x,t)的表达式(13)中,便可求得方程(1)的近似解。 0 非局部条件u(x,0)=u(x,1)-ln(1+x(1-x)),0 方程精确解为u(x,t)=t2ln(1+x(1-x))。 Bhrawy等(2014)应用Legendre tau-谱方法求解了此问题,并给出了α=0.45和0.95时不同参数N,M情况下的最大绝对误差(MAEs)。表1给出了α=0.45和0.95的最大绝对误差,并与Bhrawy的结果进行了比较。图1分别画出了k=1时,M=10,α=0.45(图1a)和M=12,α=0.95(图1b)的整体误差函数图。为了说明所提出方法的收敛性,笔者画出了当k=1,α=0.45,0.95时最大绝对误差的半对数曲线图(图2),可以看出误差呈指数递减,这也是期待的谱精度。本研究的方法比Bhrawy介绍的方法结果更精确。 例2 考虑如下具有非局部条件的时间分数阶热传导方程 +4π2t2sin(2πx),0 非局部条件u(x,0)=u(x,1)-sin(2πx),0 表1 k=1时不同M值下最大绝对误差值 Bhrawy等(2014)应用Legendre tau方法求解了此问题,为了进一步说明本次算法比文献结果更精确,在表2中比较了两种算法的最大绝对误差值,表明在参数相同的情况下,本次结果具有更高的精度。 表2 k=1时不同M值下最大绝对误差值 在Caputo分数阶导数定义下,利用移位的第二类Chebyshev 多项式解析形式,推导了第二类Chebyshev小波函数的任意α(0<α<1)阶微分公式。建立了一种求解具有非局部条件的分数阶热传导方程有效的小波配置法。通过使用有限数量的小波基函数就可以得到较高精度的解。所给全局误差与多项式次数的半对数曲线图说明本研究方法具有指数收敛特点。所得数值结果与精确解和Legendre tau方法近似解的比较,说明了本次所提方法的有效性。1 第二类Chebyshev小波及性质
2 第二类Chebyshev小波函数任意分数阶微分公式
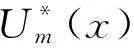


3 算法描述
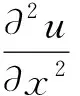
4 数值算例


5 结论

