机械波多解性的一般解法

王云 宋万松

摘要：机械波的多解性问题是机械波的核心考点之一，解决多解性问题的关键在于分析引起多解性的原因，然后利用“去整留零”“分类讨论”“画图找点”各个突破。

关键词：机械波;多解;高考

机械波多解性问题是最近几年高考的一个高频考点，引起机械波多解性的主要因素有时间周期性、空间周期性;传播方向双向性、振动方向双向性;波形的隐含性，对于引起机械波多解性的不同因素需要采用不同的思想、方法进行处理，机械波多解性能很好地考查逻辑思维的严谨性，本文结合实例总结此类问题的一般思维方法。

1“去整留零”研究周期性

机械波与生俱来的特点是具有周期性，空间周期性用波长λ来表达，时间周期性用周期T来体现，空间周期性与时间周期性具有对应关系，经过半个周期，波传播半个波长;波传播四分之三个波长，需要四分之三个周期，这种时空对应正是物理的精髓思想之一，由于时间周期性、空间周期性引起的机械波的多解，可以采用“去整留零”的思想进行处理，可以先考虑一个周期T内的△t、一个波长λ内的△x情况，然后再考虑周期性构建时间的关系t=nT+△t，空间的关系x=nλ+△x。

2“分类讨论”考虑双向性

如果没有告知波源的位置等相关信息，无法确定机械波的传播方向以及介质中质点的振动方向，这样分析过程存在不确定因素，通常采用假设、分类、讨论的思维流程，

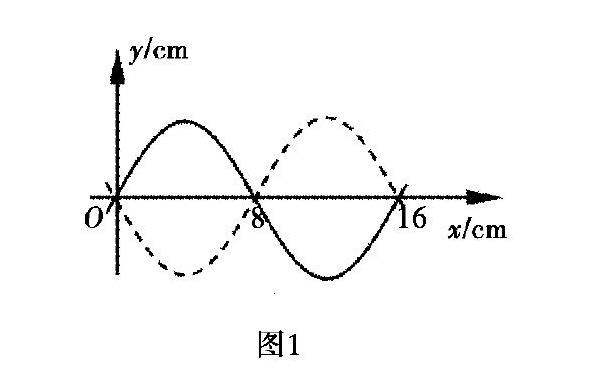
例2如图2所示是一列沿x轴传播的机械波图像，实线是t1=o时刻的波形，虚线是t2=1s时刻的波形，求这列波的周期和波速，

分析与解：虽然题干明确机械波沿x轴传播，但没有告知向左还是向右传播，情况不确定，采用假设、分类、讨论。

3“画图找点”突破隐含性

题干仅提供几个特殊点的相关信息，对于波形图其他相关信息均处于隐含状态，引起波形图有多种可能，解题过程需要把隐形的条件利用“画图找点”的思想得以显性的呈现。

例4如图4所示，一列简谐横波向右传播，P、Q两质点平衡位置相距0.15m，当P运动到上方最大位移处时，Q刚好运动到平衡位置且向下运动，则这列波的波长可能是多大？

分析与解题干虽然提供了p、Q两质点的相关信息，但未告知P、Q两质点问的具体波形图给解题带来不确定性，利用“画图找点”进行抽丝剥茧，层层推进，寻找问题的突破口。

第一步：如图5画一条正弦曲线，虚线代表介质中各质点的平衡位置。

引起机械波多解的原因通常不是单一因素引起，往往是三方面因素共同造就，解题过程明确引起多解性的原因，选择合适的思想、方法逐一突破。

例5在一列简谐横波传播的路径上有A、B两质点，两质点的振动图像如圖6甲、乙所示，A、B两质点问的距离为2m，求波传播的速度。

分析与解题干仅仅告知A、B两质点的振动图像，波的传播方向不确定，A、B两质点问的波形图不确定，同时还需要考虑波形图的空间周期性，这些共同的不确定性造成波的传播速度具有多解性，利用以上分析的思维方法进行逐一突破。

第一步：设简谐横波从A向曰传播，t=0时刻质点A在平衡位置且向下运动，质点B在正向最大位移处，采用“画图找点”确定两点问的最简单波形图，如图8发现A、B两质点问的最简单波形是四分之一波长。

第四步：设简谐横波从B向A传播，t=0时刻质点A在平衡位置且向下运动，质点B在正向最大位移处，采用“画图找点”确定两点问的最简单波形图，如图7发现A、B两质点问的最简单波形是四分之三波长。

总结：机械波的多解性问题是机械波的核心考点之一，具有一定的综合性和区分度，解决多解性问题的关键在于分析引起多解性的原因，然后分别利用“去整留零”“分类讨论”“画图找点”各个突破。