高中物理竞赛中天体运动问题的处理探讨

姜胜 杨春芳

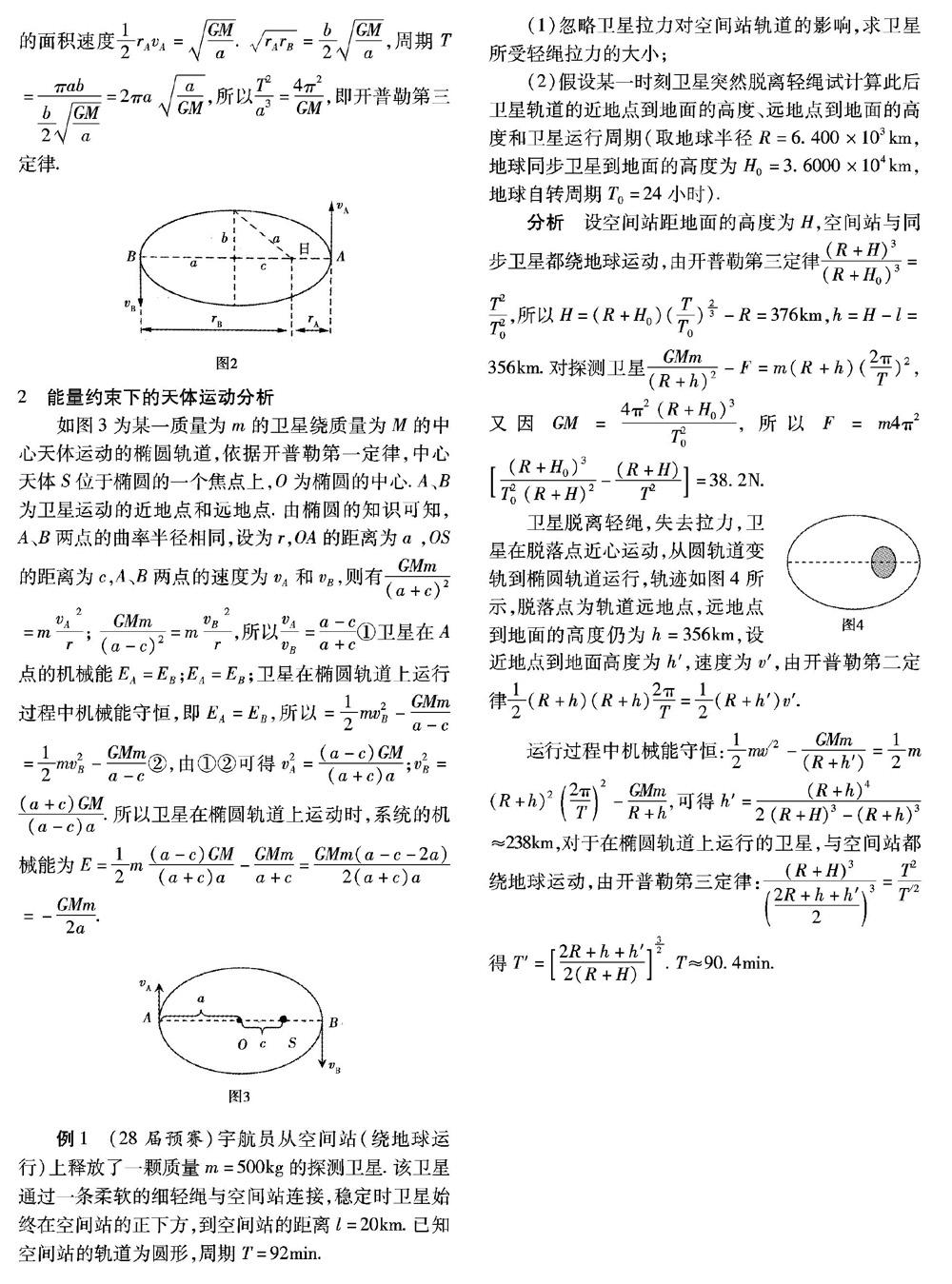
摘要：椭圆轨道上的天体运动问题，历年来一直是高中物理竞赛的必考点和难点，本文试图梳理椭圆轨道上天体运动的基本规律，提出解决此类问题的基本方法。

关键词：三大定律;椭圆轨道;面积速度;角动量守恒;极坐标

浩瀚的宇宙，天体的运动复杂多变，但它们都在“三大定律”的约束下和谐地运动着，为我们呈现出一幅绝美的“星空印象”，这“三大定律”即为：开普勒行星运動定律、牛顿运动定律和机械能（能量）守恒定律，近些年的高中物理竞赛中，天体运动考查频繁，更多的是要求学生分析椭圆轨道上的天体运动，下面就来谈谈解决此类问题的基本方法。

1轨道约束下天体运动分析

例2（35届复赛）假设地球是一个质量分布各向同性的球体，地球自转及地球大气的影响可忽咯从地球上空离地面高度为h的空间站发射一个小物体，该物体相对于地球以某一初速度运动，初速度方向与其到地心的连线垂直，已知地球半径为R，质量为M，引力常量为G，（1）该物体能绕地球做周期运动，其初速度的大小应满足什么条件？

（2）该物体的初速度大小为Vo，且能落到地面，求其落地时速度的大小和方向（即速度与其水平分量之间的夹角），以及它从开始发射至落地所需的时间。

椭圆轨道天体运动一直是高中物理竞赛的考查热点，常规研究主要集中在天体在椭圆轨道上运动的能量、速度、高度和变轨问题，此类问题主要借助“三大定律”和角动量守恒分析解决，复杂研究主要是部分椭圆（或抛物线）轨道上天体的运动时间问题，基本思路是依据物理规律找出矢径r与运动时间t微分关系，再对两者积分得出时间。