过冷沸腾多相流模拟及发动机冷却结构研究＊

张俊红 徐喆轩 王静超 徐天舒 林泽峰 马梁

（天津大学，内燃机燃烧学国家重点实验室，天津 300072）

主题词：发动机 过冷沸腾 多相流 相间模型 冷却结构

1 前言

发动机冷却系统直接影响发动机的热负荷水平，其性能的优劣对整机的动力性、经济性和排放性能具有重要影响。发动机冷却水腔结构复杂，内部结构不可见，导致设计难度较大，常用的试验方法难以应用，因此采用计算流体力学（Computational Fluid Dynamics，CFD）对其进行优化设计受到研究人员的广泛关注。传统无相变CFD的方法由于采用显热代替潜热的方式，准确性不高，而考虑相变的多相流CFD模拟可以表征潜热吸热的过程，准确地模拟流体温度场。

傅松[1]分别采用对流传热修正传热系数的方法和均匀多相流沸腾传热模型建立了用于缸盖冷却通道内沸腾传热计算的修正算法；Arash[2]采用两相的Mixture多相流模型对柴油机冷却通道进行模拟，得到冷却通道内压力、温度、体积分数的分布；谷芳[3]利用流体体积（Volume of Fluid，VOF）两相流方法建立过冷沸腾模型，采用T型管和铸铝缸盖进行试验验证，模型适应性很高；花仕洋[4]采用欧拉（Eulerian）多相流模型对单缸发动机缸盖进行模拟，与无相变对流传热结果对比，Eulerian模型计算结果更准确；张俊红[5]采用混合（Mixture）多相流模型简化复杂的过冷沸腾问题，提高了计算准确性。上述发动机冷却通道的传热仿真研究都将多相流与对流传热进行比较，以证明仿真的准确性，但由于研究中采用的多相流模型多种多样，因而无法说明哪一种模型更适合发动机冷却通道的过冷沸腾模拟。

为准确选择多相流模型，本文针对某发动机冷却通道中的过冷沸腾现象，建立多种过冷沸腾模型，通过模拟验证和比较建立准确高效的多相流模型，并分析不同结构发动机冷却通道的流动换热现象。

2 多相流模型

换热设备中宏观多相流模拟常用Eulerian模型和Mixture模型，这两个模型同样应用于发动机冷却通道的多相流模拟。

2.1 Eulerian模型

质量方程为：

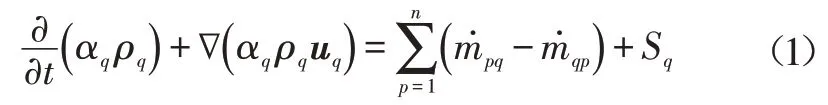
动量方程为：

能量方程为：

式中，αq、ρq分别为q相的体积分数和密度；m pq、mqp分别为p相到q相和q相到p相的质量交换；up、uq分别为p相和q相的速度；uq、uqp分别为p相相对于q相、q相相对于p相的速度；τq为剪切张力；g为重力；∑F为相间作用力之和；hq为q相的焓；∇qq为热通量；Sq为能量的源项；Qpq为换热量；hpq、hqp为潜热；n为相的总数目。

2.1.1 动量交换模型

两相间的作用力十分复杂，一般将其分解：

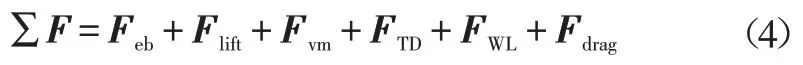
式中，Feb为外部体积力；Flift为升力；Fvm为虚拟质量力；FTD为湍流离散力；FWL为壁面润滑力；Fdrag为曳力，是两相间最主要的力。

升力方程为：

式中，Cl为升力系数；αg为气相体积分数。

虚拟质量力方程为：

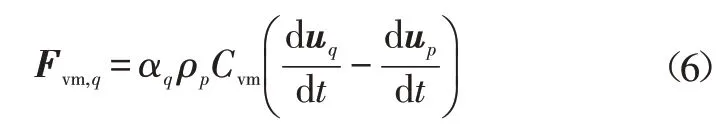
式中，ρp为p相的密度；Cvm=0.5为虚拟质量力系数。

壁面润滑力方程为：

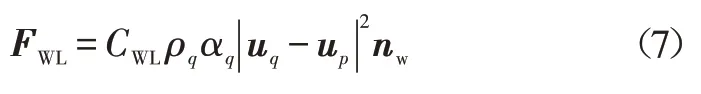
式中，CWL为壁面润滑力系数；nw为指向远离墙壁方向的法向单位距离。

流体对流体的曳力模型方程为：

式中，Δu为两相间的速度差；CD为曳力系数；db为气泡直径。

湍流离散力与曳力关系密切，其方程为：

式中，μtq为动力粘度；δpq=0.75；αp为p相的体积分数。

相间作用力除本身参数外，主要由各力系数决定，部分相间作用力系数模型如表1所示。

表1 部分相间作用力系数模型

2.1.2 内部换热模型

在流场内部，质量交换主要取决于两相的温度、换热系数和潜热，温度决定热量传递的方向，质量交换率为：

式中，αi为界面浓度；hinter为界面处的换热系数；Q为总热量；QT为表热；Tsat为饱和温度；Tl为液相温度；hlg为潜热。

常用的界面换热系数模型有Ranz-Marshall[12]、Tomiyama[10]、Hughmark[13]模型等。Ranz-Marshall引用雷诺数和普朗特（Prandtl）数来表征相间努塞尔数Nu：

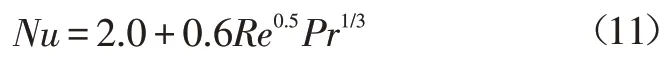
式中，Re为相对雷诺数；Pr为普朗特数。

Tomiyama提出了适用于较低雷诺数流动情况下的换热模型：

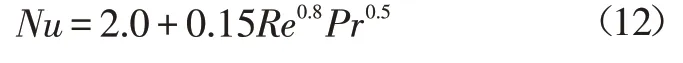
Hughmark拓展了Ranz-Marshall变化范围：

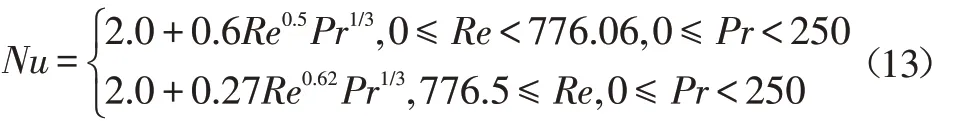
2.1.3 壁面沸腾换热模型

由于两相的运动，流体与壁面形成3种换热形式：气相或液相对壁面的对流换热，其中气相对流换热程度根据气相份额决定，在核态沸腾阶段基本可以忽略；由液相转化成气相的潜热；由于气泡离开壁面形成的气液交替与壁面换热的现象，简称“淬火”换热。3种换热形式如图1所示，根据这3种换热形式得到的壁面换热量计算式为：

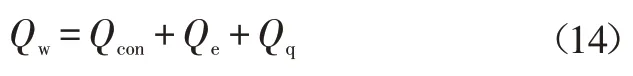
式中，Qw为壁面处总热量；Qcon为对流换热热量；Qe为气相潜热热量；Qq为“淬火”换热热量。

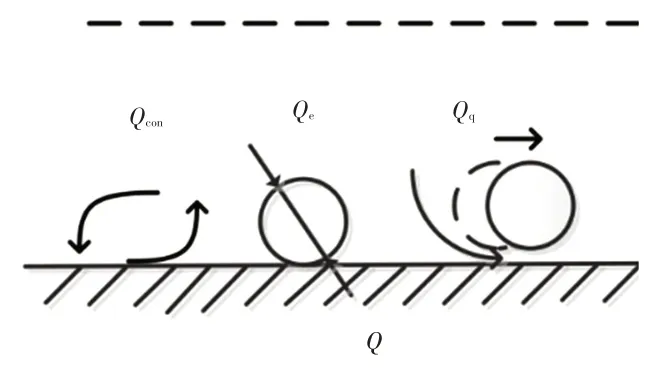
图1 壁面换热形式和气泡运动行为

大量研究以壁面处的气泡脱离直径、气泡脱离频率和气泡核点密度来描述壁面处的沸腾换热程度：

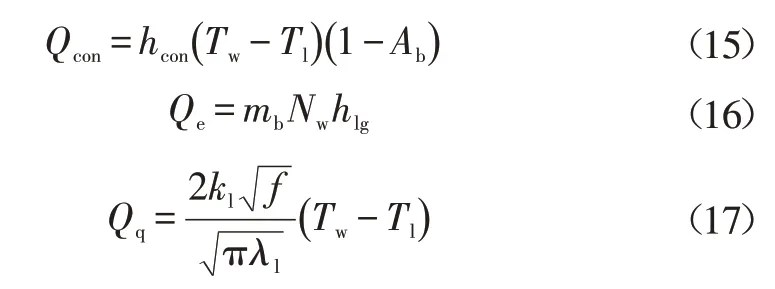
式中，hcon为对流换热系数；Tw为壁面温度；Ab、(1-Ab)分别为气相和液相覆盖的面积；mb为气泡在脱离时刻的质量；Nw为核点密度；kl为液体的导热；f为气泡脱离频率；λl为扩散率。

气泡覆盖面积与气泡脱离直径、核点密度有关：

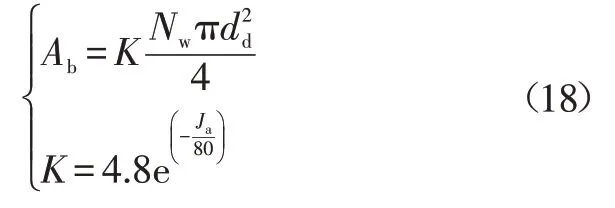
式中，dd为气泡脱离直径；K为经验常数，可由Del Valle and Kenning[14]关联式获得；Ja为雅克比数。

气泡脱离直径、气泡脱离频率和气泡核点密度的部分模型如表2所示。

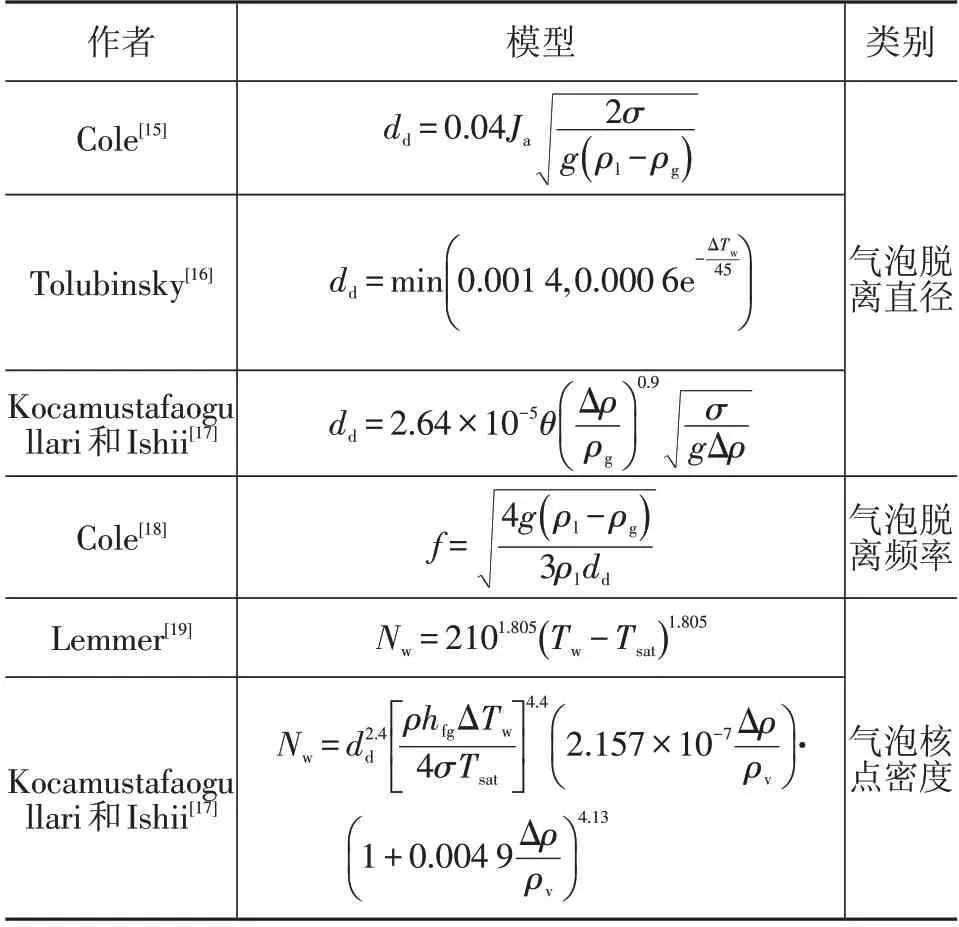
表2 部分壁面沸腾模型

2.2 Mixture模型

混合相质量方程为：

混合相动量方程为：

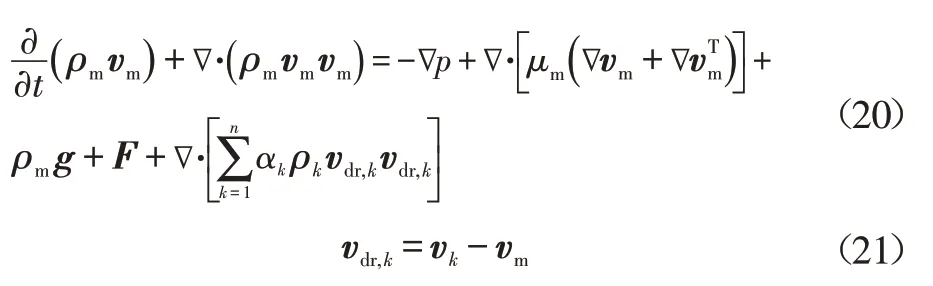
混合相能量方程为：

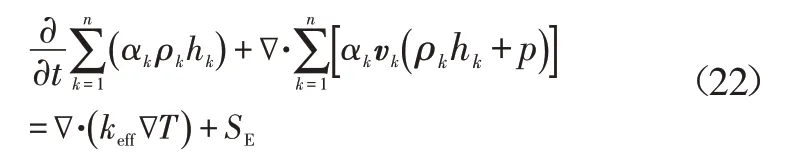
式中，vm为质量加权平均速度；ρm为混合密度；μm为混合相的动力粘度；F为相间力；αk为k相体积分数；ρk为k相密度；vk为k相速度；hk为k相焓；vdr,k为二次相的漂移速度；keff为有效导热系数；T为温度；SE为其他的体积热源。

Mixture模型是对混合相进行求解，再通过滑移速度求解各相。

滑移速度与相对速度的关系为：

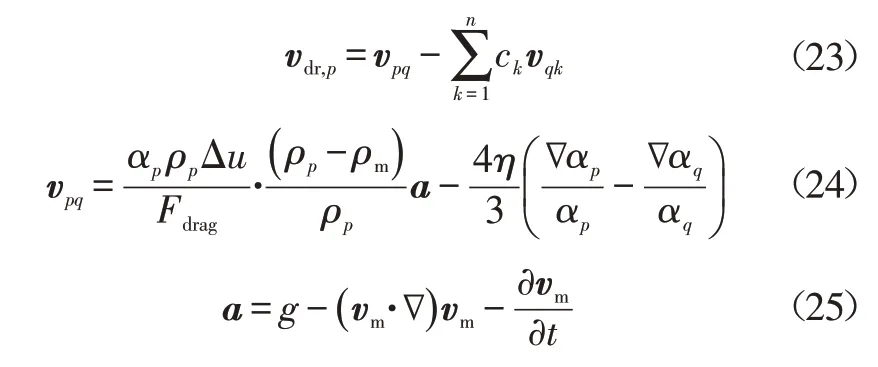
式中，vpq、vqk分别为p相和k相对于主相q的相对速度；ck为k相的质量分数；a为加速度；η为湍流扩散率。

Mixture模型采用平均界面换热系数简化描述多相流的换热过程（包括过冷沸腾），其中Lee[20]模型以热为机理描述蒸发和冷凝过程：

式中，mlv、mvl分别为液相转为气相、气相转为液相的质量；Ccoe为蒸发或冷凝频率；αl、αv分别为液相、气相的体积分数；ρl、ρv分别为液相、气相的密度；Tl为液相温度；M为流体摩尔质量；R为气体常数；hfg为潜热。

2.3 模型筛选流程

对于多相流模型中的子模型，忽略适用范围，约有几百种配合方式。多相流模型在流场模拟应用上的首要问题是如何准确地选取模型。在本文涉及的发动机冷却通道内流场数值模拟中，按模型的重要程度逐步进行筛选，得到最终的多相流模型，多相流模型筛选流程如图2所示。

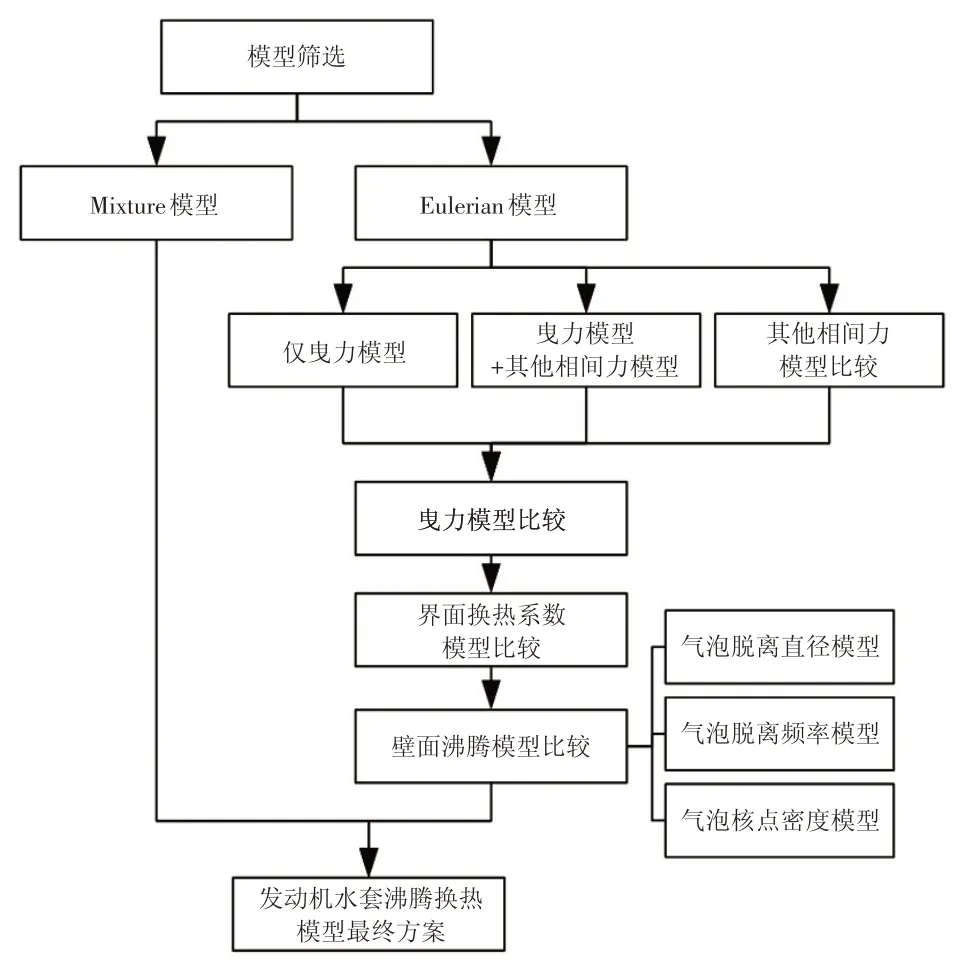
图2 多相流模型筛选流程

3 发动机过冷沸腾仿真

3.1 发动机模型

针对某直列6缸4冲程柴油机，建立其机体和冷却通道的三维几何模型，并简化部分结构生成网格，如图3所示。方案1为原始冷却通道网格模型，用来比较多相流的模拟结果；方案2为在原始冷却通道的基础上，将位于发动机中间的冷却通道入口改到单独一侧，保持出口位置不变，考察流动方向引起的冷却变化；方案3为在原始冷却通道的基础上，切断缸体冷却通道与缸盖冷却通道的联系，将冷却通道改为分离式，缸盖冷却通道入口设在两缸冷却通道之间，在原出口基础上两侧各增加1个小出口，缸体冷却通道入口位置不变，出口设置在缸体两侧，考察缸盖缸体分离冷却的效果。方案1～3作为对比进行发动机冷却通道结构的研究。

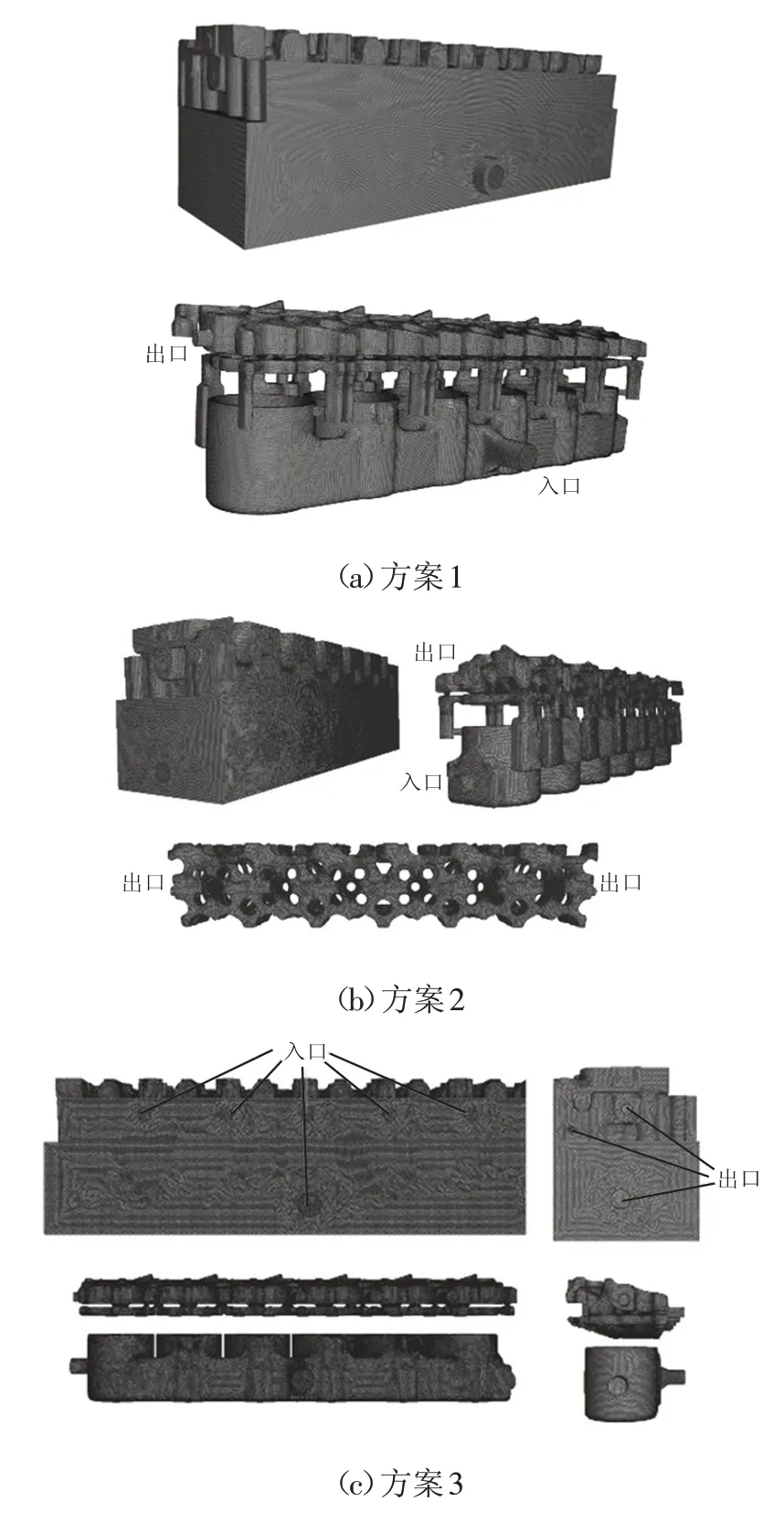
图3 发动机网格模型

3.2 边界条件

根据柴油机厂商提供的热边界条件，考虑发动机缸套换热的不均匀性，将缸套划分为上、中、下3个面，并将热边界条件按面积权重进行修正，计算得到热边界条件如表3所示。冷却液入口温度为363 K，入口流量为15.1 m3/h。模拟中将发动机缸体缸盖和冷却液作为整体，采用流固耦合方法计算固液能量交换，采用k-ε湍流模型进行各相内的湍流计算。

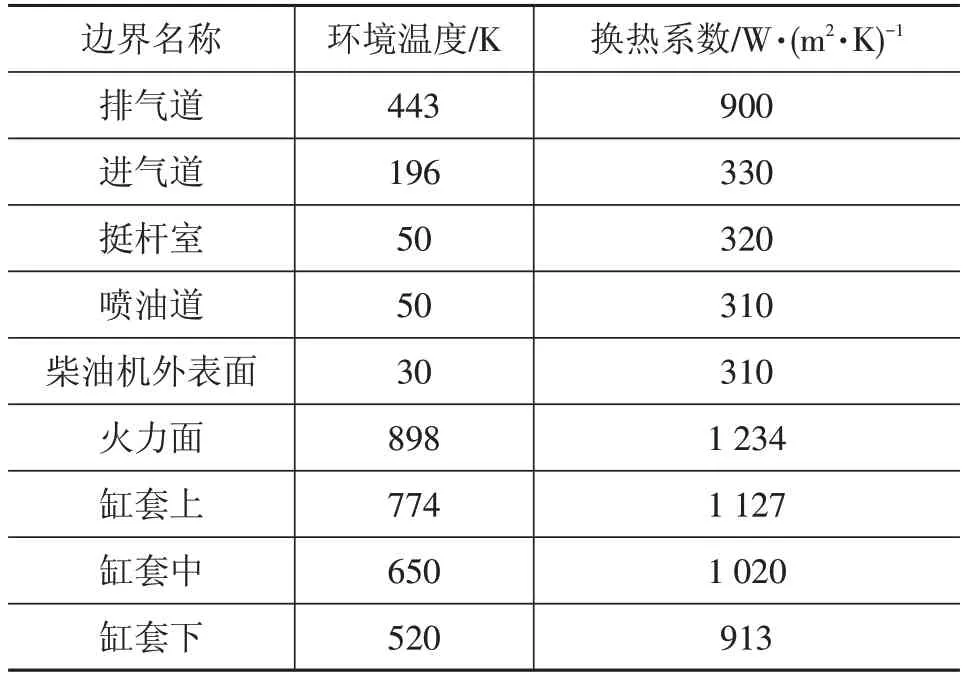
表3 发动机热边界条件

3.3 发动机过冷沸腾仿真结果

3.3.1 曳力系数模型比较

Eulerian多相流模型中选择Tolubinsky的气泡脱离直径模型、Cole的气泡脱离频率模型、Lemmer的气泡核点密度模型组成壁面沸腾换热模型，再选择Ranz-Mar⁃shall的两相间换热系数模型，并将这些模型作为基准模型，以考察不同曳力系数模型在发动机冷却通道中模拟的准确性。不同曳力系数模型的火力面温度仿真结果如图4所示，从温度分布可看出，除Grace模型外，其余模型冷却液入口附近的火力面温度最高，冷却液出口附近的火力面温度最低，这与冷却通道内流量分布一致。

图4 采用不同曳力系数模型的发动机火力面温度仿真结果

为选取最合适的曳力系数模型，利用热电偶对该柴油发动机火力面温度进行测量，测点布置在柴油机火力面和冷却通道出、入口处，如图5所示，火力面温度测量结果如表4所示。将火力面温度分布（图4）与试验测量值（表4）进行对比可发现，采用Schiller and Naumann曳力系数模型的仿真结果与试验测量值最吻合，采用Grace曳力模型计算的温度值过低，采用Tomiyama曳力模型和Ishii曳力模型的计算温度值均过高。因此，本文选取Schiller and Naumann模型作为发动机冷却通道过冷沸腾模拟的曳力系数模型。

图5 发动机温度测点布置

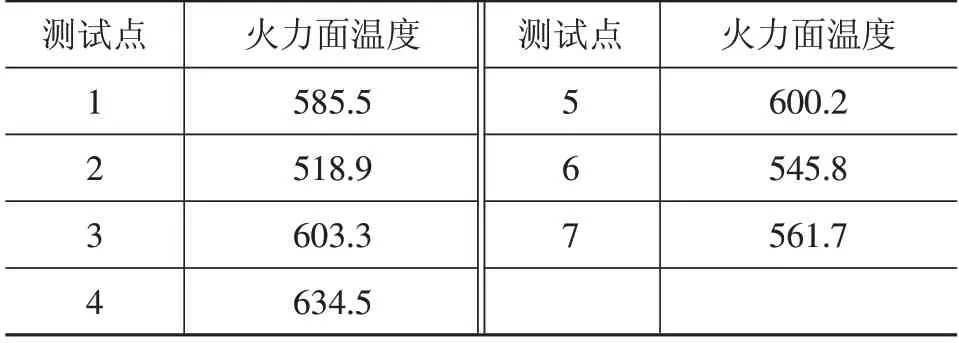
表4 火力面温度测量结果 K

3.3.2 换热模型比较

在采用Schiller and Naumann曳力系数模型的基础上，选取不同界面换热系数模型、气泡脱离直径和气泡核点密度计算发动机火力面温度，部分结果如图6所示。整体而言，界面换热系数模型对发动机和冷却液耦合温度场影响更大，表现为温度结果浮动更明显；采用Kocamustafaogullari气泡核点密度模型时3个火力面温度值相差不大，第2缸的预测结果十分接近试验值，但整体误差比基准模型大；采用Tomiyama的界面换热系数模型的仿真结果大于试验值。

3.3.3 非曳力系数模型比较

考虑Moraga的升力系数模型、Antal的壁面润滑力模型等非曳力的相间作用力，在基准模型基础上进行发动机过冷沸腾模拟，结果如图7所示。对比图7a与图4a、图7b与图6c可发现，模拟结果的温度差变化很小，这说明是否考虑除曳力之外的相间作用力，对高热流的发动机及冷却通道的模拟准确性影响不明显。

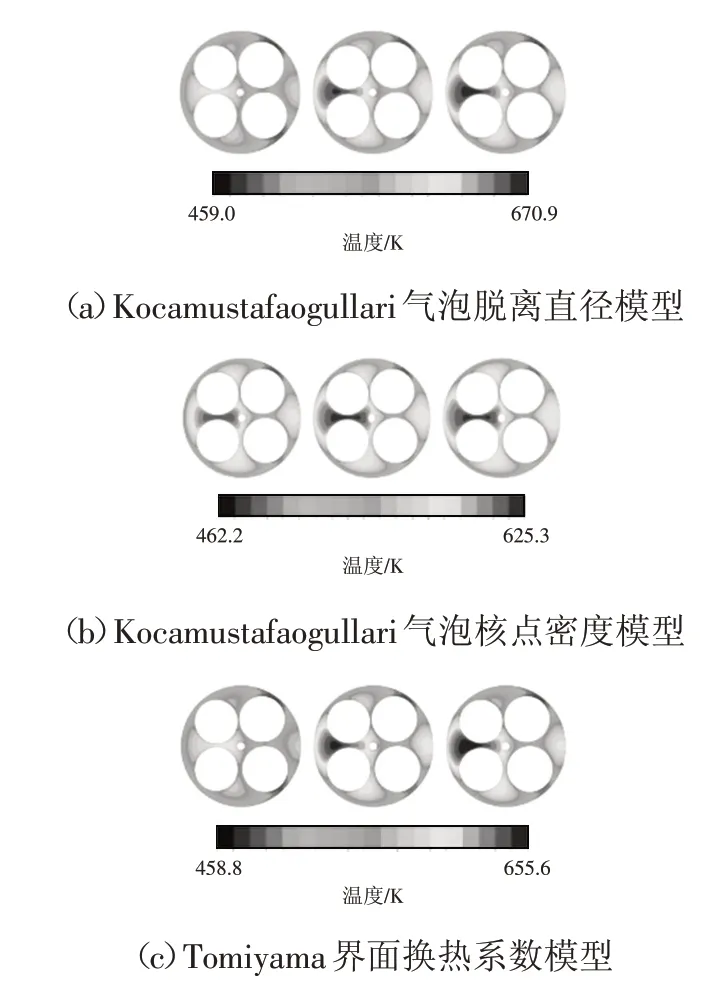
图6 采用不同换热模型的发动机火力面温度仿真结果

图7 考虑非曳力的相间作用力的仿真结果

Mixture模型的计算结果如图8所示，使用该模型的仿真结果与试验值相比偏高，相对误差明显大于使用Eulerian模型得到的仿真结果，说明该模型的仿真精确度较低。

图8 Mixture模型仿真结果

综上所述，在进行发动机冷却液过冷沸腾仿真时，采用Tolubinsky的气泡脱离直径模型、Cole的气泡脱离频率模型、Lemmer的气泡核点密度模型、Ranz-Marshall的两相间换热系数模型以及Schiller and Naumann曳力系数模型得到的仿真结果与试验测试结果最接近，使用上述子模型对发动机冷却液过冷沸腾进行仿真既可以节约计算成本，又能够保证仿真的准确性。

4 冷却通道结构研究

4.1 交界面温度

方案2中冷却液入口条件与原始条件相同，即入口温度为363 K，入口流量为15.1 m3/h。方案3中缸体的入口条件与原始条件相同，但缸盖冷却液入口条件有所变化，每个入口的冷却液流量为原流量的1/5，保持总流量不变。3种结构冷却通道的固液交界面温度如图9所示。

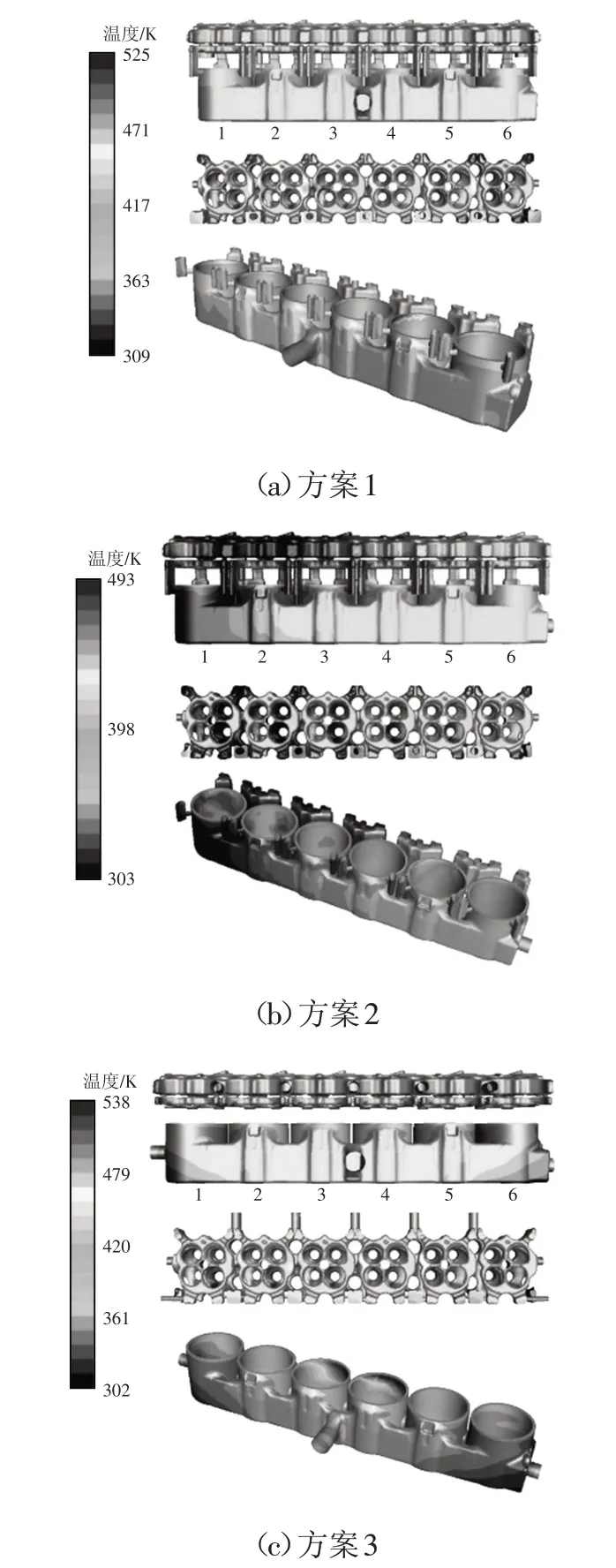
图9 不同冷却通道结构的发动机固液交界面温度

由图9可以看出，在方案1和方案3中，固液交界面或冷却液表面温度主要受冷却液温度影响，最小值为363 K，极少部分区域温度较低。方案2中出现大面积低温区域，该区域交界面温度与缸体外表面温度接近，为300 K左右；其余部分温度与冷却液温度（363 K）相同。

3种方案温度较高区域均出现在缸盖冷却通道近火力面处，以及缸体冷却通道近燃烧室区域上部边缘。方案1的最高温度出现在第5缸的缸体冷却通道近燃烧室区域上部边缘，为525 K，缸体冷却通道内侧表面平均温度约为430 K。缸盖冷却通道的最高温度接近500 K，位于第4缸、第5缸缸盖，内侧平均温度约为420 K，部分位置达到460 K。上述区域温度都达到了冷却液的沸点，而冷却通道外侧表面温度又低于冷却液沸点，说明冷却液在发动机冷却通道内发生过冷沸腾现象。方案2采用一侧入口流动的方式，冷却液主要由一侧流向另一侧，在流量相同的情况下，方案2大部分区域流速大于方案1，因此冷却液与缸体缸盖的交界面温度低于方案1。方案3与方案1缸盖冷却通道流量相同，但温度分布更均匀，在第3和第4缸体冷却通道内出现高温区，温度向两侧逐缸递减。

4.2 冷却液流速

3种方案的流速分布如图10所示，方案1和方案2呈现与之前分析一致的冷却液流速差别。由图10a可知，在缸盖冷却通道内冷却液流动减弱区域（第5缸）与图9中高温交界面所在区域一致，均在同一缸；由图10b可知，冷却液流动减弱区域与图9中缸体交界面高温区域相同，但在同一缸的缸盖区域没有受到明显影响而产生高温；由图10c可知，缸盖内冷却液流动更加均匀，这与交界面温度分布一致，但分离后的缸体中间位置的冷却通道内冷却液流动效果较差，其中高温区域即由此引起。

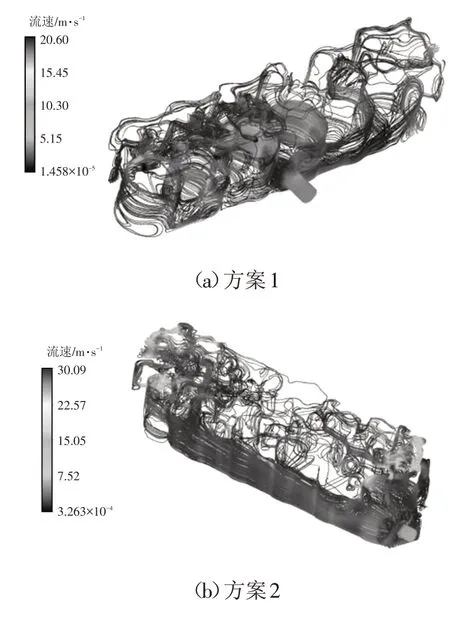
图10 不同冷却通道结构的发动机冷却液流速

3种方案中，冷却液最大流速均在出口位置，其中方案3由于增加了2个小出口，冷却液的流速减小。分离式的冷却通道减少了上、下冷却通道的连通，需要通过增加冷却液出、入口使冷却液均匀分布，如方案3缸盖冷却通道，否则会使流动出现“死区”，如方案3缸体冷却通道。串联模式的发动机冷却通道虽然有较多的连接口，但也产生冷却液流动减弱区，如图10中方案1的缸盖冷却通道和方案2的缸体冷却通道。方案1采用对称的3缸串联模式，方案2采用6缸串联模式。

4.3 冷却液气相分布

过冷沸腾产生的气体分布如图11所示，方案1和方案3中都有较大面积的气相覆盖区产生，而方案2气相覆盖区面积很小。气相覆盖区均产生在高热流量（燃烧室附近）区域，外侧气相分布为0，这与过冷沸腾现象吻合。方案1和方案3分别在第5缸缸盖和第3缸、第4缸缸体产生比其他缸更多气相，与流速减弱区域出现的位置相同。方案2中由于冷却液流速较高，气相分布区产生较少。

图11 不同冷却通道结构的发动机冷却液气相分布

相对于方案3，方案1的缸盖冷却通道气相分布更广，这也是由冷却液流动不均匀引起的。方案1的缸体冷却通道由中间向两侧气相分布逐渐增加，而方案3则是在中间2缸集中更多的气相。方案1由于冷却液温度逐渐上升，使冷却液到达饱和温度所需要的热量降低，更多富余的热量转化为液体汽化所需的潜热；方案3由于流动缓慢进而导致冷却液加热时间过长。

5 结束语

本文针对发动机冷却通道过冷沸腾多相流模拟中采用模型的复杂性和多样性问题，通过一系列仿真模拟和试验验证表明：发动机冷却液过冷沸腾多相流模拟中，采用Eulerian模型比Mixture模型模拟结果更加准确；在高入口温度和高热流量的条件下，在Eulerian模型中采用Tolubinsky的气泡脱离直径模型、Cole的气泡脱离频率模型、Lemmer的气泡核点密度模型、Ranz-Marshall的两相间换热系数模型、Schiller and Naumann曳力系数模型，可以得到准确的模拟结果。通过模拟分析可知，分离式冷却通道结构设计可以使温度分布更均匀，但需要更多的出入口设计，连体式的冷却通道结构需要注重上、下冷却通道的串联和出、入口位置的选择。