复杂航天器结构火工冲击环境预示方法研究

赵宏达，丁继锋，郝志伟，刘 伟，孙 毅，刘一志

(1. 哈尔滨工业大学航天学院，哈尔滨 150001；2. 北京空间飞行器总体设计部，北京 100094)

0 引 言

在航天工程中，火工分离装置被广泛用于实现航天器与运载之间的连接-分离功能[1]。常见的火工分离装置有爆炸螺栓、火工分离螺母、导爆索、膨胀管等。当航天器与运载分离时，这些分离装置内部火工品能量高速释放，在航天器结构上产生具有瞬态、高频和高量级特点的冲击响应，称为火工冲击环境。这种冲击环境往往会使航天器上的仪器设备激起固有频率响应，使产品性能和结构受到不同程度的损伤或失效[2](如晶振断裂、焊点脱落、陶瓷破裂、继电器抖动等)，甚至可能导致整个航天任务的失败。因此，开展航天器结构的冲击环境预示方法研究对航天器初期结构设计及布局优化具有重要的指导意义。

航天器冲击响应预示方法有试验外推法、理论计算方法、有限元法和虚拟模态综合法等。美国NASA和法国国家空间中心(CNES)较早采用试验外推法对卫星结构的冲击响应进行预示[3-4]。在大量试验数据的基础上，NASA总结出了数据外推公式并写入了相关标准NASA-STD-7003A。试验外推法是一种经验公式方法，具有操作简单和使用方便等优点，但该方法严重依赖于丰富的数据库和模型的相似性。因此其使用范围目前受到一定限制。在理论计算方面，文献[5-6]等对冲击载荷作用下的响应计算模型进行了研究，推导了相应的计算公式。理论模型计算方法精度较高，但过程较为复杂仅适用于简单的结构模型。在有限元方法方面，法国国家宇航局(CNES)以SPOT5卫星为对象应用显式有限元进行了响应计算[7]。文献[8]对超热电子与质子仪(STEP)进行了建模与冲击仿真计算，并以有限元方法所得结果作为参照对其它预示方法的准确性进行了评价。由于火工冲击的高频特性，有限元方法在进行冲击响应计算时网格须划分足够细密(每个波长内至少包含6个单元)才能获得较为准确的结果。虚拟模态综合法由Dalton和Chambers[9]于1995年首次提出。他们将现有的计算稳态频响函数(Frequency response function,FRF)包络的方法论拓展至瞬态响应计算，并开发了相应的计算程序MANTA。虚拟模态综合法自提出以来就受到广泛关注。目前该方法已集成于商业软件VA One中的Shock模块[10]，极大地促进了该方法在冲击响应计算方面的应用。王军评等[11]采用虚拟模态综合法对切割索产生的火工冲击环境进行了响应计算。曹乃亮等[12]采用SEA+VMSS方法对空间光学遥感器冲击响应进行计算，获得了不同子系统冲击响应谱，并通过与试验数据对比，验证了方法的可靠性。韩国科学技术院(KAIST)的Lee等[13]和Kafle等[14]分别采用VA One中Shock模块对卫星结构的冲击响应进行了计算与分析。

对于复杂航天器结构，其各子系统动力学特性存在显著差异。在具有宽频、瞬态特点的火工冲击载荷激励下，一些刚度较大、模态稀疏的主承力结构(如连接接头、连接梁等)表现出低频响应特性，而对于模态密度较高的子系统(如舱板，太阳翼等)则表现出高频模态随机特性[15]。有限元法(Finite element method,FEM)和统计能量方法(Statistical energy analysis,SEA)分别是处理低频问题和高频振动问题的有效手段。建立单一的复杂航天器结构的有限元模型或统计能量模型均无法获得令人满意的结果。因此，采用FE-SEA混合建模是一种行之有效的方法。文献[16]对FE-SEA混合线连接的基本理论进行了详细推导，并深入研究了混合线连接建模理论。文献[17-18]等也对FE-SEA混合方法开展了相关研究，取得了较好的分析结果。

本文以某型复杂卫星结构为研究对象，首先进行模态子系统划分，建立其FE-SEA混合模型并进行求解。然后采用虚拟模态综合法对复杂卫星结构的推进舱冲击响应进行计算。最后开展整星分离冲击试验并将试验结果作为参照，对计算结果的准确性和方法的可靠性进行了分析验证。

1 基于加速度频响函数的虚拟模态综合法

本章重点推导解决航天器冲击环境瞬态特性的虚拟模态综合法的理论，获得基于加速度频响函数包络曲线的冲击响应计算程序。

对于离散的多自由度系统，其在外载荷作用下的控制方程可写为：

(1)

式中：M，C和K分别为系统的质量矩阵，阻尼矩阵和刚度矩阵，q(t)为位移向量，F(t)为外力矢量。

将式(1)进行模态解耦，可得其解耦后的表达式为：

(2)

当方程(1)解耦后，系统在每一自由度的动力学方程可写为：

(3)

其中，s=1,…,ns。方程(3)两边同时作傅里叶变换，并且假设零初始条件，可以转化为：

(4)

系统的位移频响函数可以表达为：

(5)

在稳态条件下，加速度响应在频域与位移响应有如下关系：

(6)

因此，加速度频响函数可由式(5)和式(6)联合得出，其表达式为：

(7)

在小阻尼假设条件下，系统所有模态具有相同的相位，即使在非共振条件下也满足该结论[10]。因此，加速度频响函数的幅值简单等于每一阶模态响应的幅值的求和并近似表示为如下关系式：

(8)

为表示方便，将式(8)重新写为如下两个向量相乘的形式，即：

|H′lj(iΩ)|=ΛTΦlj

(9)

其中，

Φlj=[φl1φj1,φl2φj2,…,φlnsφjns]T

式中：Ω为按一定规则选定的离散频率，Φlj为虚拟模态向量。

通过选择一系列的离散频率Ω，在相应的离散频率处的频响函数值矩阵为H′lj(iΩ)。式(9)可以重新写为：

|H′lj(iΩ)|=ΛTΦlj

(10)

式中：Λ=[Λ(Ω1),Λ(Ω2),…,Λ(Ωk)]。

设置在每一频带内离散频率数k与在该频率带宽内的虚拟模态数相同，则可由下式合成虚拟模态向量：

Φlj=(ΛT)-1|H′lj(iΩ)|

(11)

其中，加速度频响函数包络可以基于稳态的方法获得，该部分将在第2节详细讨论。共振频率可由频率带宽和相应的模态密度分析得到。

当虚拟模态向量合成后，加速度在频域的响应可由下式计算：

(12)

得到加速度在频域响应结果后，可通过对频域结果进行傅里叶逆变换(IFFT)得到加速在时域的响应结果。加速度冲击响应谱也可由加速度时域响应通过相应的计算程序获得。

2 复杂卫星结构火工冲击响应预示

2.1 整星FE-SEA混合建模

航天器火工冲击环境预示一般处于结构初样设计阶段，此时尚不具备对其结构开展试验以获得频响曲线及模态数曲线作为预示输入的条件。此外，考虑到试验所需较大的人力物力及时间成本，工程中更为一般的方法是采用数值方法进行实现。复杂航天器各子系统动力学特性存在较大差异。一方面，其主承力结构一般为框架结构，通常由卫星接头、连接接头以及连接梁等组成。这些主承力结构多为高强铝合金或碳纤维杆，往往具有较高的刚度，模态较为稀疏。传统的有限元方法(FE)能够准确地对其进行响应计算。另一方面，复杂航天器中的舱板和隔板等板壳结构模态密度较高，在高频火工冲击载荷作用下则表现出高频模态随机特性。统计能量方法(SEA)是解决高频随机响应的有效方法，适用于对舱板及隔板等结构响应计算。

综上所述，就复杂卫星结构而言，建立单一的FE模型或SEA模型均是不合理的。因此本文对复杂卫星结构开展FE-SEA混合建模。

图1为某型复杂卫星结构的FE-SEA混合模型。模型中卫星接头、连接接头及连接杆等刚度较大的主承力结构建立为FE模型，卫星舱板，隔板等模态密度较大的板壳结构建立为SEA模型。FE子系统与SEA子系统之间通过混合线连接或混合点连接(分别如图1(b)～图1(d)中标注“1”和“3”所示)实现其相互作用。复杂卫星结构FE-SEA混合模型中共包含39个FE子系统，18个SEA子系统以及4个混合线连接和410个混合点连接。此外模型中还包含若干SEA子系统之间的线连接以及FE子系统之间的点连接(共节点)，分别如图1(b)～图1(d)中标注“2”和“4”所示。

图1 整星FE-SEA混合模型及局部图Fig.1 FE-SEA hybrid model of the complex satellite and its local view

复杂卫星FE-SEA混合模型中四个卫星接头分别施加单位正弦激励力载荷，并进行响应求解。推进舱底板和+X板的稳态加速度响应曲线如图2所示。由于激励力为单位载荷，故卫星舱板的响应曲线即为频响曲线。图3为推进舱底板和+X板的模态数曲线。从图2和图3可以看出，推进舱底板和+X侧板具有相似的频响曲线以及相近的模态数曲线。这是由于推进舱底板和侧板具有相同的材料参数(铝蜂窝板)和相似的几何尺寸(底板：1000 mm×1000 mm×25.6 mm；+X侧板：1000 mm×800 mm×25.6 mm)及约束条件。此外，推进舱底板靠近四个激励力，且响应主方向与激励力方向一致，因此推进舱底板响应明显高于+X侧板，这与能量传递规律吻合。

图2 推进舱底板和+X板的频响曲线Fig.2 Steady FRF curves for the bottom panel and +Xpanel of propulsion cabin

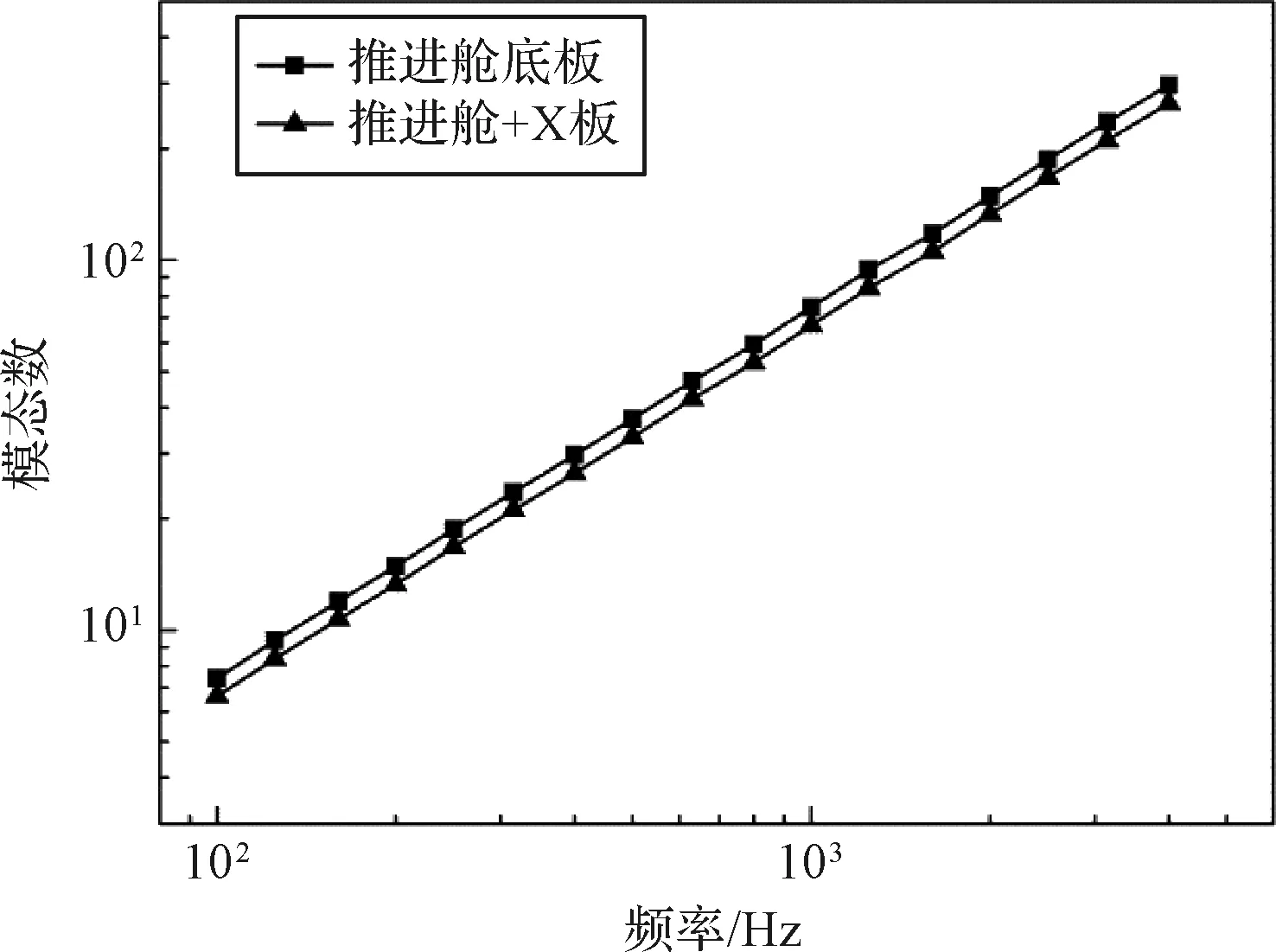
图3 推进舱底板和+X板的模态数曲线Fig.3 Mode number curves for the bottom panel and +Xpanel of propulsion cabin

2.2 星箭界面冲击力函数

由式(12)可知，在获得复杂卫星结构频响包络曲线及模态数曲线后，仍需冲击力函数作为外力输入。星箭分离火工冲击源的冲击力函数等效是工程中的难题。目前，星箭界面冲击力函数的获取方法主要包括显式有限元法和反推法[19]。显式有限元法是建立火工冲击源的有限元模型并进行数值求解，利用计算程序提取星箭界面力函数。该方法的准确性依赖于星箭火工分离近场结构模型的精细程度，有时甚至需要开展近场火工冲击试验对近场有限元模型进行修正。反推法将星箭界面的冲击力函数假设为一种固定的波形，如三角波、梯形波、半正弦波等，波形参数通过多次加载计算并与试验结果进行对比得到。使用这种方法需要反复进行不同参数、不同波形的试算，有时多次试算仍难以得到准确的力函数。

文献[20]采用显式有限元法计算获得了星箭界面冲击力函数，并指出界面力在竖向分量远大于两个水平方向的分量。因此，本文采用上述文献中竖向力函数等效星箭分离界面火工冲击作用。冲击力函数曲线如图4所示。

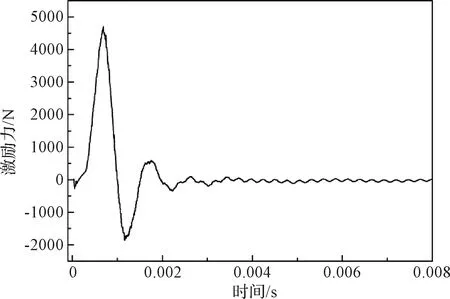
图4 冲击力函数Fig.4 Function curve of shock force

2.3 冲击响应预示

当频响函数曲线及模态数曲线已知后，由第1节虚拟模态综合法理论程序求解模态系数向量，从而合成近似真实的频响函数。图5中三条曲线分别为推进舱底板单位力加载频响曲线、合成的近似真实的频响函数曲线以及星箭界面力函数频率对应的频响曲线。从图5可以看出，第2.1节混合模型计算的频响曲线近似为合成频响函数曲线的上限，且合成频响函数曲线将界面力函数对应频响函数包络于其上限和下限范围内。

图5 推进舱底板的三条频响函数曲线Fig.5 Three FRF curves for the bottom panel of thepropulsion cabin

当频响函数及界面力函数已知时，由式(12)可以计算得到复杂卫星结构的火工冲击加速度频域响应，并进一步通过傅里叶逆变换得到加速度时域结果。推进舱底板和+X侧板的加速度时域响应曲线如图6所示。由图6可知，推进舱两块舱板的加速度响应在初始时刻出现较大峰值，且随着时间推移逐渐衰减，至20 ms时响应近似完全衰减。图中推进舱底板的响应峰值明显大于+X侧板的响应，这是由于推进舱底板靠近四个火工冲击源，且其响应主方向与激励力方向相同，故其单位力加载频响曲线高于+X侧板造成的。图6中计算结果与第2.1节分析相一致。

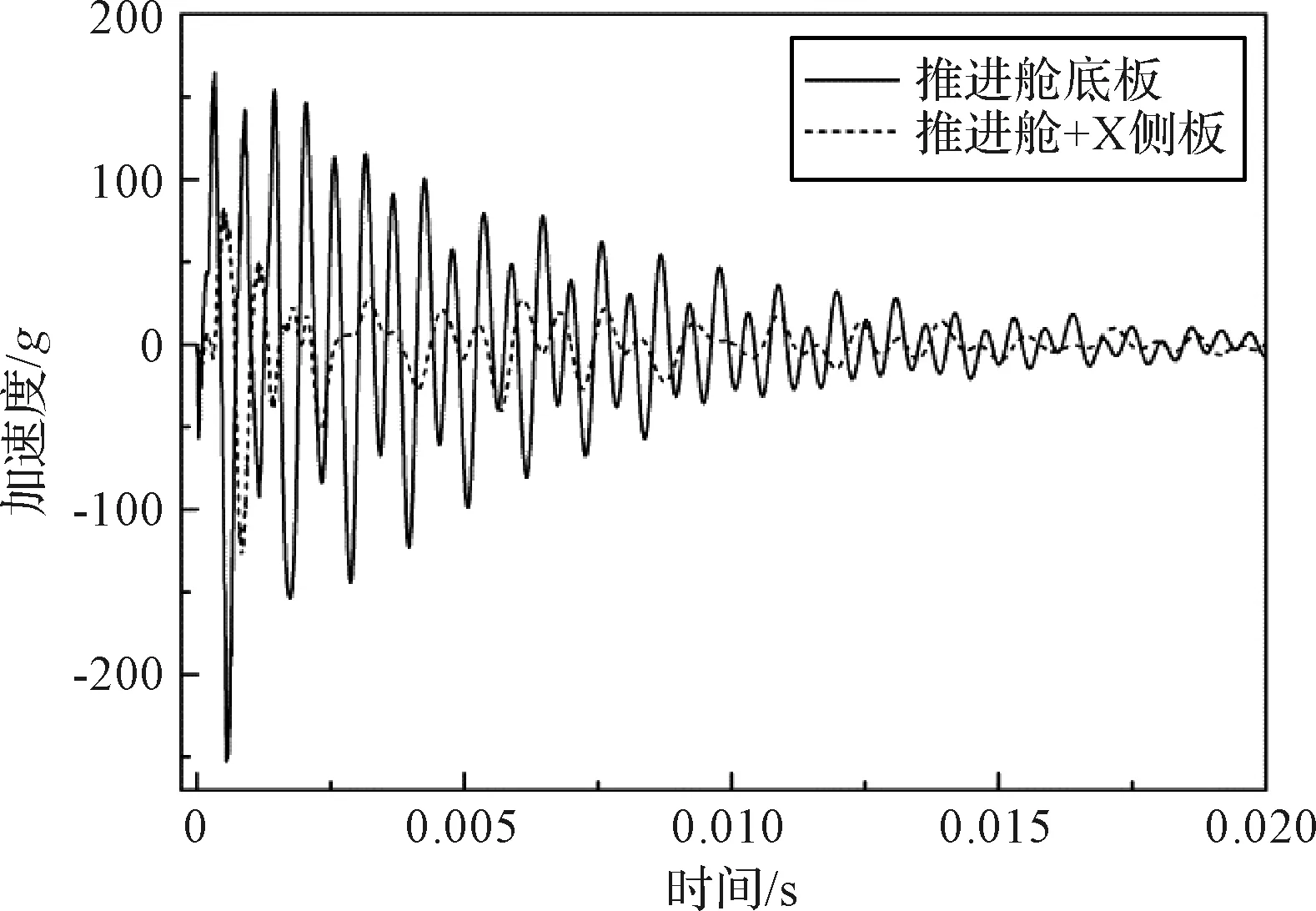
图6 推进舱底板和+X侧板的加速度响应Fig.6 Acceleration histories for the bottom panel and +Xpanel of the propulsion cabin

航天器火工冲击响应在时域多表现为复杂的振荡波形，不利于比较分析。在工程中，常以冲击响应谱(Shock response spectrum, SRS)作为考核冲击强弱的指标。所谓的冲击响应谱就是将时域响应信号加载至一系列不同固有频率的单自由度系统上，然后以固有频率为横坐标，对应该固有频率下单自由度系统响应最大值为纵坐标所作的一条频域曲线[21]。文献[22]对冲击响应谱的计算方法进行了详细介绍。将图6中推进舱底板和+X侧板加速度时域响应进行冲击响应谱变换，得到两者冲击响应谱曲线如图7所示。由图7可知，推进舱底板和+X侧板的拐点频率约为1700 Hz。除在200 Hz以下两条曲线的值相近外，在大部分频率范围内推进舱+X侧板的SRS谱值均小于推进舱底板。在拐点频率处推进舱底板的峰值约为+X侧板峰值的3倍，表明推进舱底板的火工冲击环境更为严酷，应尽量避免布置精密设备，必要时在设备安装处进行隔冲设计。

图7 推进舱底板和+X侧板的冲击响应谱Fig.7 SRS curves for the bottom panel and +X panel ofthe propulsion cabin

3 整星分离冲击试验验证

3.1 整星分离冲击试验

整星火工分离冲击试验示意图如图8所示。试验前将整个卫星结构通过柔性绳悬挂于试验架上。卫星接头与运载接头通过四个火工分离螺栓连接，并通过向螺栓施加标准预紧力使得星箭界面产生可靠的连接刚度。试验中使用的火工分离螺栓为F12A改进型。分离火工品使用半套状态改进型非电传爆装置FSJ2-23B。星箭分离弹簧采用4个分离弹簧YA0-10。推进舱底板和侧板均布置有加速度传感器。试验时，同步引爆四个火工分离螺栓，实现卫星与运载分离，并在卫星结构上产生火工分离冲击环境。最终通过加速度传感器获得其响应数据，为星箭分离火工冲击响应预示精度分析提供试验数据支撑。

图8 星箭分离冲击试验示意图Fig.8 Schematic diagram of the separation experiment ofthe complex satellite

3.2 结果与讨论

复杂卫星推进舱底板和+X侧板的计算冲击加速度响应与整星分离冲击试验结果对比分别如图9(a)、图9(b)所示。图中计算结果与试验测得响应曲线具有相似的振荡波形，且均在20 ms内近似完全衰减。在冲击响应前期，两块舱板的计算加速度响应小于试验测试结果，这是由于整星FE-SEA混合模型简化以及界面力函数简化等引入的误差造成的。整体而言，复杂卫星推进舱两块舱板的预示结果与试验结果较为接近，表明预示结果具有一定的可靠性。

图9(c)、图9(d)分别为推进舱底板和+X侧板计算结果和试验结果的冲击响应谱对比。以试验测试结果的冲击响应谱曲线为“标尺”，作其±6 dB范围。由图9可知，推进舱两块舱板计算结果的冲击响应谱与试验结果冲击响应谱具有相似的谱形，且幅值接近。在整个冲击响应谱频域范围内，舱板计算结果的冲击响应谱曲线基本包络在试验结果的±6 dB范围内，表明预示结果具有较高的精度，满足相应的工程要求。

图9 推进舱两块舱板计算和试验结果对比Fig.9 Comparison of calculation and experiment results of the two panels of propulsion cabin

上述分析表明复杂卫星结构的冲击响应计算结果和试验结果在时域和冲击响应谱频域均具有良好的一致性，联合整星FE-SEA混合建模和虚拟模态综合法能够对复杂卫星推进舱底板和+X侧板的火工冲击环境给出较为准确的预示结果。

4 结 论

本文以某型复杂卫星结构为例，建立其FE-SEA混合模型并进行响应计算，解决了复杂卫星结构在宽频火工冲击激励下各子系统动力学响应特性差异较大难以预示的问题。采用虚拟模态综合法对复杂卫星结构推进舱进行了冲击响应预示，并与试验结果进行对比，验证了预示结果的准确性和方法的可靠性。本文得到如下结论：

1)针对复杂航天器结构建立FE-SEA混合模型进行求解能够克服火工冲击宽频激励下各子系统呈现出显著动力学差异的问题。

2)基于加速度频响曲线的改进虚拟模态综合法能够直接获得结构加速度响应，是解决瞬态响应问题的可靠手段。

3)联合FE-SEA混合建模技术与虚拟模态综合法能够对复杂航天器结构的火工冲击环境进行较为准确的预示。

本文提出的对复杂卫星结构采用FE-SEA混合建模并利用虚拟模态综合法进行火工冲击响应预示的研究方法和结论对今后的相关工作的开展具有一定参考价值。