钻井液设计专家系统规则库的检测算法

李 建，习文风

西南石油大学 计算机科学学院，成都610500

1 引言

钻井液设计专家系统结合来自于领域专家的经验规则库，应用基于规则的推理技术，通过钻井地层的地质结构、地层特征和油气井信息等数据来设计满足条件的钻井液体系和配方，以达到快速优质钻井的目的，同时也能有效地保存经验数据和避免重复性工作[1-2]。

但是，随着规则的不断增加，规则库日益繁杂，对规则库的维护已经成为制约专家系统效率的重要因素。一般而言，对规则库的维护主要包括从属、冗余、环路和冲突四方面[3]。

针对规则库的维护问题，文献[4]研究了规则库添加新的规则后对冗余的判别、处理以及校验的实现方法，但并未对环路和冲突等问题进行研究；文献[5]讨论了规则库的一致性检测，并对冲突消解进行了研究，但并未提及对冗余和环路等问题的检测；文献[6]结合有向超图和生成树，提出了一种能够去除从属和冗余的算法，但没有研究环路和冲突等问题；文献[7]研究了粗糙集理论，通过对决策表进行属性约简来去除冗余规则，并对剩余规则进行排序，但同样没有提及对环路和冲突等问题的处理；文献[8]提出了一种基于知识约简的Petri网模型简化方法，利用知识约简中的属性约简方法，去除了Petri网对应的产生式规则的冗余规则和冗余条件；文献[9]提出了一种基于Petri网的冗余检测算法；文献[10]在有向超图的基础上提出了一种规则库的合并算法，并且研究了如何检测冗余、环路和冲突，但算法所构建的邻接矩阵规模太大，导致效率较低。

总的来说，目前应用于规则库维护的方法主要有表格法、基于Petri网的方法、基于图的方法和基于代数插值的方法等[11-14]。其中，有向图因其便于表示规则之间的关系而成为研究规则库维护的重要工具。又因为钻井液设计专家系统中的规则很多都是多对一的关系，所以本文引入有向超图来表示规则[15-18]。

为了避免不能将规则库中问题全部检测而影响推理效率和推理准确性的不利后果，本文提出了一种能够检测从属、冗余、环路和冲突等全部问题的算法，同时降低了算法中矩阵的规模，保证了运算效率。

本文首先介绍了如何用有向超图来表示规则库中的规则以及如何构建对应的邻接矩阵，然后讨论了可达矩阵的概念和计算，并在此基础上给出了规则库的检测算法，最后通过实验对算法的可行性和有效性加以验证。

2 钻井液设计专家系统规则库

2.1 钻井液的功用及体系

在钻井中用作洗井的流体被称为钻井流体，因为钻井流体多属于液体，气体型钻井液很少被使用，所以简称为“钻井液”。

钻井时，钻井液除了需要保护所钻油气储层外，还担负着以下任务：润滑、冷却钻具、热稳定性、岩层稳定性、平衡压差、较强的清井及携岩能力等。这些都是由于地下钻井油气层的差异性和复杂情况以及不同井型对钻井液设计提出的要求。

钻井液体系种类随着具体要求和钻井液技术的进步而逐渐增多。目前，国内外分类钻井液的方法有很多种，根据体系组成特点和流体介质的不同，可以把钻井液分为油基、合成基、水基、气体型四种类型，每种类型又包含多种钻井液，如图1所示。

2.2 规则库

规则库是钻井液设计专家系统的核心部分，专家系统的所有操作都是围绕规则库进行的。在对规则库进行增删改等操作时，若没有考虑到规则知识结构的应有变化，容易导致规则库出现问题，从而不能推理出正确的结果。

一般情况下规则库中的问题主要包括：

从属：存在能产生相同规则，但条件却是包含关系的两条规则。

图1 钻井液体系分类

冗余：存在两条等价的规则。

环路：一组规则互相推出，会使推理进入死循环。

冲突：两条规则在相同条件下产生相互矛盾的结果。

由上述可知，在对规则库进行增删改等操作后有必要对其进行检测，以保证它能正确有效地发挥作用。

3 有向超图及其邻接矩阵

3.1 规则的表达形式

一个规则的一般形式可以表达为：

IF x1∧x2∧…∧xnTHEN xn+1

可简写：

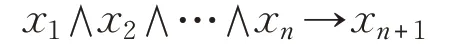
其中，规则的左部称为规则的条件部分，或叫作规则前件；右部称为规则的结论部分，或叫作规则后件。上述规则的含义为：如果条件部分x1,x2,…,xn都得到满足，则执行结论部分xn+1。

而如果规则的条件部分只包含一个选择子，则该规则称为简单规则，否则称为复合规则。例如，规则R：

IF泥页岩成分>50%∧含砂量>10%THEN钻井液类型为盐水钻井液

则规则R为复合规则，将R的前提记为ante(R)，结论记为cons(R)，其中前者为由两个选择子组成的集合。

3.2 有向超图与邻接矩阵

有向超图是有向图的推广，它是在无向超图中每条超边的基础上添加方向所得。

定义1（有向超图）有向超图是由有限非空顶点集V和有向超边集E组成的有序对H=(V,E)。有向超边e∈E是有序对(T(e),H(e))，其中T(e)为有向超边e的尾点集，H(e)为有向超边e的头点集，T(e)与H(e)均为V的非空子集，且T(e)∩H(e)=∅。

与有向图不同，在有向超图中，超边e所连接的可以是由多个顶点组成的点集，这一性质适用于表示含有复合规则的规则库。

利用有向超图可以将规则库（下述规则为示例所用，其选择子x无实际意义）表示为如图2所示形式。

图2 规则库的有向超图表示

规则1 x1→x2；

规则2 x2→x4；

规则3 x3∧x4→x5，记为R1；

规则4 x3∧x6→¬x2，记为R2。

假设规则库中有n个选择子（其中¬x选择子有d个），分别记为x1,x2,¬x2,…,xn-d，并假设规则库中有m条复合规则，分别记为R1,R2,…,Rm。

定义2（邻接矩阵An×n）如果规则库中不存在前提包含xi结论为xj的规则，记Ai,j=0；如果规则库中包含简单规则xi→xj，记Ai,j=1，而若包含简单规则xi→¬xj,则Ai,j+1=-1,若对应的¬xi→xj,则Ai+1,j=-1,而¬xi→¬xj，则将规则转换为其逆否命题xj→xi；如果规则库中存在复合规则Rm，其前提包含xi，结论为xj，则Ai,j表示为二元组(xi,Rm)，而若结论为¬xj，则Ai,j表示为二元组-(xi,Rm)。

根据邻接矩阵的定义可得图2有向超图的邻接矩阵为：

邻接矩阵可以通过扫描规则库得到。显然，在扫描过程中，如果元素|Ai,j|=1，则所有前提包含xi且结论为xj的复合规则均为从属规则，从规则库中删除；如果元素Ai,j=±(xi,Rm)，则所有从属于Rm的复合规则均从规则库中删除。

3.3 有向超图的路径长度

定义3（路径长度）路径长度指该路径从起点到终点所经过的最长路径。即从xi到xj的某条路径长度为k的条件是：对该路径的最后一条规则R（显然其结论为xj），从xi到ante(R)中至少一个元素的路径长度为k-1。

如图3所示，从x1到x5存在两条路径：（1）x1→x2,x2→x4,x3∧x4→x5；（2）x1→x3,x3∧x4→x5。在路径（1）中，由规则的传导性可知x1到x4的路径长度为2，而规则x3∧x4→x5的ante(R)中蕴含了规则x2→x4的cons(R)，因此路径（1）中从x1到x5的路径长度为3，同理可得路径（2）中从x1到x5的路径长度为2，取最长路径得图3中从x1到x5的路径长度为3。

图3 有向超图的路径长度

4 有向超图的可达矩阵

4.1 可达矩阵的定义

有向超图的可达矩阵有两种：

若计算完Ek仍未检测到冗余、环路、冲突，则Ek内元素绝对值均为0或1。为了便于后续的计算，将当前总可达矩阵Ek中非零元素的路径长度存入矩阵Fn×n。

由定义3有向超图的路径长度可得Fn×n的定义为：

由定义可知，如果当前Dk中至少有一个元素绝对值为1，则Fn×n中对应位置的元素为k。因此，将Fn×n初值赋为，当计算完Dk(k=2,3,…)时，Fn×n更新为：

4.2 计算总可达矩阵E k+1

由邻接矩阵的定义可知，将A中绝对值不为1的元素赋值为0，即可得到一步可达矩阵D1n×n和一步总可达矩阵E1n×n。

假设Dk和Ek都已求得，欲求Ek+1，需要先计算Dk+1。那么：

可得：

规定（矩阵中所有元素在计算过程中取绝对值参与计算，得出结果后再保持与同号）：若=0或Al,j=0,l=1,2,…,n，则若=1⋅(xp,R′)，且记R′为xp∧xq→xj，则：

5 规则库检测算法

本文提出了一种针对规则库中从属、冗余、环路和冲突的检测算法，算法的具体步骤如下：

（1）整理规则库，根据定义1所定义的有向超图来表示规则库中的规则。

（2）根据定义2构建出该有向超图的邻接矩阵An×n。

（3）预处理邻接矩阵，判定并删除An×n中的从属规则：如果元素1，则所有前提包含xi且结论为xj的复合规则均为从属规则，从规则库中删除；如果元素Ai,j=±(xi,Rm)，则所有从属于Rm的复合规则均从规则库中删除。

（4）将An×n中绝对值不为1的元素赋值为0得到一步可达矩阵和一步总可达矩阵，再将An×n中所有元素取绝对值得到路径长度矩阵Fn×n，同时判断：若||≥1，则规则库中存在环路；若||=1且=-1或者|=1且||=-1，则规则库中存在冲突。

算法流程图如图4所示。

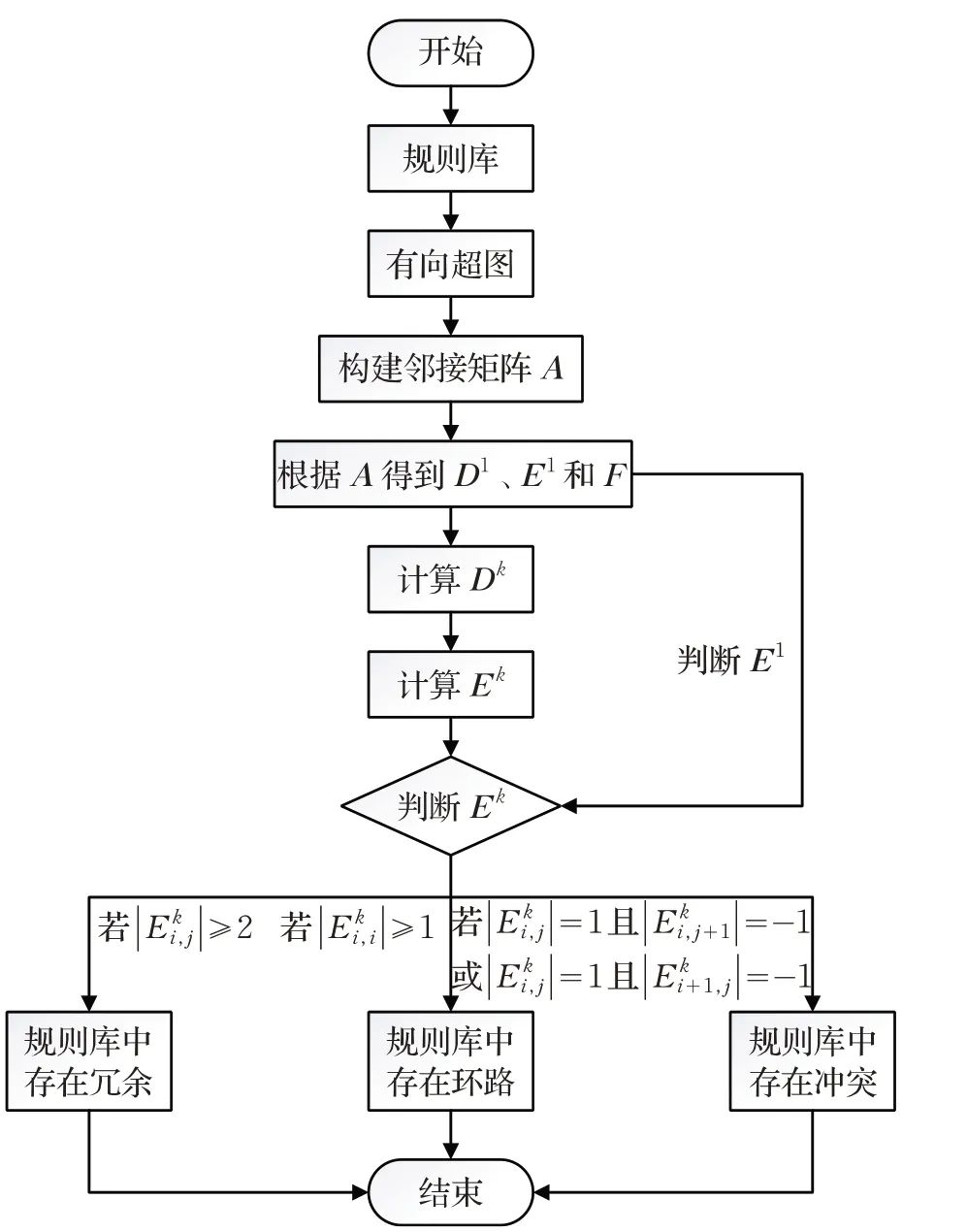
图4 算法流程图

该算法的复杂度与规则库的规模、选择子的数量以及路径长度有关。假设规则库中规则的数量为m，选择子的数量为n，路径长度最长为r。

计算邻接矩阵An×n需要扫描规则库，该步骤的复杂度为O(m)。由计算Dk+1=Dk⋅A，复杂度为O(n3)；计算复杂度为O(n2)；计算Fn×n+→Fn×n,复杂度为O(n2)；扫描，检测冗余、环路和冲突的复杂度为O(n2)。

最大循环次数为r，因此总的复杂度为O(m)+r(O(n3)+O(n2)+O(n2)+O(n2)),约等于O(m+rn3+3rn2)。

因为算法中的矩阵大多是稀疏矩阵，所以还可以利用零元素节省大量存储、运算和程序运行时间，从而进一步确保效率。

6 实验

6.1 实例验证

以下为钻井液设计专家系统规则库中的部分规则：

x1→x2；（若钻井液类型为水基，则对漏失类型为渗漏的地层有效）

x1→x3；（若钻井液类型为水基，则对漏失类型为完全漏失的地层有效）

x1→x6；（若钻井液类型为水基，则对漏失类型为严重完全漏失的地层有效）

x4→x6；（若采用剪切稠化堵漏剂，则对漏失类型为严重完全漏失的地层有效）

x4→¬x3；（若采用剪切稠化堵漏剂，则对漏失类型为完全漏失的地层无效）

x2∧x3→x4，记为R1；（若地层漏失类型为渗漏或者完全漏失，则应采用剪切稠化堵漏剂）

x4∧x5→x1，记为R2。（若采用剪切稠化堵漏剂，并且加入细粒桥堵剂，则其适用于水基类型钻井液）

将上述规则表示为图5所示的有向超图。

图5 案例所述规则的有向超图表示

将图5表示为邻接矩阵得：

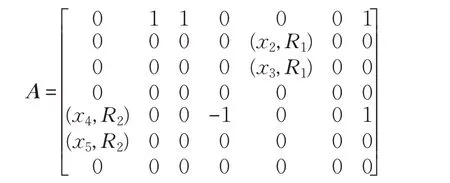
将A中绝对值不为1的元素赋值为0可得D1和E1，再将所有元素取绝对值得到F：

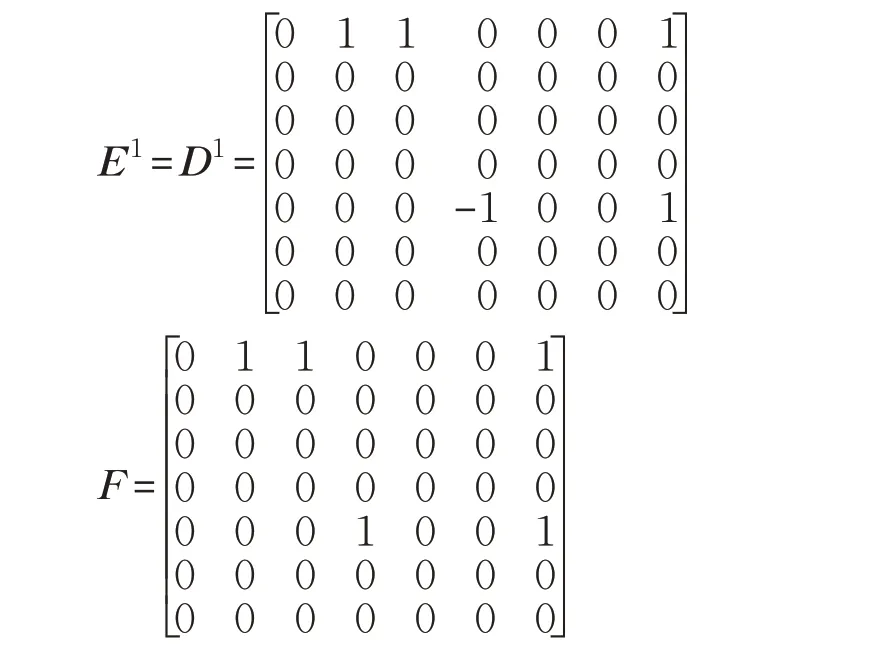
判断E1，未检测到冗余、环路或冲突，计算D2：

D2=D1⋅A

由式（2）：存在规则R1:x2∧x3→x4，由于F1,2=F1,3=1，可得D21,5=1。

判断E2，未检测到冗余、环路或冲突，计算D3：

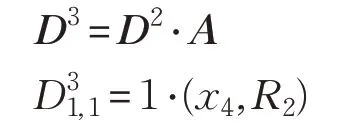
由式（1）：存在规则R2:x4∧x5→x1,由于F1,5=2≤2,可得D31,1=1。

根据第5章的检测算法判断E3：|=1≥1，检测到环路，即x1可达x1；E13,3=1且E13,4=-1，检测到冲突，即x1可达x3同时可达¬x3；E31,7=2≥1，检测到冗余，即x1通过两条路径可达x6。

可以看出，本算法能够有效地检测出规则库中存在的从属、冗余、环路和冲突等全部问题，且整个算法的计算过程较为简单快速。

6.2 对比分析

本算法能够有效地检测出规则库中的从属、冗余、环路和冲突等全部问题，相较于文献[4-9]中提出的算法，针对于其中的一种或几种，本算法能够将规则库中的问题更加全面地检测出来。

根据文献[10]中算法得到图5的邻接矩阵为：

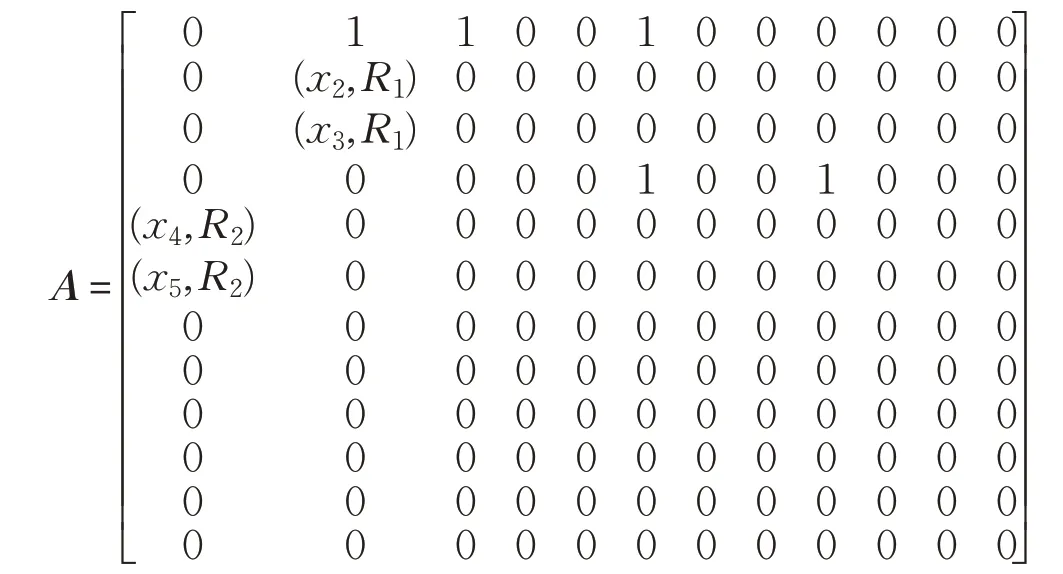
将A中绝对值不为1的元素赋值为0得到D1、E1和F：

对比本节实例验证部分可以看出，本算法构建的邻接矩阵规模大约减小了3/4，同时后续所有参与运算的矩阵规模都随之大大减小，使得运算效率获得了较大提升。

7 结论及展望

本算法结合有向超图和邻接矩阵来表示规则，通过计算可达矩阵和总可达矩阵来检测规则库中存在的问题。实验表明，本文提出的算法能够准确地检测出规则库中存在的从属、冗余、环路和冲突等全部问题，而且算法构建的邻接矩阵规模较小，参与运算的矩阵又大多是稀疏矩阵，因此计算过程较为简单快速，从而确保了效率。而当规则结论部分为由若干选择子组成的集合时，对规则库从属、冗余、环路和冲突的检测有待进一步研究。

另外，当规则的数量很大时，参与计算的矩阵规模也会变得很大，算法的效率可能会随之下降，这时可以先对规则进行分类处理，为其设计一个分类算法，本文的下一步工作将围绕着这个问题展开。