液压式天然气压缩机气阀设计及优化

(中石化石油机械股份有限公司研究院， 湖北 武汉 430205)

引言

天然气压缩机在石油化工领域是必不可少的关键设备之一。自2014年以来，液压式天然气压缩机在加气子站压缩机市场发展较为迅速，国内学者对机械往复式和液压式天然气压缩机技术进行了充分的对比[1-4]，液压式具有可靠性高、运行平稳、噪声低及维护方便等优点。

气阀是压缩机的核心部件，与活塞式压缩机的网状气阀不同，锥阀由于其结构简单，是液压式压缩机常用气阀类型，其性能好坏直径影响到压缩机的进排气量和工作效率。根据阀芯结构不同， 锥阀可以分为全锥型锥阀和平台型锥阀。其中，平台型锥阀是由全锥型锥阀的阀芯锥部截断得到。目前，国内外对锥阀流场和动力学特性做了大量研究[5-10]：VAUGHAN等[11]利用有限体积法仿真分析了不同结构参数时锥阀的流场特性；曹秉刚等[12-13]利用边界元方法仿真分析了锥阀的内部流场特性；雷红霞等[14]利用Fluent软件研究了不同结构参数下阀芯内流体的流动特性；郑淑娟[15-16]采用Fluent软件对平台型锥阀的出流特性进行了研究，建立了阀芯大行程时过流断面面积的计算方法。上述研究主要针对液压锥阀进行了比较详细的分析，随着天然气开采的不断发展，气动锥阀越来越多的应用于压缩机上，例如液压压缩机，当流体介质发生变化时，锥阀的内部流场以及流量等特性也会发生相应的变化；但对于锥阀的结构参数优化，并未进行深入的研究。

本研究主要针对平台型锥阀进行研究，利用CFD流场仿真分析和理论建模结合的方法，建立了锥阀流通面积的理论模型。基于AGA8状态方程，分析了气体组分与流通能力的关系。最后，根据流通面积模型，对锥阀结构参数进行了优化。

1 几何结构

液压式天然气压缩机气阀结构，如图1所示，主要由阀体、阀芯、调节螺母和弹簧组成。当阀芯两侧的压差大于弹簧施加的预紧力时，阀芯向左运动，气阀打开，气体通过气阀内的流道进入压缩机气缸或者从气缸排出，完成进气或者排气过程；当阀芯两侧的压差小于弹簧力时，气阀关闭。

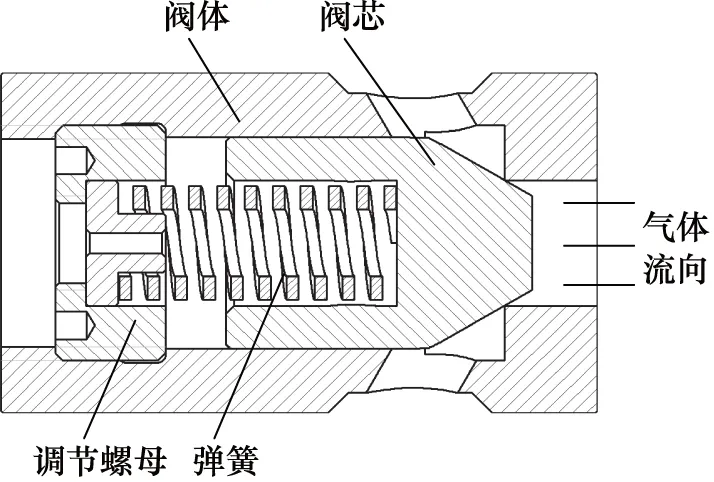
图1 液压式天然气压缩机气阀

2 流通面积计算

气阀开启过程如图2所示，假定锥阀没有倒角，密封方式为线密封，其中：dr表示锥台直径，α表示气阀锥角，ds表示阀座直径，x表示阀芯的升程。 图2a表示气阀初始密封位置，即气阀处于关闭状态，此时气阀流通面积为0。当气阀两端的压差大于弹簧预紧力，气阀开启，如图2b所示，此时气阀流通面积为以AB为母线的锥台侧面积。随着气阀开启高度的不断增加，B点可能会落在C点的下方，如图2d和图2e所示，如果继续按照图2b所示计算流通面积是不合理的，此时流通面积存在两种定义方式，一是直接连接A点和C点，流通面积为以AC为母线的锥台侧面积，如图2d所示。 二是通过A点作A′C的平行线，然后C点向平行线做垂线，流通面积为以CC′为母线的锥台侧面积，如图2e所示。

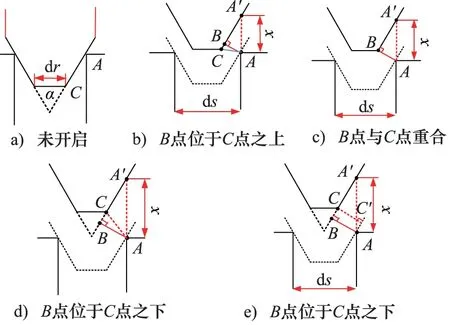
图2 气动平台型锥阀开启过程示意图

通过图2和上述分析可知，气阀的流通面积计算需要考虑3种不同的情况，即图2b、图2d和图2e。下面将分别针对上述情况建立气阀流通面积计算模型。

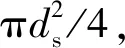
(1)

(2)

式(1)和式(2)表明，xlim和dlim是关于锥角α和阀座直径ds的函数，气阀结构发生变化时，xlim和dlim随之改变。

(3)

其中:

(4)

锥台直径dr>dlim时，B点在C点下方，通过前面分析可知，存在两种流通面积定义方式，分别如图2d和图2e所示。图2d所示流通面积用S2表示，图2e所示流通面积用S3表示。

当采用图2d方式定义流通面积时，气阀的流通面积是以AC为母线的锥台侧面积，流通面积表示通过方程计算。

(5)

其中:

f2(x)=

(6)

当采用图2e方式定义流通面积时，气阀的流通面积是以CC′为母线的锥台侧面积，流通面积表示通过方程计算:

(7)

其中:

(8)

上述流通面积公式中，xdr表示B点与C点重合时气阀的升程，可以通过如下计算：

(9)

图3计算了不同流通面积模型时，气阀流通面积随阀芯升程的变化规律。其中，气阀结构参数如表1所示。通过比较可以发现，气阀全开时，不同计算模型气阀的极限升程xlim是不同的。其中，以AB为母线时，气阀的极限升程最大，达到11.713 mm，以AC为母线时，气阀极限升程为6.128 mm，以CC′为母线时，气阀极限升程为7.537 mm。

表1 气阀结构参数

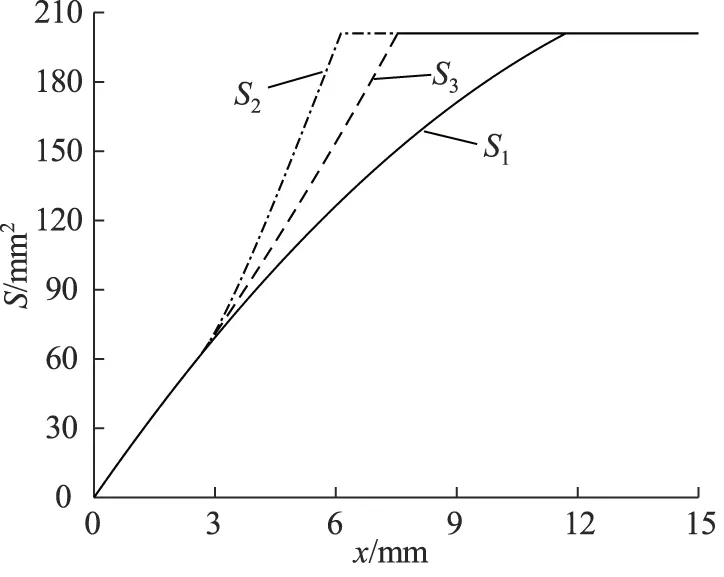
图3 流通面积随阀芯升程变化曲线

3 CFD流场分析

第二节建立了气阀流通面积理论模型，通过上节的分析可知，当气阀升程较小时，即B点在C点上方时，流通面积可以利用公式得到。但是，当气阀升程增大，B点在C点下方时，流通面积存在两种不同的模型。对于本研究的气动平台型锥阀，需要确定具体流通面积计算模型。将采用CFD流场分析方法，对气阀的流场特性进行研究，通过计算气阀不同升程时气体的质量流量，确定气阀流通面积的计算模型。仿真时，气阀流场计算采用k-ε模型，求解利用density-based方法，其中气体为空气，具体组分见表2。气阀入口端压力为3.1 MPa，出口端压力为3 MPa，温度设定为25 ℃,当气阀两端压差为0.1 MPa时，不同升程条件下，气阀内部流场特性如图4所示。通过比较可以看出，当气阀升程小于等于4 mm时，流通面积与图2b的定义基本一致，当气阀升程大于6 mm时，气阀流通面积基本保持不变。

图4 气动平台型锥阀内部流场特性

为了准确的确定气阀流通面积计算模型，利用CFD方法计算了特定压差条件下，气阀质量流量与升程的关系曲线，如图5所示。气阀质量流量随着升程的增加而增大。当升程大于6.2 mm时，质量流量基本保持不变。根据气体质量流量公式[17-18]：

(10)

其中,S表示气阀流通面积，Cq表示流量系数，pup表示进气压力，Tup表示进气温度，Zup表示压缩因子，k表示过程指数，当气阀两端的压力一定时，气体质量流量与流通面积成正比，这表明当气阀升程超过6.2 mm时，流通面积基本保持不变，且达到极限升程。

图5 不同压差下，质量流量与气阀升程曲线

通过比较图3和图5可知，当B点在C点下方时，采用以AC为母线的锥台侧面积计算气阀流通面积更准确，即针对本研究中分析的气阀，流通面积模型应该采用公式(5)。

4 仿真结果分析

压缩机进气和排气是一个动态的过程，并且气体的压力和温度会随着实际工况发生变化。 根据工况不同，气体压力有时会达到十几兆帕，甚至几十兆帕。此时，气体的物性参数会发生变化，不能简单的按照理想气体进行计算，否则会导致计算结果与实验结果产生较大的误差。根据流量计算公式可知，气体质量流量计算时需要确定压缩因子、过程指数等物性参数。AGA8状态方程是国际标准组织推荐的一种计算工作状态下天然气物性参数的方程，该方程具有计算精度高，使用范围广等特点。AGA8状态方程是基于天然气容量性质可由组成来表征和计算的概念所建立，该方程是扩展的维里方程。组成、压力和温度用作计算方法的输入数据。该计算方法需要对气体进行详细的摩尔组成分析。本研究采用AGA8状态方程计算相关物性参数，分析不同气体组分对气阀流通能力的影响。

AGA8状态方程可以表示为[19-20]：

(11)

p=ρmZRT

(12)

图6和图7计算了不同压力下，气体压缩因子和过程指数与气体组分的关系，相应的各个气体组分如表2～表5所示。通过比较可以发现，实际气体的压缩因子要比理想气体小，理想气体压缩因子等于1。另外，气体压缩因子和过程指数并不是一个定值，而是随着压力的变化而改变，其中压缩因子随着压力的增大而减小，而过程指数随着压力的增大而增大。因此，在计算气体流量等输出参数时，应该考虑物性参数变化的影响。

图6 不同压力下，压缩因子随气体组分变化曲线

图7 不同压力下，过程指数随气体组分变化曲线

图8描述了气阀内部压力变化云图，其中进气口压力为3.1 MPa，压差设定为0.1 MPa。通过该图可以看出，由于气阀流道结构的影响，气体在流道内流动时，会产生压力损失。气体在通过流通面积时，压力比进口压力小，大约为3.06 MPa。

图8 气阀内部压力分布云图

图9 不同升程下，质量流量随气体组分变化曲线

表2 气体1各组分的摩尔分数

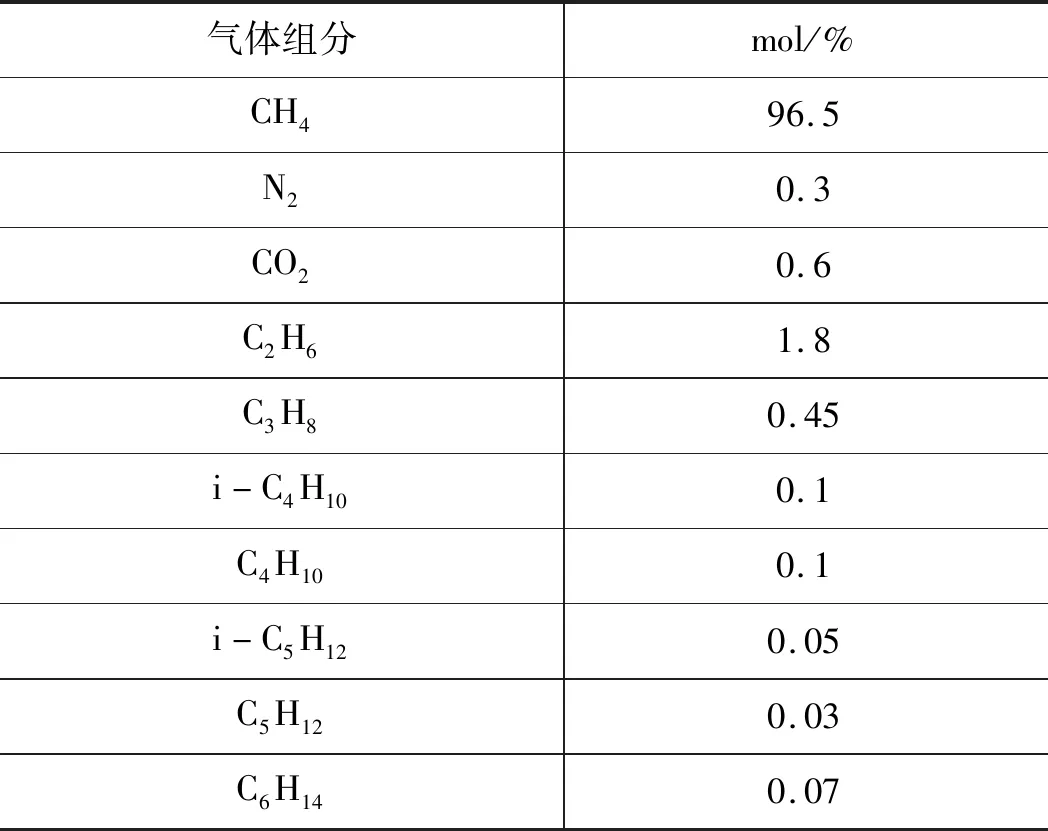
表3 气体2各组分的摩尔分数

表4 气体3各组分的摩尔分数

5 结构优化

压缩机运行过程中，气阀周期性开启和关闭。 由于压缩机运动频率较高，需要气阀在较短的时间内达到全开状态，保证压缩机的排量。因此，在设计气阀时，应该减小极限升程xlim的数值，即气阀全开时，对应的xlim要小。根据公式可知，xlim可以表示为:

(13)

通过上述表达式可以看出，xlim是关于ds，dr和α的函数。假定气阀的最大流通面积不变，即ds为常数，xlim的变化规律如图10所示。为了更加清晰的观察xlim随dr和α的变化趋势， 图11绘制了xlim相应的等高线。从图中可以看出，当dr一定时，xlim与锥角α成负相关，当α<2时，xlim随着dr的增大逐渐减小。

表5 气体4各组分的摩尔分数

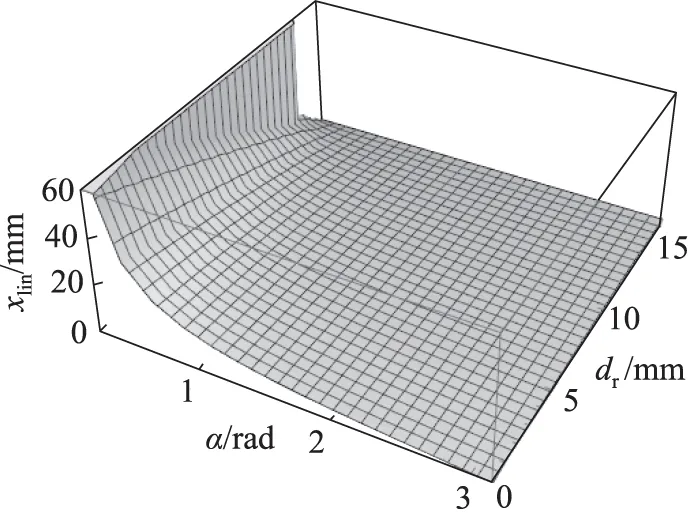
图10 xlim变化规律

图11 xlim等高线

根据前面的分析可知，气阀结构参数优化的目标是确定一组(dr,α)，使得气阀流通面积最大时xlim取最小值，可以表示为：

目标函数：

Minxlim

(14)

约束条件：

α0<α<π

dr0

(15)

其中，α0,dr0表示实际加工中的最小值，β∈(0,1)。

图12和图13计算了α0=π/18和dr0=1时，气阀的最优结构参数和xlim随β的变化规律。从图中可以看出，随着β的增大，xlim减小，而锥角α和锥台直径dr逐渐增大。

图12 xlim与β关系曲线

图13 结构参数与β关系曲线

图14中表示不同结构参数下，气阀流通面积升程的变化规律。 通过比较可以看出，气阀结构参数优化之后，达到全开时升程变小，说明气阀开启速度提升，并且β越大，开启速度越快。

图14 不同结构参数下，流通面积随升程变化曲线

6 结论

通过分析天然气压缩机气阀的几何结构，建立了气阀流通面积计算的理论模型。利用CFD仿真方法，分析了不同升程条件下，气阀内部流场的变化规律，得到了不同压差时，气阀升程与气体质量流量的关系曲线，为流通面积模型选择提供理论依据。 基于AGA8气体状态方程，得到了实际气体质量流量的表达式，计算了相同压力下，不同气体组分对气阀流量质量的影响。根据流通面积模型，提出了气阀结构参数优化方法，得到了极限升程、最优锥角和最优锥台直径随参数β的变化趋势，为气阀的结构设计和优化提供指导。