基于正交试验的风道加热器流场及温度场分析

李鑫鑫， 吴 娟， 高贵军， 邢亚东， 闫志超

(1.太原理工大学 机械与运载工程学院， 山西 太原 030024；2.矿山流体控制国家地方联合工程实验室， 山西 太原 030024；3.山西省矿山流体控制工程技术研究中心， 山西 太原 030024)

引言

风道加热器具有风阻小、加热均匀、热交换效率高等特点，在航空航天、化工等领域应用广泛。风道加热器前置离心式通风机为其供风，风机将外界的新鲜空气通过进风筒经两级导流板送入设备内部，气体在导流板的作用下一方面延长了与翅片加热管道的接触时间，另一方面也可使加热管表面温度更加均匀，避免因局部温度过高损伤加热管。实践应用表明导流板的长度和开口角度对风道加热器流场和温度场的性能参数均有影响。

许晓红等[1]对换热器结构进行仿真，探究不同结构下设备的流场均匀度和性能参数。冯军红等[2]通过数值模拟的方法探究了不同氧化剂对空气加热器出口流场的影响。靳遵龙等[3]利用流体力学软件研究了螺距和肋高对换热器速度场和温度场的影响。

以上研究主要集中在加热管的结构和加热介质对加热器的影响方面，现阶段，关于入口通流部件的结构即导流板的长度和开口角度对风道加热器的性能、流场和温度场方面的研究较少。

本研究以煤矿主通风系统用风道加热器为研究对象，在Fluent中通过四因素三水平正交试验法模拟了两级导流板不同开口角度和长度对风道加热器压降、温升的影响，为优化其结构提供参考。

1 正交试验设计

1.1 试验目的

为提高风道加热器的温升和加热效率，降低气体流过风道加热器的压力损失，本研究通过正交试验，以温升和压降为评价指标，对风道加热器的结构设计进行优化，表1为设备的基本参数。

表1 风道加热器基本参数

1.2 试验因素及方案

风道加热器进口处布置有4块导流板，内侧的两块为第一级，外侧的两块为第二级，两级导流板均沿中间截面呈对称分布，定义导流板与中间截面的夹角为导流板的开口角度，定义导流板在水平方向的投影为导流板的长度。本研究将第一级导流板角度、第二级导流板角度、第一级导流板长度、第二级导流板长度这4个因素定义为正交试验的水平因素。根据工程实践可知4个参数的取值范围，并制作了如表2所示的影响因素和水平设计表[4]，然后根据表2设计了如表3所示的L9(34)正交试验表[5]，共9组试验方案，其中试验序号6为现有风道加热器结构。

表2 影响因素和水平设计表

表3 正交试验设计

2 数值模拟

2.1 数学模型

本研究采用Fluent软件对9种正交试验方案进行定常模拟，风道加热器在进行流动与传热的数值模拟时应遵循流体动力学基本控制方程即能量、动量和质量守恒方程[6]，其中能量守恒方程如下：

(1)

式中，ρ，T，V分别为密度、温度和体积；λ代表流体的导热系数；Cp为定压比热；ST为黏性耗散项。

同时风道加热器内部存在复杂的内流动如湍流、涡流等，气体流动的各向异性很高，本研究选用RNGk-ε湍流模型进行模拟。与标准k-ε湍流模型和Realizablek-ε湍流模型相比，RNGk-ε湍流模型能更好的模拟湍流且各向异性高的流动过程[7]。

2.2 模型建立

风道加热器由进风筒、第一级导流板、第二级导流板、W型翅片加热管、保温层和出风筒6部分组成，保温层材料采用硅酸铝棉，加热丝采用镍铬合金丝，其他材质为Q235，风道加热器及离心式通风机实物图，如图1所示。

图1 风道加热器及离心式通风机实物图

风道加热器长1500 mm，宽和高均为750 mm，为避免数值模拟过程中出现回流，在原有出风筒的基础上增加1000 mm的风筒作为延长的计算域。为研究两级导流板不同角度和长度对风道加热器流场和温度场的影响，按照正交试验法并结合设备实际尺寸在SolidWorks中建立了不同导流板开口角度和长度的风道加热器三维流场模型。试验序号6即现有设备的三维模型如图2所示。

图2 风道加热器三维模型

2.3 数值计算方法

将9种试验方案的网格模型导入Fluent软件中进行定常模拟，激活能量方程，设计工况下雷诺数为380948，流动方式属于湍流，选用RNGk-ε湍流模型。分别定义Q235、硅酸铝棉、不锈钢304无缝钢管和镍铬合金丝的材料属性，设置加热丝为发热源[8]，输入体积功率为10255433 W/m3。

现场采用4-72-4.5 A的7.5 kW变频离心式通风机为风道加热器供风，将实际条件下离心式通风机出口的压力和流量作为风道加热器仿真的入口条件，以确保仿真与实际情况相一致。选用压力入口、速度出口的边界设置，由于Fluent中没有速度出口，故设置速度入口，速度值设置为-12.37 m/s，入口和出口的初始温度均设置为298 K。风道加热器内部壳体和加热管设置为传热耦合面[9]，求解方法选用SIMPLE算法和标准压力，收敛残差均设置为0.00001，初始化后求解计算。

2.4 网格划分及无关性验证

将9种试验方案的三维模型分别导入ICEM CFD软件中进行网格划分，与设备整体尺寸相比，36支W型加热管的尺寸较小，为保证网格划分的质量应对其进行加密处理。另外，进口和出口部位的变径部分由于结构突变较大也应采用局部细化处理，其他部分的网格尺寸设置为10～30 mm不等。为减少网格数量，缩短数值模拟的计算时间，采用四面体网格和六面体网格联合的方法完成网格划分。

为验证数值模拟的正确性，避免因网格数量不同而对数值模拟结果产生影响，对试验序号6即现有风道加热器分别划分了5种不同数量的网格模型，并进行了网格无关性验证，所得计算结果如表4所示。由表4可知，当网格数量达到567.9万时，随数量的增加，温升基本不变，综合考虑温升和数值模拟的时间，选择第3种方式进行网格划分。

表4 网格无关性验证

按照第3种网格数量的划分方式对9种试验方案的风道加热器模型进行网格划分，得到的网格数量在566～568万不等，且网格质量均在0.23以上，试验序号6的全流场网格模型如图3所示。

图3 风道加热器全流场网格模型

3 数值模拟正交试验结果分析

3.1 直观分析

表5为正交试验9种试验方案的数值模拟结果，与原方案(试验序号6)相比，试验7、8和9没有达到优化的目标。通过对比9种试验方案的结果， 试验序号1即试验方案为A1B1C1D1时两种评价指标均达到最佳， 与原方案相比温升增加了2.43%， 压降即压力损失减少了15.56%。

表5 基于正交试验的数值模拟结果

3.2 极差分析

表6为对正交试验的数值模拟结果进行的极差分析，其中R为极差值，它表示该因素对评价指标的影响程度，R的值越大，该因素对评价指标的影响越显著。K1，K2，K3分别对应水平1，2，3的数据和，k1，k2，k3分别对应水平1，2，3数据的综合平均[10]。

从表6中可以看出，4个因素对温升影响的显著顺序为A>B>D>C，即第一级导流板角度对温升的影响最显著，第一级导流板长度对温升的影响最弱。各因素对压降影响的显著顺序为B>A>D>C，即第二级导流板角度对压降的影响最显著，第一级导流板长度对压降的影响最弱。

图4、图5分别为各因素各水平对温升和压降的影响趋势，从两图中可以看出，在两级导流板角度对两个评价指标的影响方面，温升随第一、二级导流板角度的减小而增大，压降随第一、二级导流板角度的减小而降低，温升和压降均在角度为第1水平时达到最佳；在两级导流板长度对评价指标的影响方面，温升和压降在第一级导流板长度为第2水平，第二级导流板长度为第1水平时达到最佳。

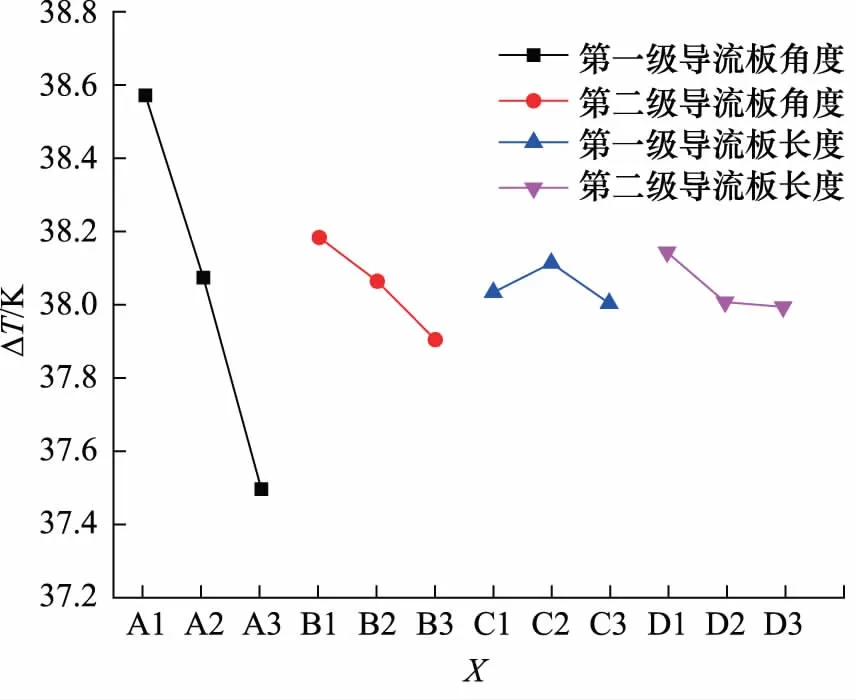
图4 各因素各水平对温升的影响趋势

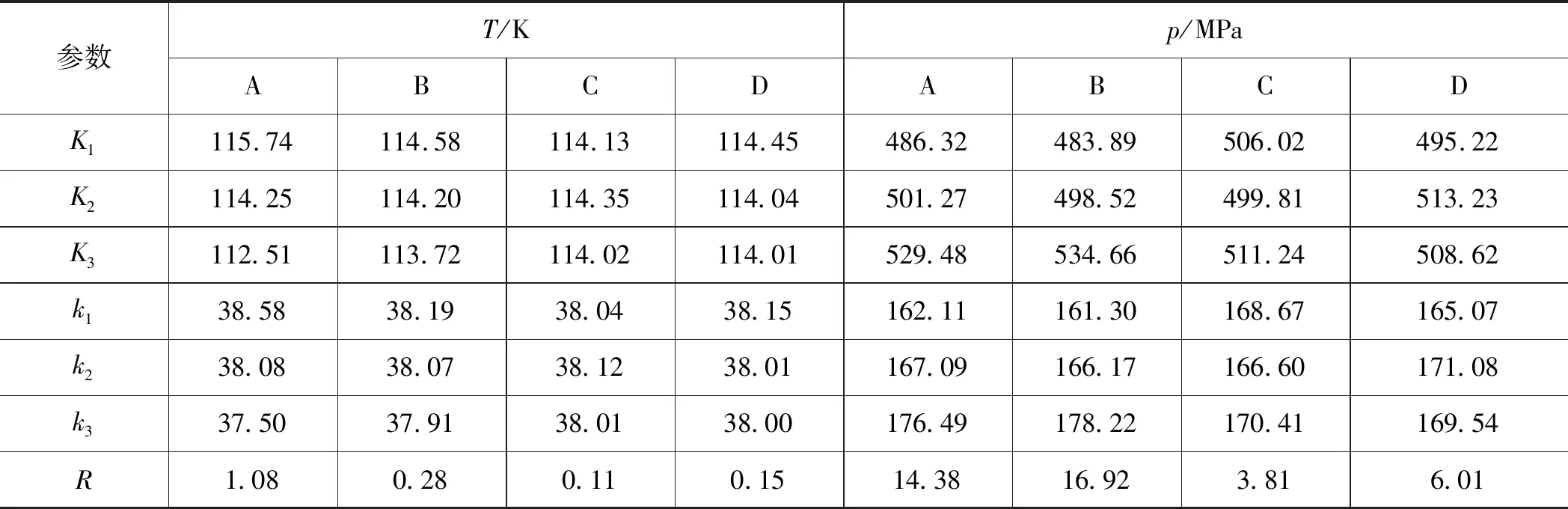
表6 正交试验的数值模拟结果极差分析

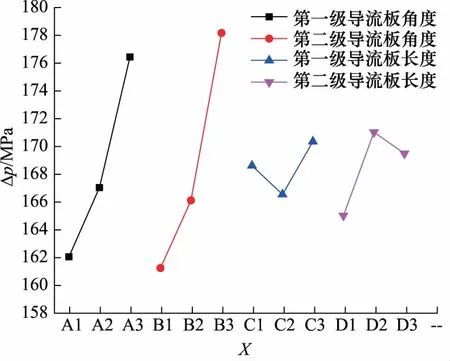
图5 各因素各水平对压降的影响趋势

综上所述，正交试验的最优组合为A1B1C2D1，此时第一级导流板角度为21°，第二级导流板角度为27°，第一级导流板长度为170 mm，第二级导流板长度为150 mm。

4 数值模拟优化结果分析

在SolidWorks中建立最优组合A1B1C2D1的三维流场模型，并在Fluent中按照相同的边界条件进行数值模拟，得到的温升为38.86 K，比优化前提高了2.59%，压降为1.5076×10-4MPa，压力损失比优化前降低了15.95%。

图6为去掉延长计算域后的风道加热器优化前后水平中间截面的速度流线云图， 优化前后均是入口和出口区域的速度较高，这是由于入口尺寸较小，气流在此处比较湍急，进入空间较大的箱体内部后流速放缓，流经出口时尺寸再次减小，流速随之增大。

图6 优化前后水平中间截面的速度流线云图

优化前在靠近入口处的两侧形成2个明显的涡流，这是由于气流从入口进入箱体后中部的主流受到加热管的阻拦后，部分气流向两侧延伸，再次受到箱体壁面的阻拦后，变为与主流方向相反的回流，回流与主流在入口两侧发生接触，形成涡流[11]。优化后由于两级导流板开口角度减小，长度增加，使入口两侧的涡流明显减轻，减少了气体的压力损失，气流更加平稳，湍流动能减小。

图7～图9分别为优化前后出口截面的全压、湍流动能和温度场分布云图，优化后由于涡流减弱[12]，压力损失降低，中间区域的全压明显增加，气流不稳定性减小，湍流动能随之减小，温度也随之升高，这与图6中气体内部的流线云图相一致。

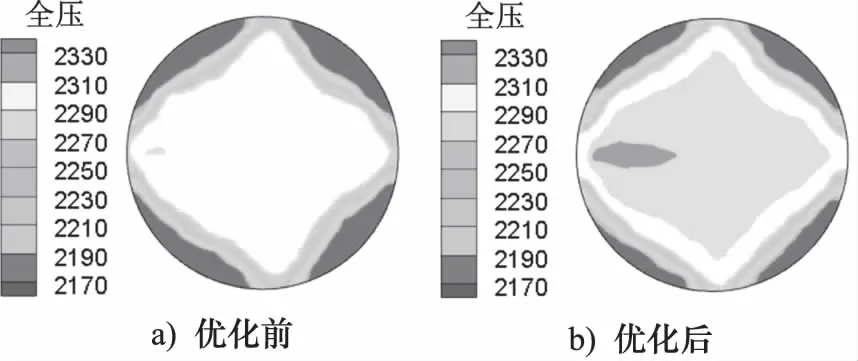
图7 优化前后出口截面的压力云图

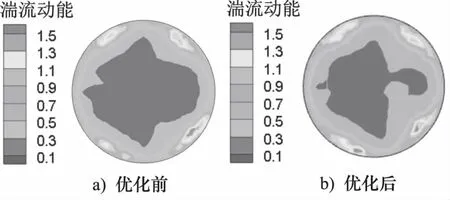
图8 优化前后出口截面的湍流动能云图

图9 优化前后出口截面的温度场云图

5 结论

本研究通过L9(34)正交试验对风道加热器结构进行优化，并将优化前后的风道加热器性能进行对比，得出以下结论：

(1) 第一级导流板角度对温升的影响最显著，第二级导流板角度对压降的影响最显著；

(2) 当第一、二级导流板角度分别为21°和27°，长度分别为170 mm和150 mm时，风道加热器结构达到最优，且与优化前相比温升提高2.59%，压力损失降低15.95%。

(3) 优化后风道加热器内部涡流减弱，压力损失降低，湍流动能减小，气流更加平稳。