图形直观在“函数及其表示”中的呈现

杜剑南 王鑫

[摘   要] 文章通过比较分析普通高中数学课程标准实验教科书人教A版与北师大版“函数及其表示”这一节的内容，得出两个版本的教科书在图形直观呈现方面有以下特点：都利用图形直观呈现“函数及其表示”的相关内容，但是在函数概念的引入方式、函数的表示方法、函数概念的发展历程、课后习题四个环节上的呈现各具特色。研究结论：人教A版与北师大版在“函数及其表示”一节中以图形直观呈现相关内容; 图形直观呈现函数概念时内容和位置不同;图形直观呈现映射概念时方式和内容不同;图形直观呈现函数概念的发展历程时视角不同;图形直观呈现课后题时内容、形式和数量不同。

[关键词]图形直观;函数及其表示;应用;高中教材

[中图分类号]    G633.6       [文献标识码]    A        [文章编号]    1674-6058（2020）03-0044-04

随着“几何直观”在《义务教育数学课程标准（2011年版）》中的提出[1]，“直观”的概念越来越受到人们的重视。对于数学直观 ，M·克莱因认为，“数学不是依靠在逻辑上，而是依靠在正确的直观上”[2]。作为体现直观的重要载体——教科书，成为研究者们的重要研究对象。教科书作为依据课程标准和学生接受能力编写的教学材料，是课程目标与教学内容的具体体现，在一定程度上决定了学生的学习机会和学业成就，函数概念在数学及中学数学课程中具有重要地位。自变量数学产生以来，函数概念一直处于数学的核心地位。德国数学家克莱茵（F.klein）称函数为数学的灵魂。在整个函数教学过程中，又以函数概念为学校教学和学生学习中最难掌握的内容。在此基础上，本文提出从图像和表格相结合的图形直观的概念着手，通过对教科书之间图形直观在引入函数概念、引入映射概念、阐述函数概念的发展历程以及课后练习和习题四个部分呈现的特点的比较，进一步强化数学课表中提出的直观的概念，以引入图形的表示方法来探究高中函数的教与学，为高中的“函数概念”教学提供参考和建议。

一、研究对象与方法

1.研究对象

研究对象为人教A版与北师大版教材中关于“函数及其表示”的内容。比较的具体内容见表1。

需要说明的是，人教A版教材中映射概念在“函数的表示法”中出现，而北师大版教材则通过独立的小节引入映射概念。

2.研究方法

运用比较研究法，从函数概念的引入、映射概念的引入、函数概念的发展历程和课后练习和习题四个维度进行研究分析，将教材中有关图像和表格展示的部分提取出来，作为图形直观的例子进行分析，从而揭示图形直观的不同呈现在函数概念内容处理中的应用。

二、研究结果与分析

1.两个版本教科书在图形直观呈现方面存在共性

通过对两个版本教科书中的图像和表格进行提取，可以明显发現，不管是人教A版还是北师大版教材都利用图像和表格的形式（即图形直观）来呈现“函数及其表示”这一节的内容。

2.两个版本教科书在图形直观呈现方面存在差异性

虽然两版本教科书都利用图形直观呈现“函数及其表示”这一节的内容，但是比较后发现，“函数概念引入方式”“映射概念的表达”“函数概念的发展历程呈现”以及“课后练习和习题”在图形直观呈现时，在表现方式、图表内容、图表数量、图表位置（相应概念的前后）以及阐述视角上都存在明显的差异。

（1）图形直观在引入函数概念中的呈现

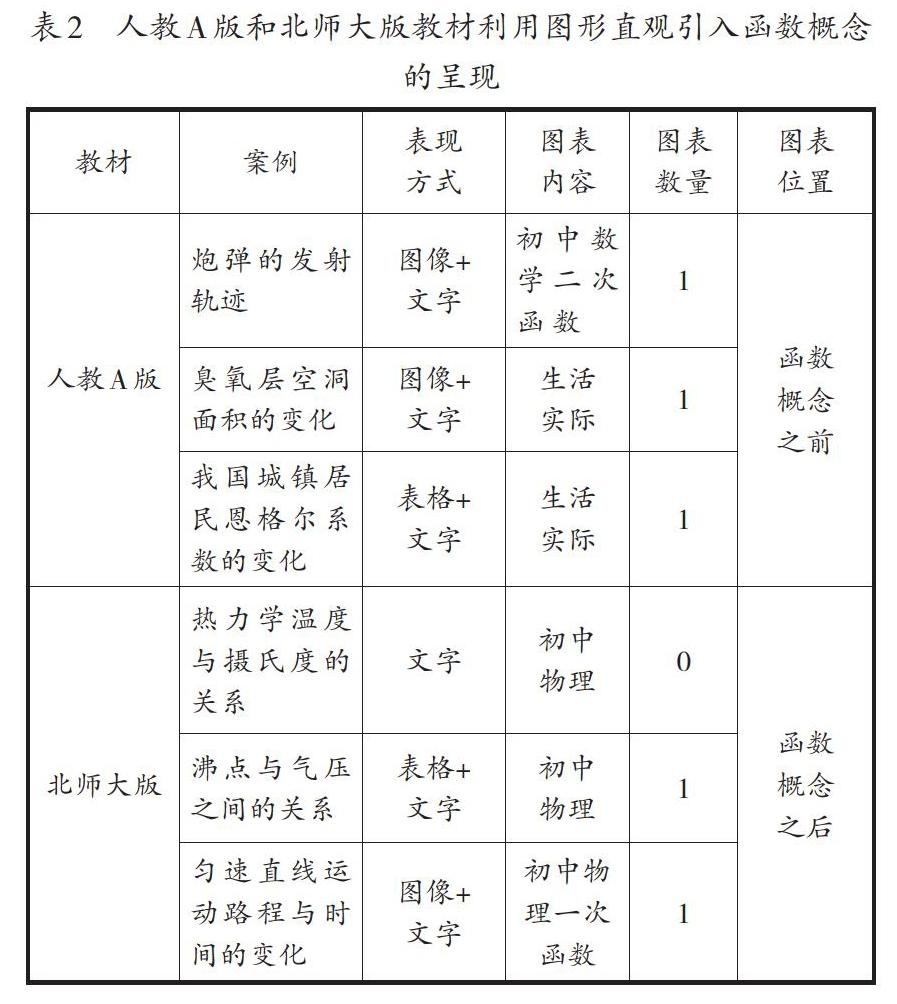
人教A版和北师大版教材利用图形直观呈现函数概念的方式见表2。

通过表2可以看出，人教A 版教材通过三个案例呈现函数的相关概念，呈现案例时加入了图形直观，值得注意的是人教A版在加入图形直观时所呈现的是学生熟悉的二次函数图像。利用图形直观的表现形式主要为图像与表格两种，每个案例都有相应的图表展现;函数概念的定义放在图表案例之后。

北师大版教材则是先提出函数的相关概念，再呈现三个图表案例，但是在热力学温度与摄氏度的关系这一案例中并没有涉及图形直观;在利用图形直观的表现形式上，采用图像与表格的两种形式。值得注意的是，北师大版教材在呈现图形直观时，明确地提出三个案例都是初中物理当中所学过的内容。

（2）图形直观在引入映射概念中的呈现

人教A版和北师大版教材中映射概念的呈现如表3所示。

通过表3可以看出，人教A版教材在呈现映射概念时没有利用图形来理解映射概念，而是从函数的概念上理解映射的概念，并利用两个生活中的案例加以说明，让学生能够在案例中理解“一一对应”的关系。

北师大版教材则是利用了映射图呈现映射概念，并且举例形式更为多样化，不仅加入了生活中的事例，还加入了集合的案例，让学生在实际生活和数学中清晰体会映射的概念。

在内容设置上人教A版教材有“思考”栏目，北师大版教材有“思考交流”栏目，这些栏目要么是为引入知识作铺垫，要么是为巩固知识服务。北师大版教材的栏目中也可看到图形直观的影子，说明图形直观可以帮助理解映射概念。

（3）图形直观在阐述函数概念发展历程中的呈现

数学史作为传播数学文化的重要载体，是新课标下理解数学的一种新途径。普通高中《数学课程标准》（实验）中指出，“数学是人类文化的重要组成部分，数学课程应适当反映数学的历史、应用和发展趋势。众所周知，每个数学概念和公式的背后都有着它的故事，而且这些故事也能引发后人更多的猜想。人教A版和北师大版教材中阐述函数概念发展历程的呈现如表4所示。

由表4可以看出，人教A 版和北师大版两个版本的教材在阐述函数概念发展历程中都未涉及图形直观的内容，但是北师大版教材在“阅读材料”这个栏目当中揭示了函数概念的发展——从解析式到图像到对应关系。从中可以看出，图像在函数概念的发展上起到了承前启后的关键作用，也奠定图形直观在学习函数时的基础地位。人教A版教材则是先结合现实生活中的实际案例，阐述函数产生和发展的背景，再利用数学家对函数变量的认识将函数进行反复的定义，最终用集合和对应语言定义函数概念，与本节内容相衔接，为学习者提供理论基础。

（4） 图形直观在课后练习和习题中的呈现

习题是数学教学的重要组成部分，是学生学习过程中不可或缺的重要环节，是学生掌握知识、形成技能、发展能力的主要载体，也是提高学生运用知识解决简单实际问题能力的有效工具。人教A版和北师大版教材图形直观在课后练习和习题中的呈现如表5所示。

由表5可以看出，人教A版教材在函数概念这一节中未设置有关图形直观呈现的相关习题，但是在习题1.2中却设置了7道有关图形直观呈现的题目。通过对比可以发现，题目利用不同的表现方式对初中和高中所学的函数图像进行考查，与此同时也利用函数图像解决相关的数学问题，展现了图形直观呈现方式的灵活性。北师大版教材设置了4道利用图形直观呈现的题目，在习题设置上明显少于人教A版教材，在函数概念和映射的课后习题以及本节习题中也都设置了相应的题目。除此之外，教科書还考查了学习者对映射图的理解以及设置了如何利用表格求解定义域和值域的问题。

三、研究结论及建议

1.结论

通过比较分析普通高中数学课程标准实验教科书人教A版与北师大版“函数及其表示”这一节的内容，图形直观的呈现情况如下。

（1）通过对比可以看出，两个版本的教科书在设计“函数及其表示”这一节中，无论在概念的引入、映射的表示还是课后的练习题中，都呈现了相应的图像以及表格，也由此说明图形直观的呈现在“函数及其表示”中的重要性，应该引起教学者和学习者的高度重视。

（2）人教A版与北师大版教材都采用不同图形的例子呈现函数概念，但是在图形的内容以及图形所在位置方面存在明显的差异。虽然两个版本教材都十分重视高中知识与初中知识的衔接，让学生用熟悉的初中知识理解高中的概念，但在内容上，北师大版教材与初中知识衔接更为紧密，并且与初中物理相结合，加强了学科之间的相互联系。在图形位置方面，人教A版教材将图表放在函数概念的定义之前，体现“以形释意”的过程，从图形出发，理解函数概念;北师大版教材先提出函数的概念再引入图表，体现先观察后反思的过程，从函数概念出发，再通过相关图形深化理解。

（3）在呈现映射概念的方式上，人教A版教材使用文字描述，而北师大版教材使用图形加文字综合描述，以图形的方式可以直观展现映射概念中的“一一对应”关系。在呈现映射概念的内容上，北师大版教材与人教A版所举案例都跟生活实际相联系，加入了之前所学的集合概念，使得学习者在学习函数的概念时，与所学过的集合相联系，让学习者整体地认识函数。

（4）人教A版与北师大版教材都注重对于数学史的应用，但是在引入数学史的过程当中，两个版本的教材存在差异。相比较而言，人教A版教材的特点是在阐述函数概念的发展历程时更为注重数学知识的系统性和全面性，让学生明白知识的来龙去脉。北师大版教材的特点则是注重利用数学史引发学生的阅读兴趣，从历程这个大的方向，抽出一个有意思的篇目，让学生明白为什么函数的概念会变成现在的“对应关系”。

（5）函数概念本身就具有抽象性，利用图形直观在不同位置的不同呈现方式，可加深学习者对函数概念的理解。人教A版教材在“函数概念”后的练习题中并没有涉及与图形相关的问题，此外，在习题1.2中以初中及高中新学习的函数为题，让学习者画出以上函数的图像，通过画出相应图像，将新学习的知识与初中知识相联系，提升学习者对函数的整体认识。北师大版教材虽与人教A版教材相同，都选取了初中所学的知识，但是选取的内容为梯形的面积（几何角度），在形式上也加入了利用表格作图的题目，使学习者能深刻体会函数概念。另一方面，在利用图形直观解决问题的题目数量上：人教A版教材在习题中共设置了8道与图形相关的问题，明显多于北师大版教材。

2.建议

（1）由于两个版本的教材在“函数及其表示”一节中以图形直观呈现相关内容，所以说明利用图形直观可以帮助学生理解函数的相关概念。因此，教师在讲授这一部分内容时，应该加入更多图形的相关案例，帮助学生理解函数的相关概念，从而达到图形直观的目的。

（2）在教学中可以尝试多用初中所学的函数图形呈现函数的概念。数学图形是数学学习中的一项重要内容，合理地利用数学图形也能从整体上提升学生对数学知识的理解。建议教师在呈现函数概念时，可以加入初中学过的具体函数，甚至以具体函数的图形来认识函数的概念。这样既可以提升学生对于函数概念的理解，又可以将初中与高中的知识进行整合，体现数学知识的整体性。

（3）在教学中利用映射图呈现映射概念，理解“一一对应”。把映射生活化或图表化的方法也是高中数学课程中需要学生掌握的方法，建议使用人教A版教材的教师在引入映射概念时，利用北师大版教材所设计的映射图的方法，让学生以图形理解概念，体现图形直观在数学概念理解中的作用。

（4）在呈现函数概念的数学史中，应加入具体函数图形演变的过程。研究者建议在教科书修订或教学中可以尝试把两种方式相结合来阐述函数概念的数学史。第一，数字引导法，把不能利用以前函数定义表示的函数单独举例出来，目的是使用具体数字的形式，让学生能够直观感受到函数的定义，引发思考，也能对现在的函数定义有一个全面的认识。第二，图形描述法，即以列表、图像以及解析式表示，把函数概念的演变以图形的方式表示出来，目的是减少文字的叙述，提高学生的阅读兴趣;也能体现出数学的逻辑思维和函数概念的形成过程。图形直观对于函数概念的数学史的学习，也有其独特的意义。

（5）在课后练习题和习题的编写及教学中加入与图形相结合的习题的重要性不言而喻，数学题最能反映学生对所学知识的掌握程度，所以数学题的设置也要尽可能多地涉及前面所学的知识，但是以什么方式呈现才是我们需要解决的问题。通过对两个版本教材的分析，研究者建议在教材编写方面：更多地加入与前面所学概念相吻合的图形问题。让学生多动手画图，提升对概念的理解。在教学方面：教师应当多给学生设置一些与图形相关的问题和练习，让学生可以直观地、具体地理解“函数及其表示”这一节的概念内容，一方面丰富了数学现实化的内容，另一方面也提高了学生利用图形理解函数概念的能力。

综上，通过对两个版本的教材图形直观的呈现进行比较，可以看出：图形直观的不同呈现方式，在函数概念教学中可以帮助学生理解抽象的概念，变抽象为具体，使得学生更为容易地理解抽象事物的特征，但最好选取学生所熟知的图形，便于其理解。

[  参   考   文   献  ]

[1]  中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北 京师范大学出版社，2012.

[2]  M·克莱因.古今数学思想（第四册）[M].上海：上海科技出版社，1979.

[3]  叶立军，王晓楠.中美国高中数学教材比较研究—以“几何概型”为例[J].数学教育学报，2012（2）：49-52.

（责任编辑 诺   依）