等比数列求和公式的快速永恒记忆

■雷皖婷

大家都知道高中数学中等比数列求和公式比较难记忆，如何快速长久地记忆这个枯燥的公式是高中数学的一个难点。我在学习与记忆中发现了关于这个公式的快速记忆方法，经过实践运用，特别有效，达到了事半功倍的效果，现分享给大家。

如果一个数列从第2项起，每一项与它前一项的比等于同一个常数，这个数列就叫等比数列。这个常数叫等比数列的公比，公比通常用字母q表示(q≠0)。高中数学中等比数列前n项和的公式是，当然也可以写成。可是要记住这个公式并不容易，可能要花很多时间。有没有简单的记忆方法能帮助我们快速地而且长时间地深刻记忆呢?

一、等比数列前n 项和公式的推导过程

推导过程一般是这样的：

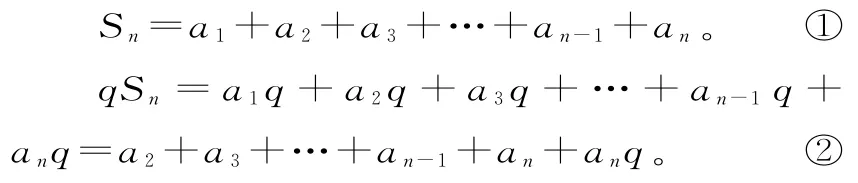
用②的两边分别减去①的两边，得到(q-1)Sn=anq-a1，当q≠1时，从而得到等比数列前n项和的公式为

二、常规记忆方法

可是我们如何记忆上面这个公式呢? 大多数同学是这样记忆的：“总和等于an乘q减去a1(的差)，除以q-1”。还有的同学记忆前面的推导过程，不记公式，这肯定是行不通的，在有限的考试时间内，还要进行推导过程，必定会耗费时间，而且万一推导出现失误，可能整道题丢分，这是得不偿失的。

三、快速长久记忆法

首先讲个命名，我们把m前面的数m-1命名为m的“小邻居”，把后面的数m+1命名为m的“大邻居”。等比数列的公比为q，因此q-1 就是公比q的“小邻居”，q+1就是公比q的“大邻居”。现在我们来记忆等比数列前n项和的公式。

有个成语叫“杀人灭口”，那么我们就用“歹徒杀人灭口”来形象记忆：“歹徒”就是躲藏在末项(an项)后面的一项，即下一项anq就是“歹徒”。“杀人”的意思就是减去首项，“歹徒”杀了“首领”。“灭口”的意思就是除以公比的“小邻居”，“歹徒”穷凶极恶，连公比的“小邻居”都不放过。利用“歹徒杀人灭口”这一形象比喻就能帮助我们把一个复杂的公式记住了，可以说能达到终生不忘的效果。只要知道“杀人灭口”这个成语，找到“歹徒”“首领”公比“小邻居”，同学们再遇到相关试题就会快速解答出来。所以学习时遇到不太好理解记忆的问题，只要我们充分发挥联想，多发散思维，就能找到解决的办法，而且还会激发学习的求知欲。

四、应用举例

1.求等比数列1，2，4，…，1024的所有项之和。

解：本题“歹徒”是1024的再后一项，即2048，公比“小邻居”是2-1=1，故所有项之和为

2.数列1，m，m2，m3，…，mn-1，…(m≠1)的前n项和是多少?

解：本题“歹徒”是mn-1的再后一项，即mn，公比“小邻居”是m-1，故所有项之和为。

本文只谈谈等比数列前n项求和的记忆方法，不展开其他讨论。

结束语：高中数学任重而道远，公式纷繁复杂，我们在学习时，只有不断地总结经验，发散思维，联想记忆，才能达到事半功倍的学习效果。本文的记忆技巧只是抛砖引玉，希望同学们还能总结出更加有效、高效、长效的其他记忆方法。