浅析高中数学中转化思想的培养

■任晶晶 唐耀平 冯 允

纵观近几年的高考数学试题，我们发现高考试题在对主干知识进行考查的同时，也突出对数学思想方法的考查，转化思想就是数学思想中最为基础和常用的思想方法之一。遇到数学问题通过直接求解或用已知模型求解都解决不了时，我们会想办法把问题转化成一个熟悉的会解决的问题，这种思想就是转化思想。转化思想贯穿于各级各类数学考试中，下面结合大家的实际学习情况，对大家转化思想的培养给出以下几点建议。

一、吃透教材，从不同的角度理解教材

2019年高考试题给我们传达了一个信息：回归教材。同学们在上课前要研究透教材，教材是学习的一个重要载体，不能只看买的辅导书，脱离教材，但是又不能拘泥于教材，需要透过教材研究更加本质的东西，对于不好理解的概念和定理我们要从不同的角度来理解。

案例1：函数的概念是什么? 映射的概念是什么?

案例2：什么是一一映射? 函数与映射的区别?

对于书本上的概念不能只满足于会背，还应该理解概念的关键和实质。北师大高中数学教材必修1 给出了函数的概念，其实概括起来满足三点的对应关系就是函数，即①非空数集A与B，②对应关系f，③“每一”对“唯一”。而映射的概念只需变换①中的“数集”为“集合”即可。这样很容易看出函数与映射的区别。映射这一节，课本上的例子用图示给出了三个对应关系，我们可以类比“射雕”来理解，我们把集合A比喻成“箭”的集合，集合B比喻成“雕”的集合，这样就可以形象直观地理解“一箭双雕”不是函数，大家产生兴趣的同时，也学到了相应的知识。关于一一映射，课本上给了我们三点需要满足的条件，当然大家不容易记住，这时候只需要记住八个字“一箭一雕，箭尽雕尽”，不需要死记课本就可以了，同学们会感觉学习起来很轻松，数学原来如此有趣。

二、培养联系知识的能力，在知识获取中渗透转化思想

现有的高中数学教材以“螺旋式”的结构编写，很多知识的学习不是一步到位，同学们要善于借助思维导图，加强新旧知识的联系，培养联系知识的能力。转化思想的培养最好的方法是学会发散思维，在联系所学知识的基础上，学会迁移，探索解题方法。

案例3：已知函数f(x)=，x∈[0，2]，求函数的最大值和最小值。

案例3是北师大高中数学教材必修1中“函数单调性”一节的一个例题，教材上给出先用函数单调性的定义证明该函数在该区间上是单调递增的，然后再求最值。这道题其实我们还可以联系以前学过的反比例函数和图像平移规律来完成单调递增的探索，把y=向左平移一个单位后就是函数f(x)=的图像(图像略)，由图像易知该函数在该区间上是单调递增的。

对于一般的一次分式函数f(x)=，同学们可以探究能不能不通过分离常数的变换和平移把其大致图像确定下来。

三、培养实践能力，在解题练习中强化转化思想

实践是检验数学知识的最佳途径，同学们在解题练习中有意识地强化转化思想，能够达到很好的培养效果。很多时候同学们的学习状态是上课听懂了，下课不会做题，之所以会出现这种现象，究其原因是同学们只停留在听懂的水平，并没有把知识内化为自己的东西，遇到新的情境不知道如何下手。所以同学们不能只满足于课堂上的学习，还要选择一些优质高效的题目，以题目为载体，多加练习，以达到强化转化思想方法的目的。

案例4：已知x＞0，y＞0，z＞0，求证：

这个题目是余弦定理的应用，很多同学第一时间想到用基本不等式来解决，但是又发现看似不难的一个题目，却无从下手。这时候如果试试用余弦定理，将看成两边分别为x，y，其夹角为60°的三角形的第三边，由此将代数问题转化为平面几何问题。

如图1 所示，在平面上任选一点P，作∠APB=∠BPC=60°，设AP=x，BP=y，CP=z，由余弦定理知，，在△ABC中，由两边之和大于第三边，可知原不等式成立。

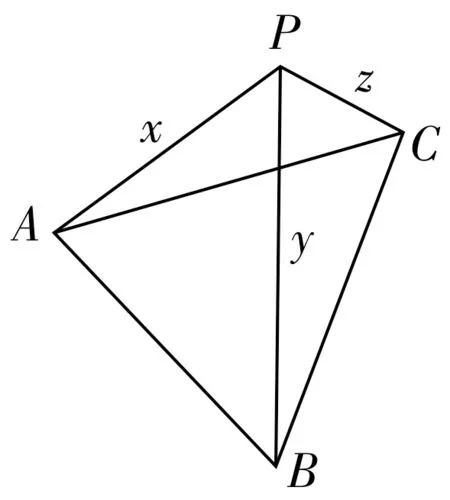
图1

四、合理研判学情，加强反思总结

2019年的高考试题已经告诉我们，只靠刷题是不行的，要加强对思维能力的培养，注意打破思维局限性，拓宽学习思路，不断地根据学习情况来反思自己的弱点，经过努力进而改变现状，只有这样才能不断提高解答数学问题的能力，提高数学解题的效率。数学问题中利用转化思想解题的例子比比皆是，同学们在平时的训练中要不断充实知识，经常进行转化思想方法的训练，针对不同的问题情境，在保证逻辑正确的前提下，大胆尝试用不同的方法去解题，这样对于数学的学习会起到事半功倍的效果。