品味高考题的一题多解
■文 明
一、研究背景
课程改革后,课时减少,习题课也大幅度减少,导致同学们接受、记忆、模仿的做题方式占主导地位。从而导致同学们出现思维定式、思维狭窄的现象,对于开拓同学们的思路、创新性的思考极为不利。而一题多解正是从相同的题目出发,利用不同的思路、不同的知识点、不同的方法而达到共同的目的,即殊途同归。一题多解是一种鼓励同学们深入思考的好方式,使同学们不仅关注已有的老思路、老想法,而且可以在已有知识的基础上尽情舒展自己的思路,可以有效地培养同学们的主动性,以及开阔同学们的思维,促使同学们去创新、去思考,使同学们逐步形成解题的灵活性与解题技巧。同时鼓励同学们在学习过程中养成独立思考、积极探索的习惯。所以,一题多解对于推动新课程的实施和培养同学们的发散思维具有重要意义。
二、一道高考题的三种解法
题目(2012 年高考山东)设函数f(x)=g(x)=ax2+bx(a,b∈R,a≠0)。若y=f x( )的图像与y=g x( )的图像有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是( )。
A.当a<0时,x1+x2<0,y1+y2>0
B.当a<0时,x1+x2>0,y1+y2<0
C.当a>0时,x1+x2<0,y1+y2<0
D.当a>0时,x1+x2>0,y1+y2>0
解法一:令=ax2+bx,则1=ax3+bx2(x≠0)。设F(x)=ax3+bx2,F'(x)=3ax2+2bx。令F'(x)=3ax2+2bx=0,则x=, 要使y=f(x)的图像与y=g(x)图像有且仅有两个不同的公共点,只需=1,整理得4b3=27a2。于是可取a=±2,b=3来研究,当a=2,b=3时,2x3+3x2=1,解得x1=-1,x2=,此时y1=-1,y2=2,x1+x2<0,y1+y2>0;当a=-2,b=3 时,-2x3+3x2=1,解 得x1=1,x2=,此时y1=1,y2=2,x1+x2>0,y1+y2<0。答案为B。
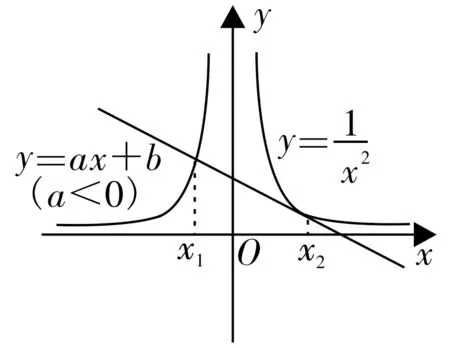
图1
解 法 二:令f(x)=g(x),可 得结合图1可知y=与y=ax+b有两个交点,不 妨 设x1<x2。当a>0时,如图2所示,|x1|> |x2|, 即-x1>x2>0,此 时x1+x2<0,y2=>=-y1,即y1+y2>0;同理由图形经过推理可得,当a<0时x1+x2>0,y1+y2<0。答案为B。
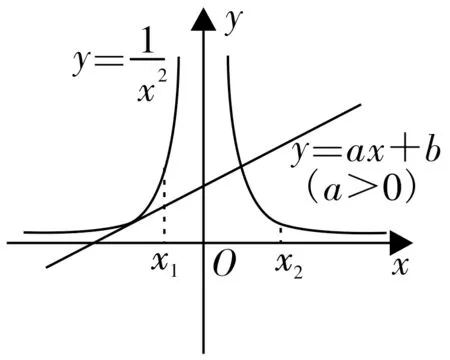
图2
解法三:由y=f(x)的图像与y=g(x)图像有且仅有两个不同的公共点,得ax2+bx,所以关于ax3+bx2-1=0(a≠0)有两个不同的解,即三次方程有两重根。不妨设重根为x1,则有ax3+bx2-1=a(xx1)2(x-x2) = 0, 从 而 有即所以当a>0时,x2>0,则x1+x2<0,y1+y2=;当a<0时,x2<0,则x1+x2>0,y1+y2=。答案为B。

