数形结合思想在高中数学解题中的应用探析
2020-02-12 09:22郭文静
中学生数理化(高中版.高考理化) 2020年1期
■郭文静
同学们在进行解题时,要合理应用数形结合方法,一方面可以改变数学解题枯燥无聊的状况,另一方面也能调动大家的积极性,更加高效率地实现数学解题。
一、数形结合思想在方程问题中的应用
在处理方程问题时,应用数形结合方法的关键是将方程运算符号两侧看成函数,先将相应的函数图像画出来,然后借助图像与坐标轴之间的关系解决方程问题。
例如:存在函数g(x)=kx,f(x)=,如果方程g(x)=f(x)有两个不同的实根,问实数k的取值范围。
分析:根据题目信息,先在坐标系中分别画出函数g(x)、f(x)的图像,然后观察两个图像的公共点,如图1 所示,直 线l1:y=,l2:y=x时,符合题目给出的条件,因此可以判断出实数k的取值范围为。
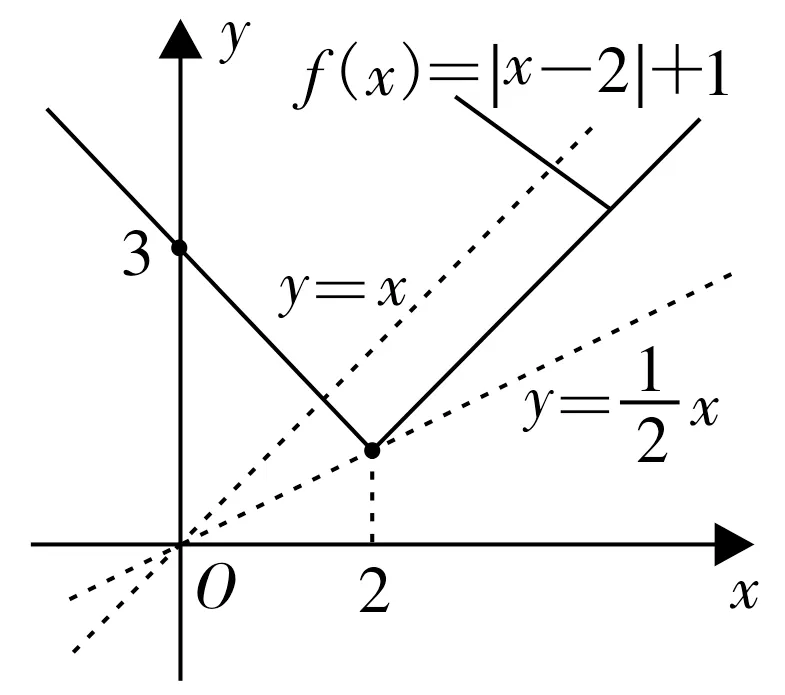
图1
二、数形结合方法在三角函数问题的应用
数形结合方法在三角函数问题中也有广泛的应用,能方便大家了解三角函数的相关概念和公式,还能帮助大家对三角函数的奇偶性、定义域和区间等相关知识进行很好的掌握。
分析:将分解成两个函数式,可将题目中的方程巧妙地转变成两个函数图像的交点。如图2所示,因为|sinx|≤1,所以在对题目进行解答的时候,单纯地考虑满足

图2
三、数形结合方法在函数极值问题中的应用
对于一些复杂的函数,同学们可以通过数形结合的方法,尝试用图形将函数画出来,借助形象的图形来求解函数极值。
例如:已知x2+y2+2x=0,求函数f=(x-1)2+(y+1)2的最小值。
分析:将图像在直角坐标系中展现出来,如图3所示,这样函数的极值问题就会转变成图像问题,可以很轻松地从图形中得出答案。
总而言之,在高中数学解题中,数形结合思想是一种十分重要的解题方法,可以显著改善同学们在解题中的复杂运算、推理,调动同学们解题的积极性,提高同学们的解题效率。因此,在实践中,大家要培养良好的数形结合思维,通过数形结合的方式解决更多的数学难题。
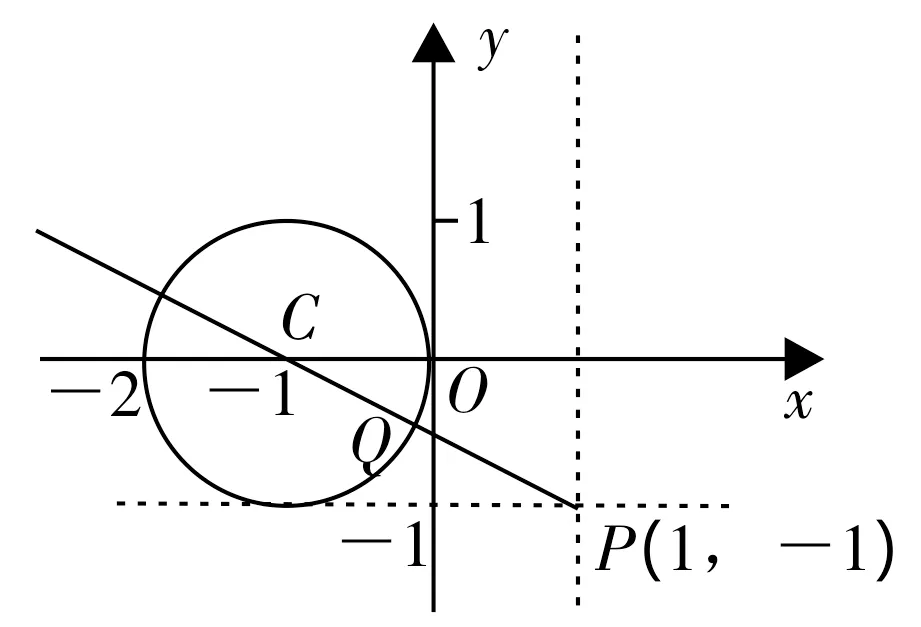
图3
猜你喜欢
中学生数理化(高中版.高考数学)(2022年4期)2022-05-25
理科爱好者(教育教学版)(2022年1期)2022-04-14
数学学习与研究(2020年16期)2020-12-28
语数外学习·高中版中旬(2020年5期)2020-09-10
语数外学习·高中版中旬(2020年10期)2020-09-10
智富时代(2019年7期)2019-08-16
智富时代(2019年7期)2019-08-16
数学学习与研究(2018年14期)2018-10-29
中学教学参考·理科版(2017年8期)2018-02-24
广西教育·B版(2017年1期)2017-05-03

