精准画图方能准确答题

■高业杰

在几何题的解答过程中，一般都需要画“草图”来帮助审题、理解题意和分析数量关系，使繁杂的题设变得清晰，抽象的问题变得直观，从而轻松地解决实际问题。然而很多时候，学生因为“草图”画得太随意，导致解答不准确。下面通过一个实例，来谈一谈画好“草图”的重要性。

一、试题呈现

二、学生答题情况

图1

学生1：如图1，因为四边形ABCD是平行四边形，所以∠B= ∠D，AB=CD，AD=BC。又因为AE⊥CD，AF⊥BC，所以∠AED=∠AFB=90°，△ADE∽△ABF，。因为AD+CD+BC+AB=28，即AD+AB=14，所以AD=6，AB=8，在Rt△ADE和Rt△ABF中，DE=所以CE=CD-DE=8-，CF=BC-BF=。

学生2：这道题需要分类讨论，应该还有一种情况，就是高AE和AF在平行四边形的外部。因为这种情况的图还没画出来，暂时得不出答案。

经过学生2 的提醒，我们知道本题应该分为两种情况，高在平行四边形外部的情况我们待会再研究，我们先来看看学生1 给出的思路是否准确，有没有不同的观点?

甚至可以得出结论：平行四边形两边之比与两边边上的高之比正好相反。到此，再来看一看学生3的结果和学生1的结果是不是一样。学生3 的思路很好，遇到与高相关的问题能想到用“等积法”，这一方法值得借鉴，但是还有其他学生给出了其他解法。

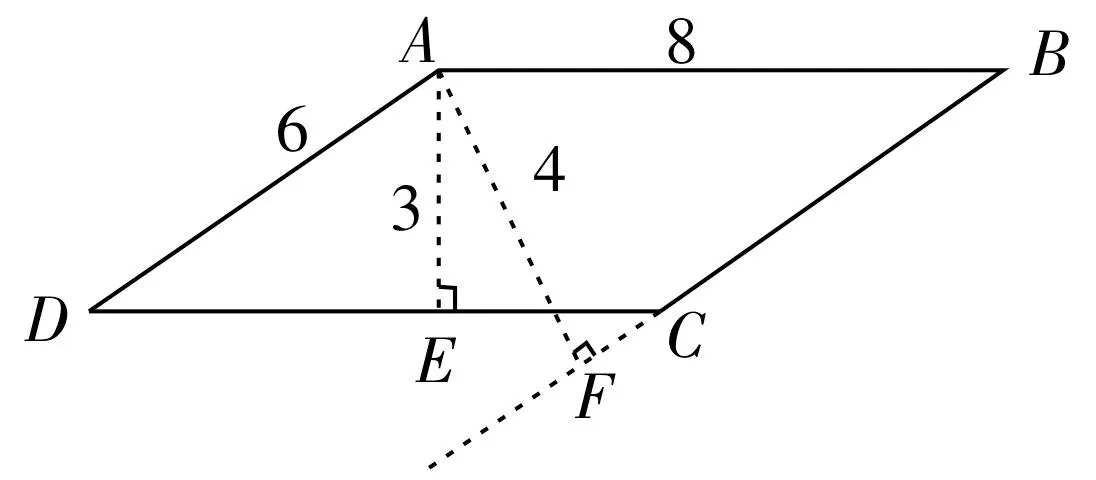
图2

学生4：学生1和学生3的思路很好，求平行四边形两边长的方法不同，但各有千秋，只是最终的答案并不准确。因为点F不在边BC上，而在BC的延长线上，如图2。所以CF=BF-BE=，因此CE-CF=。

那么为什么点F在BC的延长线上?

学生4：BC=6，BF=，由于6，即BF＞BC，因此点F在BC的延长线上。或者在Rt△ABF中，直角边AF=4，斜边AB=8，容易想到∠ABC=30°，之后准确画出图形(按条件：AD=6，AB=8，∠ABC=30°)，点F自然在BC的延长线上。

由此我们看出学生4 的分析很有道理，考虑问题非常细致，看来学生1和学生3 的解答是错误的，主要是因为画图时过于随意，所以我们在画图辅助解题时一定要尽可能地考虑到题目已知条件对图形的限制。

在之前获取的知识的基础上，我们来画图解决学生2提出的“高在平行四边形外部”这种情况。

图3

学生5：如图3所示，因为CE=CD+DE=，CF=BC+BF=，所以CECF=。综上可得，CE-CF=。

画这种情况的图形时，可先思考出在平行四边形外部的高AF是它所在直角三角形的斜边AB的一半，因此∠ABC的外角应该是30°，所以画图时应使ABCD中的∠ABC=150°。