多级立式泵动力吸振器设计与分析

陈玉球

（湖南有色金属职业技术学院，湖南 株洲412006）

0 引 言

水泵机组的运行状态可以通过振动判断，因而振动也是评价水泵的重要指标。当振动过大时，不仅会造成连接件或紧固件的松脱，甚至引起基础的裂纹，而起会引起泵组管路系统的共振，从而造成机毁人亡[1]。本文以某七级立式泵为研究对象，针对其底座振动过大的问题，涉及了振动吸振器，以期有效抑制振动。

1 动力吸振器设计计算

图1 水泵机组简图

1.1 水泵机组参数

本文分析的水泵机组参数如下：三相异步电动机功率为20 kW，质量为80 kg，泵体质量为200 kg，扬程为120 m，流量为20 m3/h，转速为2270 r/min，弹簧隔振器的刚度为230 N/mm，阻尼比为0.07，数量4个。根据现场采集的数据，泵组在运行时基座4个角的垂向振动加速度超标，振动最大幅值对应的频率为1275 Hz。期望通过设计动力吸振器减少4个角的Z向振动。

图2 动力吸振器力学模型

1.2 动力吸振器参数计算

主系统与吸振器的位移分别用X1、X2表示，则系统的运动方程为：

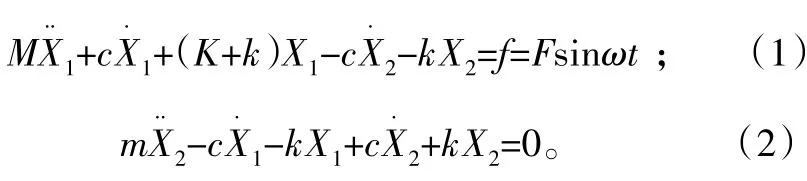
式中：M为主系统质量；K为主系统支撑刚度；m为吸振器质量；k为吸振器支撑刚度；c为吸振器阻尼系数;f为外激力，f=Fsinωt。

求解主系统、吸振器的振幅比,见式（3）、式（4）。吸振器的作用是降低主系统的振幅比[2]，将主系统的振动转移到吸振器的振动上[3]。

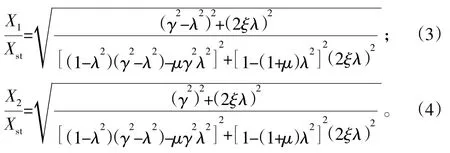
式中：Xst为主系统静变形；μ为质量比,μ=m/M，一般取0.01～0.1；ξ为阻尼比λ为强迫振动与主系统固有频率之比；γ为吸振器固有频率与主系统固有频率之比；f为外激力，f=Fsinωt。

根据最优同调及最优阻尼条件，可以推导出动力吸振器的支撑刚度和阻尼系数[4]：

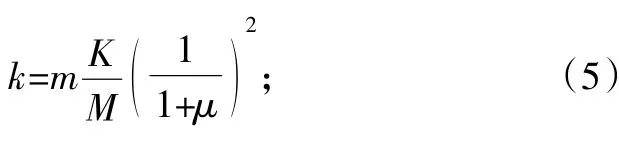
由此，吸振器的设计参数可以全部计算完成。

根据计算结果并按照吸振器的设计公式，绘制不同质量比下主系统及吸振器的响应曲线[5]，如图3所示。当质量比为0.15时，吸振器的作用频率范围最广、可以满足较多频率下的减振要求，因此初步决定采用质量比为0.1。

图3 不同质量比下的响应曲线

2.3 动力吸振器设计与建模

对未施加动力吸振器的泵组模型进行模态分析，根据模态分析结果及已知条件判断发生共振的模态阶数[6]。同时，对泵组进行谐响应分析，根据幅频曲线求出共振模态下的动刚度和模态质量[7]。

第18阶固有频率接近，初步判断是外激励引发第18阶模态，从而结构产生共振。因第18阶频率对振动的贡献最大，因此设计动力吸振器降低第18阶频率附近的振幅。根据谐响应分析计算动刚度及模态质量即动刚度[8]为k=1.50×108N/m，模态质量m′=22.9 kg。此时吸振器的设计参数如下：m=2.29 kg，f固=1287 Hz，k=1.50×108N/m，阻尼比ξ=0.06。

表1 前二十阶固有频率

3 动力吸振器减振效果分析

分别对为含有动力吸振器和含有动力吸振器的泵组进行谐响应分析[9]，在 基 座上施加幅值为2000 N 的简 谐 力[10]，设置频率分析范 围0 ～3000 Hz。分析结果如图6～图8所示。结果表明,该动力吸振器能够有效降低1280 Hz附近的振动，表明吸振器设计合理，达到了减振效果。

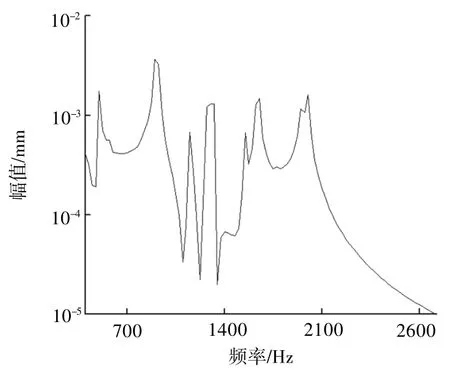
图4 Z方向谐响应分析幅频曲线

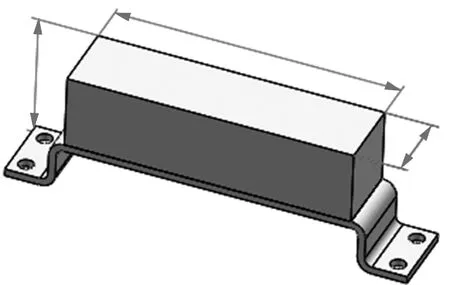
图5 吸振器模型

图6 X向幅频曲线

4 结 论

本文针对某多级立式泵进行了动力吸振器设计，并得出了如下结论：1）对不同质量比下的动力吸振器模型进行振动响应分析，质量比越大,则振幅降低越明显,且减振的频率范围越广；2）根据已知条件及仿真分析，判定第18 阶模态共振是引发泵组振动的主要频率；3）针对第18阶频率设计了动力吸振器并进行了减振效果分析，结果表明吸振器能够有效地降低泵体的振动，设计合理。

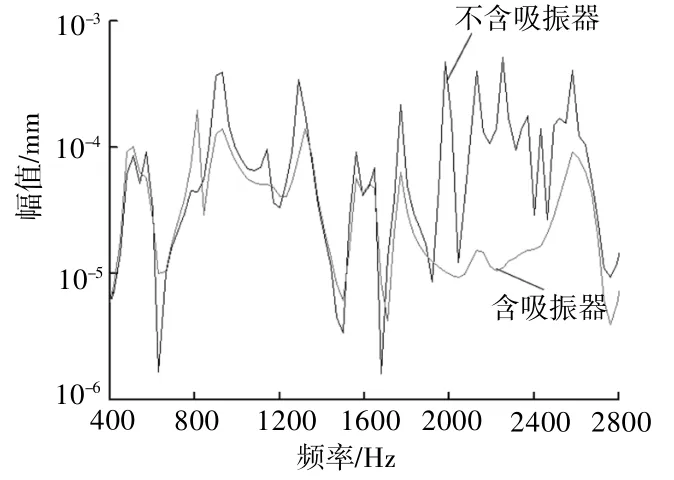
图7 Y向幅频曲线

图8 Z向幅频曲线