实系数多项式因式分解的一种矩阵初等变换法
张 楠,梅月兰,王 双*
(1.盐城师范学院 数学与统计学院,江苏 盐城 224002;2.昆明理工大学 城市学院,云南 昆明 650051)

本文运用矩阵的初等变换法讨论实系数多项式在实数域内的因式分解问题,建立有重因式的实系数多项式在实数域内的因式分解新方法,以将已有的关于整系数域内的多项式因式分解的相关结果推广到实系数域.
1 初等变换的基本内容
定义称一个以R[x]中的多项式为元素的矩阵为x-矩阵,并称x-矩阵的以下3种变换为初等变换:①矩阵的两行互换位置;②矩阵的某一行乘以一个非零常数;③矩阵的某一行的φ(x)倍加到另一行,其中φ(x)是R[x]中的一个多项式[5].
2 主要结果
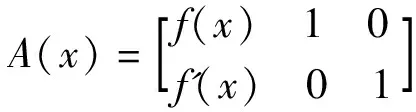
进一步,d(x)是f(x)与f'(x)的最大公因式,且满足d(x)=u(x)f(x)+v(x)f'(x).
证明由于f(x)存在重因式,则f(x)与f'(x)均不为零.显然f'(x)必为二者中次数较低的多项式,于是将f'(x)乘以一个适当的多项式可以消去f(x)的最高项,此时矩阵A(x)的第1列变为r1(x)与f'(x),存在q1(x)满足
f(x)=f'(x)q1(x)+r1(x).
若r1(x)=0,则d(x)=cf'(x),其中cR.若r1(x)≠0,则重复上述过程.由于f(x)与f'(x)的次数有限,经过有限次初等行变换,必然出现矩阵的第1列仅有1个非零元素F(x),而其他元素均为零,则d(x)=cF(x).
上述过程用矩阵初等行变换可表示为


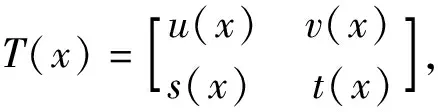
由A(x)经过初等行变换得到B(x),使T(x)A(x)=B(x),T(x)可逆,那么A(x)=T-1(x)B(x),便有f(x)=d(x)u1(x),f'(x)=d(x)s1(x),于是d(x)是f(x)与f'(x)的公因式.
又因为T(x)A(x)=B(x),便有d(x)=u(x)f(x)+v(x)f'(x).设h(x)是f(x),f'(x)的任意公因式,因为h(x)|f(x),h(x)|f'(x),所以h(x)一定整除它们的组合u(x)f(x)+v(x)f'(x)=d(x),即h(x)|d(x).
于是d(x)可被f(x)与f'(x)的任一公因式整除,故d(x)是f(x)与f'(x)的最大公因式.证毕.
由定理1可知,若f(x)存在重因式,则d(x)必为f(x)的一个因式,即存在g(x),使得f(x)=d(x)g(x).若d(x),g(x)均有重因式,则可重复上述矩阵初等变换的方法,分别求得d(x),g(x)的因式,依次可对f(x)进行因式分解.
3 举例说明
运用矩阵的初等变换法对以下3个含有重因式的多项式进行因式分解.


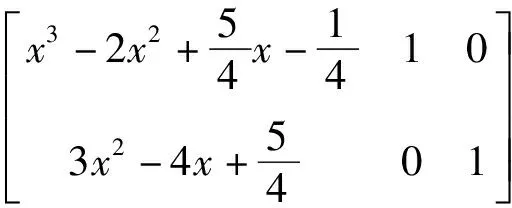

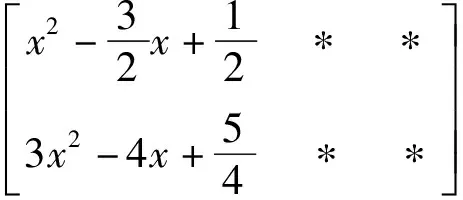
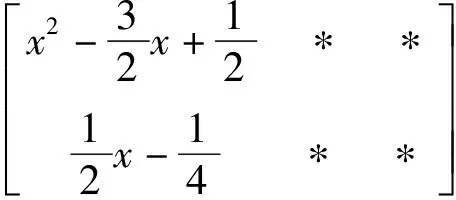

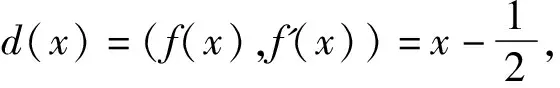
则:f(x)=d(x)q(x)
例2 求多项式f(x)=x4-4x3+6x2-4x+1在实数域的因式分解式.
解先求得f(x)的导数f'(x)=4x3-12x2+12x-4,利用矩阵初等行变换方法可得:
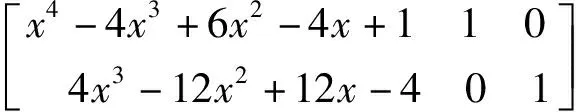
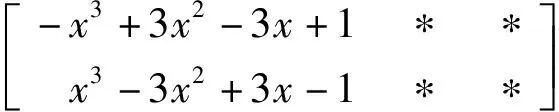
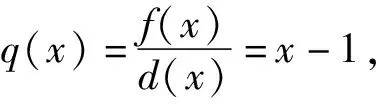
类似地,可将x3-3x2+3x-1分解为(x-1)3,从而f(x)=(x-1)4.
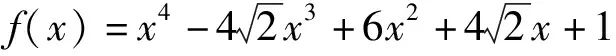
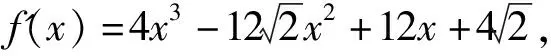
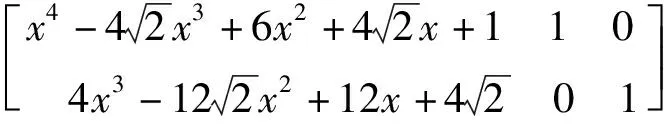


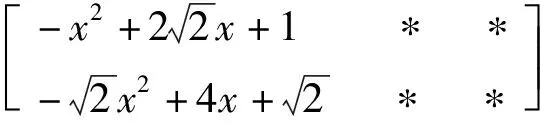
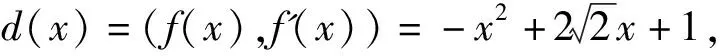

注:本题直接运用了矩阵的初等变换法对高次多项式进行分解因式,按照固定的步骤可简单明了地得到多项式的一个因式.若解题过程中不能直接看出的因式,可以继续重复上述步骤对d(x)进行因式分解.
4 结束语
利用矩阵的初等变换法,可以对存在重因式的实系数多项式在实数域进行因式分解,并将已有的关于整系数域内的多项式因式分解的相关结果推广到实系数域.使用该方法的前提是所分解的多项式存在重因式,即可通过矩阵初等变换法求多项式及其导数的最大公因式,从而得到多项式的一个因式.该方法可以在很大程度上简化繁杂的计算过程.

