弯扭组合实验的理论分析与验证
闵 磊
(新疆大学 机械工程学院,新疆 乌鲁木齐830049)
0 引言
基于新疆大学机械工程学院力学实验室的BWN-1型弯扭组合实验装置,针对仪器使用说明书所给出的-45°-0°-45°应变花的贴片方式与《材料力学》和《工程实验力学》教材上所给出的0°-45°-90°应变花贴片方式的不同之处,采用坐标变换应力法与平面应变分析法2种分析方法对主应力实验的原理进行理论分析和实验验证,以对弯扭组合实验的顺利开展提供理论指导[1-4]。
1 坐标变换应力法的理论分析
BWN-1型弯扭组合实验装置主要用于测量弯扭组合受力下薄壁圆管表面上某一点的主应力大小和方向。选用铝合金薄壁圆管进行主应力实验,铝合金圆管的左端固定在实验支架上,右端安装一个施加弯扭组合受力的扇臂,扇臂的半径即为扭转力臂,铝管上粘贴应变花的截面到扇臂的距离即为弯曲力臂。铝合金材料的弹性模量E=71 GPa;泊松比μ=0.32;铝管的外径D=40 mm;内径d=34 mm;弯曲力臂L=230 mm;扭转力臂R=200 mm;抗弯截面系数Wz=πD3(1-a4)/32;抗扭截面系数Wp=πD3(1-a4)/16,其中a=d/D为铝管的内外径之比。
按照增量法加载实验做分析计算,每次加载增量ΔFp=70 N,计算应变花粘贴位置横截面上作用的弯矩和扭矩。其中,弯矩Mz=ΔFp×L;扭矩Mx=ΔFp×R。
选取坐标系(x,y)为参考系,铝管轴线0°方向为x轴,垂直于铝管轴线90°方向为y轴,构成原始平面应力单元体。将原始应力单元体向顺时针方向旋转,与x轴成顺时针-45°方向为x1轴,与x轴成逆时针45°方向为y1轴,构成新坐标系的应力单元体。坐标参考系示意图如图1所示。

图1 坐标参考系示意图
1.1 平面应力单元体分析
实验装置粘贴应变花处平面应力单元体中的原始应力主要包括:沿着x轴方向的最大弯曲正应力σx;沿着铝管横截面边缘处切线方向的扭转最大切应力τxy;沿着y轴方向的正应力σy。计算结果如下:
(1)
1.2 斜截面应力分析
将公式(1)的计算结果代入斜截面应力公式(2)和公式(3),分别计算出斜截面单元体x1轴和y1轴方向的正应力和切应力。计算结果如下:
(2)
(3)
1.3 广义胡克定律分析实验应力
通过广义胡克定律公式(4)可以推导得到应力计算公式(5)[3,5]:
(4)
(5)
在-45°-0°-45°坐标系(x1,y1)中0°方向应变实际是45°方向的应变,(-45°)对应于x轴,45°对应于y轴;将相应的应变符号代入平面应变分析公式(6)中,解得结果见公式(7):
(6)
解得:
(7)
1.4 平面实验主应力分析
根据应力值σx=σ-45°,σy=σ45°,τxy=τ-45°,把公式(5)和(7)的结果代入主应力计算推导出公式(8)和(9),求解主应力的大小和主方向角。其中,主方向的0°位置轴线与铝管的轴线成-45°,即x1轴方向。
(8)
(9)
2 平面应变分析法的理论分析
选取初始应力状态单元体的坐标系不变,即轴线0°方向为x轴,垂直于轴线的90°方向为y轴,应用平面应变状态下的应变公式写出如下方程[3,5]:
(10)
联立方程解得:
(11)
主应变的大小和主方向角计算公式为:
(12)
(13)
2.1 主应变和主方向的实验值
将公式(11)代入公式(12)和(13),化简得主应变计算公式(14)和主方向角计算公式(15):
(14)
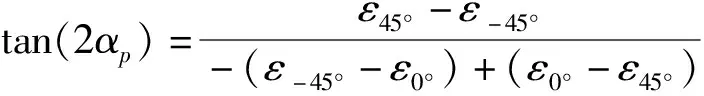
(15)
主方向的0°位置轴线在铝管的轴线方向,即0°的x轴方向。
2.2 主应力的实验值
平面应力状态的σ2=0,将公式(14)代入广义胡克定律公式(16):
(16)
即可推导出主应力计算公式为:
(17)
显然,2种分析方法得到的主应力公式(8)和(17)完全相同,主应力的主方向角计算公式(9)和(15)不相同。
3 实验数据的检验
3.1 主应力和主方向角的理论值
主应力的理论值[3,5]为:
(18)
主方向角的理论值为:
(19)
3.2 主应力和主方向角的实验值
通过实验测得实验数据为:
(20)
将实验数据代入公式(5),(7),(8)解得主应力的实验值为:
(21)
将实验数据代入公式(9)和(15),求解主方向角的实验值。
以-45°(x1轴线方向)为0°位置的主方向角:α'p=23.6°。
以0°(x轴线方向)为0°位置的主方向角:αp=-21.4°。
而且:αp=-45°+α'p=-21.4°,说明2种分析方法求得的主方向角完全一致。
4 应变片粘贴位置偏移对测量误差的影响
《工程实验力学》第5章第5.3节分析证明了应变片的粘贴偏差对应变测量误差的影响。取主方向与应变片粘贴位置的夹角为φ,粘贴位置角度的误差为Δφ,应变测量的绝对误差Δεφ,那么有分析结论[4]:
Δεφ=(ε1-ε3)·sin(2φ+Δφ)·sinΔφ
(22)
将实验数据代入公式(14),计算出主应变:ε1=88.54×10-6,ε3=-38.54×10-6。
-45°应变片粘贴位置的夹角φ=(-20.5°)-(-45°)=24.5°。
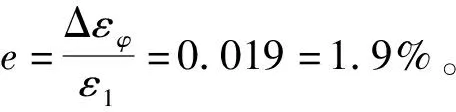
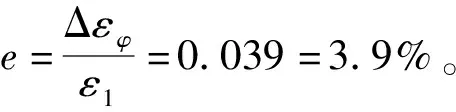
实验测量的应力值在考虑相对误差后的范围为:σ1=6.144~6.265 MPa。可见贴片误差应该小于2°。同理,计算0°和45°方向应变片的粘贴偏差误差,最后分析综合误差。
如果考虑应变片在主应变坐标轴中的相对位置,那么:
φ-45°=-24.5°,φ0°=20.5°,φ45°=65.5°。
Δφ=1°时的相对误差为:
e-45°=-1.86%,e0°=1.67%,e45°=1.86%。
Δφ=2°时的相对误差为:
e-45°=-3.66%,e0°=3.42%,e45°=3.66%。
其绝对误差为:
Δε-45°=-3.24×10-6,Δε0°=3.02×10-6,Δε45°=3.24×10-6。
分析结果表明:实验装置的贴片方式的相对误差要比0°-45°-90°的贴片方式小。主应力测量的相对误差:eσ1=-3.21%,eσ3=6.90%。
根据误差理论间接测量误差传递原理[6-7],可以推导出间接测量的系统误差与直接测量误差的传递关系计算公式。由于主应力与测量应变不满足线性规律,只能按误差的定义计算间接测量误差。不含误差的主应力用σi表示,包含有误差的主应力用σ'i表示,主应力的间接测量误差Δσi=σ'i-σi。其中:
(23)
得到:
(24)
代入数据解得主应力间接测量传递的系统误差:Δσ1=0.007 MPa,Δσ3=-0.007 MPa;因为贴片方位偏移导致间接测量误差的相对误差为:eσ1=0.116%,eσ3=-0.864%。其他误差为测力传感器、应变仪读数等系统误差和环境因素引起的误差。
5 结束语
通过理论分析与实验验证,更加清晰地明确了弯扭组合主应力实验的原理和方法。对照0°-45°-90°应变花的主应力公式,将-45°-0°-45°应变花中各对应方向的应变互换,得到的主应力公式是完全相同的。但是,将相同方法用于主方向公式,其结果却不同。这说明主方向公式不能作简单地互换修改。实验数据的误差计算结果说明在最大主应力的测量误差中因应变片粘贴方向偏移影响的误差只有0.116%,其他误差为测力传感器、应变仪、实验环境等因素引起的误差。
——以淮南矿区为例

