基于免逆牛顿法的对称张量Z-特征对可信验证

桑海风, 李 敏, 刘畔畔, 王春艳, 栾 天

(北华大学 数学与统计学院, 吉林 吉林 132013)

张量特征值问题在盲源分离理论、 磁共振成像、 高阶Markov链、 分子构象等领域应用广泛[1-3].目前, 关于张量特征值问题的研究已有许多结果[4-6].可信验证是指对于一个给定的求解问题, 构造算法并证明用该算法计算出的区间内必存在该问题的精确解[7-8].在高精度应用领域, 计算结果的可靠性至关重要, 微小计算误差的积累都可能导致重大事故[9-10].因此研究张量特征值的可信验证问题具有重要意义.本文利用免逆数值牛顿法及免逆区间牛顿法, 研究对称张量Z-特征值和特征向量的可信验证方法.首先将计算对称张量Z-特征值的公式化为等价的非线性系统, 其次基于免逆数值牛顿法及区间牛顿法理论, 提出一种计算Z-特征对的可信验证算法.该算法输出Z-特征对的一个近似解及其相应的可信区间解, 使得在可信区间解内必存在一个精确的Z-特征对.

1 预备知识

定义1[5]设A是m阶n维张量,Πm是指标为m的置换群, 如果对任意的π∈Πm, 均有ai1i2…im=aπ(i1i2…im), 则称A为对称张量.

定义2[5]设A是m阶n维张量, 如果对于实数域中的数λ, 存在一个非零向量x∈n, 使得

(1)

则称λ为张量A的一个Z-特征值,x为A的属于特征值λ的一个Z-特征向量, (λ,x)为A的一个Z-特征对.

注1Axm-1为n维向量, 其第i个元素为

为计算方便, 给出式(1)的等价非线性系统

(2)

为了用牛顿法求解非线性系统(2), 本文给出F(x,λ)的Jacobi矩阵计算格式.若A为m阶n维实对称张量, 则F(x,λ)的Jacobi矩阵JF(x,λ)为实对称矩阵, 且具有如下形式:

(3)

事实上, 本文问题的关键是说明Axm-1的Jacobi矩阵为(m-1)Axm-2, 且Axm-2为对称矩阵, 因此分两步进行.

第一步, 说明Axm-1的Jacobi矩阵为(m-1)Axm-2.因为

且A为对称张量, 则

即JAxm-1=(m-1)Axm-2.

第二步, 说明Axm-2为对称矩阵.因为

且aij…im=aji…im, 即证得Axm-2为对称矩阵.故

为对称矩阵.

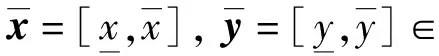
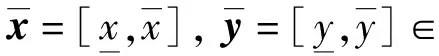
定义5[12]设映射f:n→, 若存在区间值映象n→, 使得对任意均有

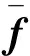
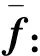
2 主要结果

Moore[13]第一次提出了区间牛顿迭代法.在每次迭代过程中, 该方法不仅得到了近似解, 同时也得到了相应的误差.区间牛顿法的这个特点, 显然一般点迭代不具备.

定义7[13]设映射f:D⊂n→n在D上连续可微,Jf(x)为f(x)的Jacobi矩阵.设(D)为D上有界区间向量的集合,是Jf(x)的具包含单调性的区间扩展, 称

即为区间牛顿迭代法.由于每一步都要计算区间矩阵的逆, 计算工作量极大, 因此该算法并不实用.Krawczyk[14]针对Moore的区间牛顿程序在计算量方面的缺陷, 对牛顿算子进行改进, 提出了一种不需要计算矩阵逆的Krawczyk算子.

定义8[14]设映射f:D⊂n→n在D上连续可微, 设是Jf(x)的具包含单调性的区间扩展, 称

为Krawczyk算子, 其中Y为任意n×n阶非奇异矩阵.

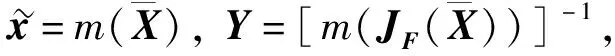
(4)

(5)

其中k=0,1,2,….

Moore[15]对Krawczyk区间牛顿迭代法提出了存在收敛性定理.

定理1[15]设映射f:D⊂n→n在D上连续可微,是Jf(x)的具包含单调性的区间扩展.若初始区间向量是一个n维立方体, 算法由式(5)定义, 相应的满足则有如下结论:

2)对任意k∈, 有且

Rump[16]改进了区间牛顿法, 使其更便于实际应用.

定理2[16]设映射f:D⊂n→n在D上连续可微.给定向量n、 区间向量n以及矩阵T∈n×n, 其中且给定区间矩阵n×n满足如果区间判定条件

基于上述理论, 本文提出对称张量Z-特征对的可信验证算法.

算法1可信验证算法.

输入: 对称张量A, 初始值x0∈n,λ0∈,k=0, 数值容差ε和最大迭代次数N;

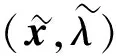
步骤1)求解

得(Δxk,Δλk), 其中F(xk,λk)和JF(xk,λk)分别由式(2)和式(3)给出.

步骤2)若k≤N, 则执行步骤3), 否则返回“失败”, 算法终止.

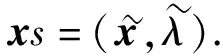
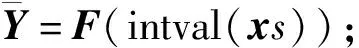
② 计算JF(xs)的近似逆矩阵T;

④ 令iter=0.

若iter≤15, 则执行下述步骤, 否则返回“失败”, 算法终止;

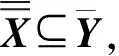
由定理2可得下述命题.

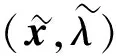
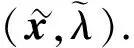
3 数值算例

下列数值实验基于Windows 7操作系统(Intel Core 2.30 GHz, i3-2350M CPU, 4.00 GB RAM), 软件是MATLAB R2011a(INTLAB V6).选择文献[1]中给出的4阶3维对称张量A, 其元素取值如下:

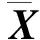
由表1可见, 算法1能有效求解出张量的特征对及其可信区间.

表1 算法1的计算结果