网孔阻尼型水润滑艉轴承减振特性
金勇, 邓天扬, 欧阳武, 刘正林, 劳坤胜, 何涛
(1. 武汉理工大学 高性能船舶技术教育部重点实验室,湖北 武汉 430063; 2.国家水运安全工程技术研究中心可靠性工程研究所,湖北 武汉 430063: 3.武汉第二船舶设计研究所,湖北 武汉 430064)
舰船在航行过程中由于推进轴系安装以及配合件摩擦等原因会产生各种振动和噪声,对舰船的声隐性、可靠性以及乘员的舒适性影响巨大。由于螺旋桨的悬伸布置,尾轴承的工作条件极其恶劣,且由于轴承是轴系振动向外界传递振动能量所遇到的首个隔振元件,因此,响应幅值相对较大的尾轴承减振降噪研究对船舶推进轴系的振动理论体系完善,对提高诸如水下航行器等舰船的静音水平和生存能力都具有重要意义。
近年来,在高速铁路车厢材料、高速混凝路面、阻尼器、泡沫金属材料、空气静压轴承、油润滑轴承等领域,利用多孔结构提高材料减振降噪性能都有一些工程案例[1-5],而水润滑艉轴承方面的工程应用案例还未见报道。本文将多孔结构引入水润滑艉轴承设计,在橡胶板条材料基础上,研究网孔结构的动力学行为,揭示多孔结构减振的机理及影响因素。
钟坤[6]建立了混凝土材料的多孔结构几何模型以及由微细孔腔混叠构成的吸声模型,并通过仿真计算分析得到:1)影响路基减振降噪水平的主要因素为模型的材料孔隙率、厚度和骨料直径等,2)孔隙率和骨料直径是主要影响因素。刘悬竹[7]建立了一种微穿孔阻尼减振结构,并利用有限元分析软件对比分析了有无微孔情况下的模态特性,结果表明微孔结构减振效果良好。Okada等[4]研究了一种电刷,电刷基体材料为铜-石墨,创新设计体现在基体为网孔结构,通过仿真与试验证实了这种结构对滑动摩擦诱发的振动具备一定的衰减能力,同时也能降低摩擦系数、磨损率以及接触电压。Shan等[8]研究了多孔结构在高速卧式加工中心立柱上的应用,利用Abaqus分析了有无孔条件下的静态、动态结构特性,得出多孔立柱可以节约材料,降低结构质量,改善加工中心的速度特性。Qin等[9]研究了带有多孔结构的声振传感器,利用Ansys进行了低阶模态分析,并进行了基于应变的结构优化研究,得出多孔结构虽然应力变化较大,但共振频率变化较小。
本文以舰船水润滑橡胶尾轴承为研究对象,应用Ansys有限元分析工具对其进行模态和谐响应分析,并通过振动试验分析网孔对其振动响应的影响规律。
1 有限元模型
尾轴承在实际运转过程中,由于螺旋桨的悬臂载荷,其主要承载区集中在轴承的下半区,因此,在轴承下半区的板条上开设轴向穿孔对轴承的影响最大,故而本文仅分析底部网孔设计下的静动特性。
尾轴承截面结构如图1所示,其中(a)为普通尾轴承,(b)为网孔阻尼型尾轴承,2种轴承的结构参数如表1所示,材料参数如表2所示。衬套的材料选用常规的碳钢,而轴瓦板条则选择较软的丁腈橡胶。

图1 尾轴承结构截面Fig.1 Structure sectional view of stern bearing
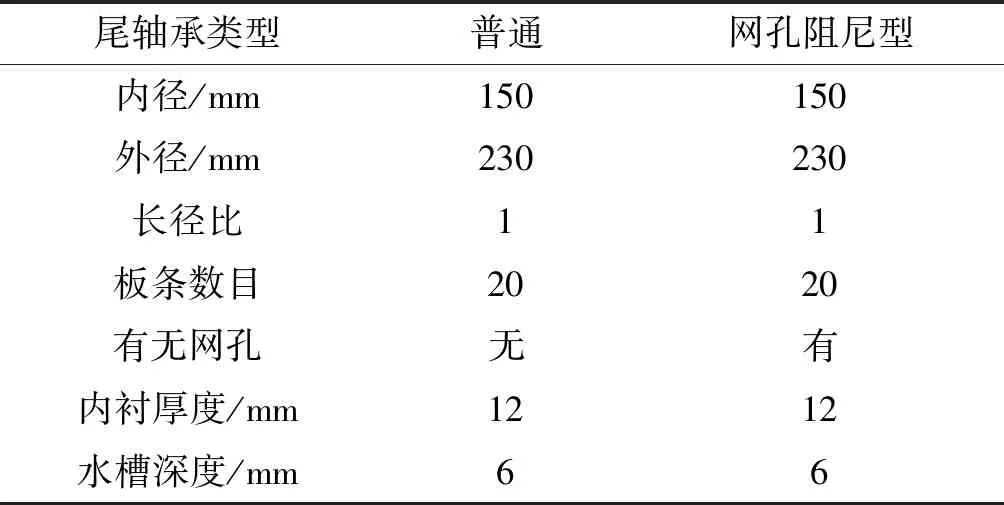
表1 尾轴承结构参数Table 1 Structure parameters ofstern bearing

表2 尾轴承材料参数Table 2 Material parameters ofstern bearing
将表2定义材料属性赋予尾轴承的不同结构,并采用以六面体主导的多域法和同样的网格尺寸对艉轴承进行网格划分,生成的有限元模型如图2所示。2种类型的尾轴承在网格单元和网格节点数量上差异不大,网格单元数量在8万左右,网格节点数量在4万左右。

图2 尾轴承有限元模型Fig.2 Finite element model diagram of stern bearing
2 网孔直径对尾轴承模态的影响
2.1 分析设置
2类尾轴承的轴瓦板条和金属衬套之间的接触类型都设置为固紧(BONDED),这是因为水润滑橡胶尾轴承的轴瓦板条是硫化在衬套上的,两者之间不能相对运动。
很多振动控制的工程案例已经得出[10-11],结构的振动响应取决于外激励和结构的模态,舰船轴系在运转过程中所受到的外激励一般频率都不高,因此,结构的高阶模态对振动响应的影响较小,且在阻尼条件下衰减较快,另外,高阶振动对应的外激励能量一般较弱,不易激发出来[12],而结构的低阶模态由于接近外激励频带,易出现共振,对振动响应的影响最大,故舰船工程领域的结构振动分析基本只考虑中低频段的模态。
2.2 自由模态
提取前20阶普通尾轴承和网孔直径分别为1、2、3、4 mm的阻尼型轴承的自由模态分析结果,作对比分析曲线图,如图3所示,图中忽略了前6个固有频率为零的刚体模态,并前移了后续的模态,即图中的第1阶有效模态实际是模态分析结果中的第7阶模态。

图3 尾轴承自由模态随网孔直径的变化曲线Fig.3 Free mode of stern bearing with different mesh diameters
从变化曲线图上可以看到,自由模态条件下,各型尾轴承的固有频率与模态阶数的变化趋势基本是一致的,都呈现渐次递增的形态。另外,与无网孔的普通尾轴承相比,网孔阻尼型各阶固有频率的数值都有不同程度的降低,且随着网孔直径的加大,降低的程度越大。其中,孔径为2 mm和3 mm时,固有频率的降低程度相差不大,而孔径增大到4 mm时,各阶固有频率的数值降幅较大,特别是在前3阶的变化梯度较大,降幅尤为明显。这说明尾轴承底部承载区的轴向网孔设计在一定程度会改变结构的静态特性,在降低模型质量的同时也减小了结构的静刚度,因此,固有频率会降低。
2.3 约束模态
尾轴承一般被固定安装在轴系的轴承座中,轴承衬套的旋转、平移等自由度均被限制,据此,本文在模型的衬套外圆柱面施加了一个固定约束(FIXED SUPPORT)。
提取前20阶普通尾轴承和网孔直径分别为1、2、3、4 mm的阻尼型轴承的约束模态分析结果,作对比分析曲线图,如图4所示,由于模型的6个自由度均被限制,而模态与系统自由度密切相关,某个方向被约束,则该方向下的刚体模态就会消失,故约束条件下的模态分析结果中前6个模态均不为零,都是有效模态。另外,对比图3和图4可以得出,约束条件下,各阶固有频率随阶数增大的趋势与自由条件下一致,但在数值上大于对应的自由模态频率,这是因为当模型某个方向被约束时,则等效于在该方向增加了刚度而间接增大了结构的固有频率。

图4 尾轴承约束模态随网孔直径的变化曲线Fig.4 Constrained mode of stern bearing with different mesh diameters
3 网孔直径对尾轴承谐响应特性的影响
尾轴承的谐响应特性分析就是在尾轴承结构上施加简谐激励外载荷,并基于模态分析结果研究结构的稳态响应。前述模态分析已经得到了网孔阻尼型和普通尾轴承的前20阶固有频率,在此基础上对两种结构进行谐响应分析就可以得出网孔直径对尾轴承谐响应特性的影响规律和水平,为后续网孔阻尼型尾轴承的工程应用与优化设计提供数据基础。
谐响应分析采用的有限元模型与模态分析时相同,边界条件设置与约束模态分析时一致,载荷为简谐正弦谱激励,即P=Asin(ωt),根据试验工况,设定激励力的幅值A为0.2 MPa,并根据尾轴承模态分析的结果,设定激励初始频率为400 Hz,截止频率为850 Hz,在分析设置中设定分析子步的频率间隔为5 Hz。
通过比较特征点的频率-位移图可以直观的分析结构的谐响应特性,因此,在2种轴承的相同位置,如图5所示的节点1,提取频率-位移图可以比较有无网孔对谐响应特性的影响,另外,在网孔阻尼型尾轴承的网孔位置,如图5 (b)所示的节点2、3,提取频率-位移图则可以分析网孔对谐波传递路线的影响。
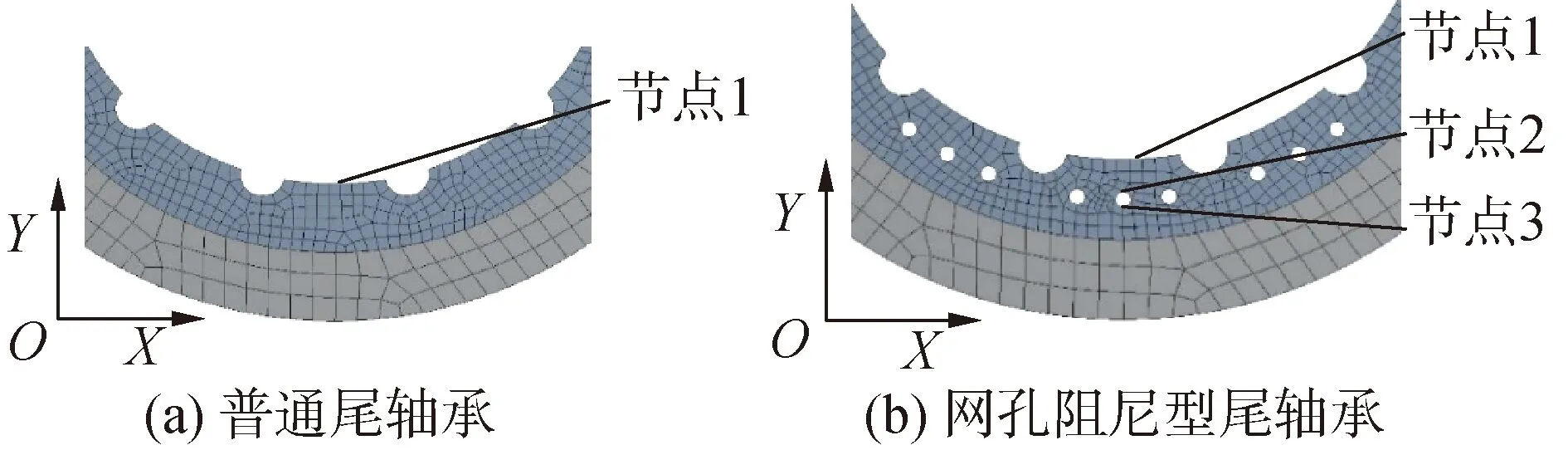
图5 提取节点位置Fig.5 Location of the fetch node
由模态分析得出轴承内衬主要表现为弯曲模态,且最大变形区域集中在板条的两端,因此,各不同网孔直径的尾轴承谐响应分析皆提取节点1的垂向(Y)数据进行对比分析,其结果如图6所示。

图6 尾轴承节点1频率-位移响应曲线Fig.6 Frequency-displacement response diagram of fetch node 1#
由节点1的频率-位移响应图可以看出,在分析频带内的635 Hz和690 Hz处,各型尾轴承都有2个突出的谐波响应分量,其他频率成分的幅值基本可以忽略。另外,局部放大635 Hz处的谱峰也可以看到,无网孔的普通尾轴承响应位移量最大,达到8.478 mm,增设网孔后尾轴承位移量逐渐降低,在孔径为4 mm时降低程度尤为明显,只出现了微弱的数值,为0.193 mm,降幅接近98%。这就可以说明尾轴承底部板条的网孔设计的确可以降低轴承的位移响应,且随着网孔直径的增大,对谐波激励的衰减能力就越高。
为了更明确地验证网孔在谐波传递路线上的衰减作用,选择减振效果最好的4 mm网孔直径的阻尼型尾轴承进行深入分析。首先选择图5 (b) 所示的轴承底部网孔上下2个节点,提取节点的垂直方向(Y向)的谐响应频率-位移响应图,对比分析结果如图7所示。
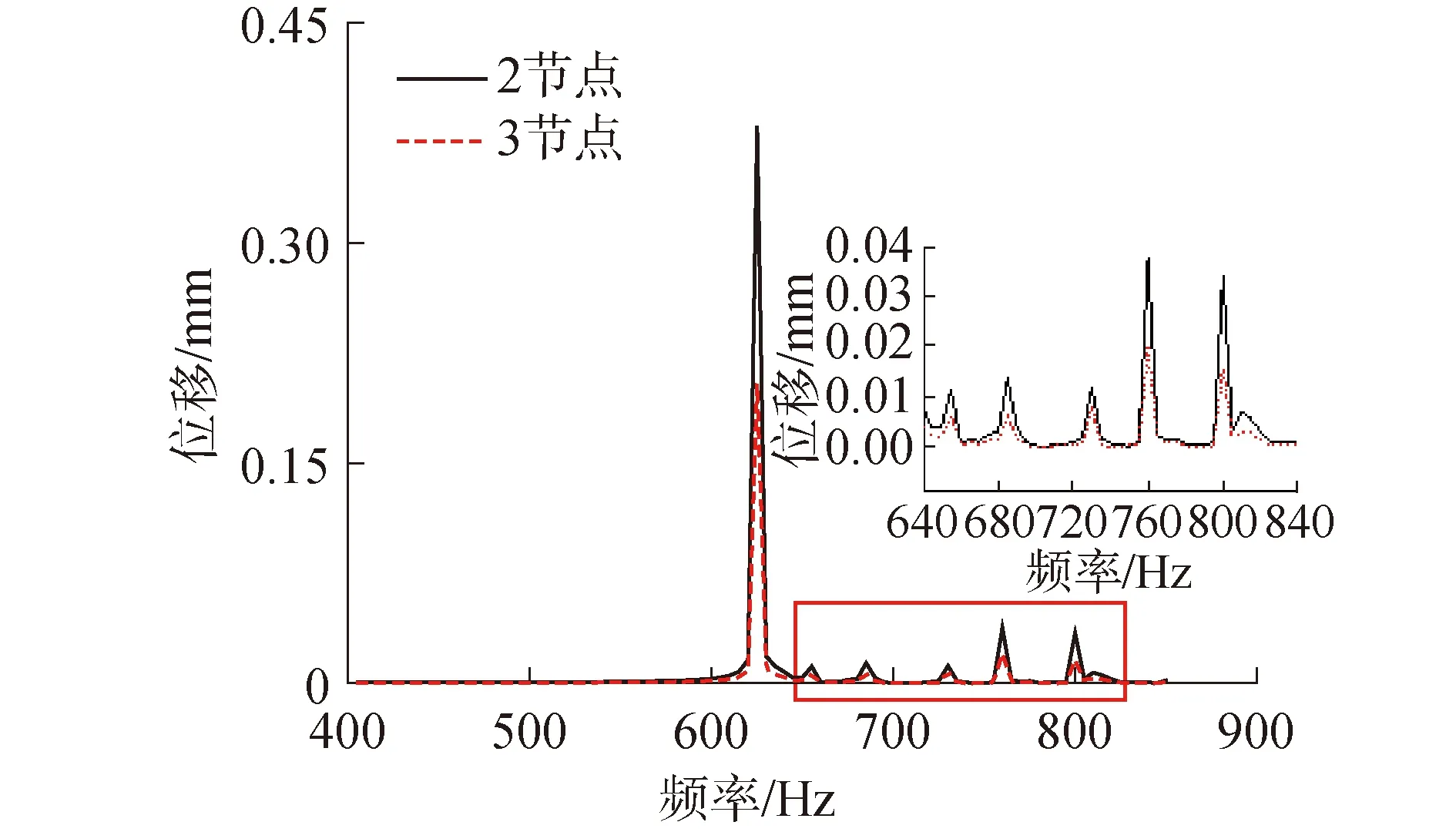
图7 网孔阻尼型尾轴承节点2、3频率-位移响应曲线Fig.7 Frequency-displacement response diagram of fetch node 2#,3# on mesh damping type stern bearing
从对比结果图中可以发现,在整个分析频带内,网孔上方节点的位移响应幅值都大于下方节点,在频率625、655、685、730、760、800 Hz处出现的几个谱峰处更加明显。如频率625 Hz处,网孔上方节点2处的响应位移幅值为0.380 mm,下方节点3处的响应位移幅值为0.204 mm,降幅超过46%。这说明谐波激励经过网孔的传递后,响应幅值有了很大的衰减。
通过模态及谐响应分析可以得出在水润滑橡胶尾轴承底部板条上开设轴向网孔可以有效降低外激励下的振动响应位移幅值。对这种网孔阻尼型尾轴承的减振机理可以采用如图8所示的分析过程。

图8 网孔阻尼型尾轴承减振机理Fig.8 Damping mechanism of mesh damping type stern bearing
从图8可以得出,轴系工作时产生的振动传递到尾轴承时,振动能量都会被板条阻尼衰减掉一部分,但当振动能量从网孔阻尼型尾轴承传递时,网孔又会消耗掉一部分,能够穿出内衬板条的振动能量会更少。更直观的表现如图9所示,图中纵坐标y代表结构受到激励后的振幅,横坐标t代表响应时间,当2种尾轴承受到同样的初始激励,网孔阻尼型尾轴承的振幅更低,衰减时间更短。

图9 2种尾轴承振幅-时间关系曲线Fig.9 The amplitude-time relationship graph of two kinds of stern bearing
4 网孔阻尼型水润滑橡胶尾轴承试验分析
对普通尾轴承和孔径为4 mm的阻尼型尾轴承进行振动试验,研究对比2种尾轴承的振动响应随载荷和轴转速的变化情况,为水润滑艉轴承的减振设计研究提供基础试验数据。普通尾轴承和网孔阻尼型尾轴承的实物图如图10所示,试验机如图11所示。

图10 2种尾轴承实物图Fig.10 Two kinds of stern bearing

图11 SSB-100型船舶尾轴试验机Fig.11 SSB-100 ship stern shaft testing machine
在试验条件下,环境振动对2种尾轴承的影响水平是一致的,因此忽略驱动电机、轴承座等微小振动对试验结果的影响。根据舰船轴系实际运转情况,试验台轴转速范围设计为40~200 r/min,转速间隔40 r/min,载荷分为0.2、0.3、0.4 MPa共3个工况。频率0~1 000 Hz内的垂向和横向振动总值如图12所示。
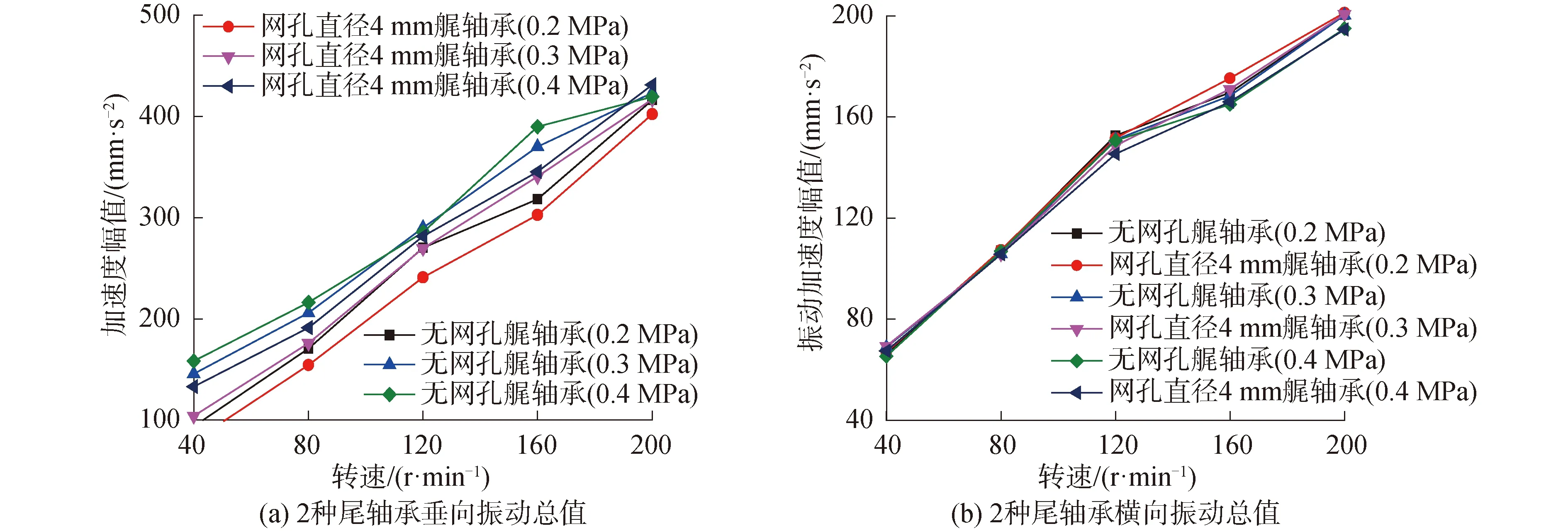
图12 2种尾轴承的垂直振动总值和横向振动总值Fig.10 Total vertical vibration and lateral vibration of two kinds of stern bearings
由2种尾轴承的振动总值图可以发现,轴系转速升高,轴承受到的径向激励能量增大,2种尾轴承的振动总值都相应升高,图12的垂直、横向振动总值都是同样的递增趋势;随着载荷的增大,由于液压油缸加载方向为垂向,垂向承载方向上的外激励能力增大,尾轴承的垂向响应幅值也就相应增大,如图12(a)所示,但网孔设计产生一定的作用,同等条件下的振动衰减能力得到了体现。另外,横向振动总值图(图12(b))显示承载方向上的载荷变动对横向振动的影响很小,有无网孔的区别不大。这些试验结果说明水润滑橡胶尾轴承底部承载区的轴向网孔设计虽然对横向振动衰减不敏感,但对承载方向的振动衰减作用较为明显,这就可以为后续更优化的板条结构设计研究提供了基础。
5 结论
1)水润滑橡胶尾轴承底部承载区的轴向网孔设计可以降低轴承固有频率,网孔直径为4 mm的尾轴承相较于其他网孔直径效果更加明显。
2)在橡胶尾轴承底部板条开设轴向网孔可以有效地降低受到外激励时的振动响应幅值。
3)橡胶尾轴承底部板条开设轴向网孔的设计对垂向振动的衰减效果明显,对横向振动的衰减不敏感。

