不完全正交的变参数H-IGMRES(m)算法

于春肖， 杨艳芳， 井丁卉

(燕山大学 理学院 河北 秦皇岛 066004)

0 引言

在科学和工程领域中,很多问题最终都可归结为大型线性方程组的求解,文献[1]提出的基于Galerkin原理的GMRES(m)算法是公认的求解大型非对称线性方程组较为成功的方法之一,同时也是快速多极边界元法中的求解器。

随着GMRES算法和相关知识被广泛学习,很多学者也对该算法进行了优化和改进。一种方法是采用预处理技术[2-4]。刘晓明等[5]将GMRES方法应用于油藏数值模拟计算问题,利用矩阵分块技术,采用块拟消去法(PE)对系数矩阵进行了预处理。于春肖等[6]提出ILU预处理Householder-GMRES(m)算法,通过降低系数矩阵的条件数达到加快收敛的目的。关朋燕等[7]将多项式预处理与加权GMRES(m)相结合,构造出一种新的方法,减少了计算量。于春肖等[8]通过改变重启动参数m的值提出VRP-HGMRES(m)算法,该算法有效地避免了因重启动参数的选取不当而造成的问题。 文献[9]将稀疏矩阵的小特征值对应的特征向量加入Krylov子空间。于春肖等[10]提出一种截断型IGMRES(m)新算法,此算法是基于FMM的Krylov子空间投影类方法。郝雪景等[11]提出基于不完全正交的变参数IGMRES(m)算法。Walker[12]对GMRES算法进行改进,提出一种基于Householder 变换的GMRES(简称H-GMRES)算法。

本文将利用截断技术[13-14]给出一种不完全正交的变参数H-IGMRES(m)算法,使计算量大大减少,并结合数值算例分析该算法的高效性。

1 H-GMRES(m)算法

在实际计算中,H-GMRES(m)算法构造Hessenberg矩阵元素和Krylov向量时都要用到较长的递推式,从而导致消耗的计算时间很长,迭代过程数值也不稳定。这种算法的具体步骤为:

1) 给定重启动参数m和误差上界ε>0,取初始值x(0)∈Rn,计算r(0)=b-Ax(0),β=‖r(0)‖2。

2) 计算P1=I-2ωωΤ,其中：‖ω‖2=1；P1r(0)=βe1；v1=P1e1。

3) 对于j=1,2,…,m，令cj=PΤAvj(当j=1时,有P=P1成立),然后计算

vj+1=Pj+1Pj…P1ej+1，hj=Pj+1cj。

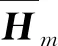
4) 如果‖r(0)-Azm‖2<ε，则x=x(m),迭代停止；否则x(0)=x(m),m=m+1且转向1)再一次迭代,直到满足给定的误差上界为止。

2 H-IGMRES(m)算法与收敛性分析

2.1 H-IGMRES(m)算法

1) 初始化:给定重启动参数m和误差上界ε>0,设置截断指标q0,取初始值x(0)∈Rn,计算

r(0)=b-Ax(0),β=‖r(0)‖2。

2) 计算P1=I-2ωωΤ,其中‖ω‖2=1；P1r(0)=βe1；v1=P1e1。

3) 对于j=1,2,…,m有不完全正交化,令cj=PΤAvj(当j=1时,有P=P1成立),然后计算

vj+1=Pej+1，hj=Pj+1cj。

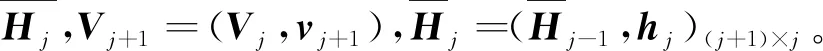
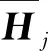
求解最小二乘问题

得出原方程组的近似解x(m)=x(0)+zm=x(0)+Vmym。

4) 如果‖r(0)-Azm‖2<ε，则x=x(m),迭代停止；否则x(0)=x(m),m=m+1且转向1)再一次迭代,直到满足给定的误差上界为止。

2.2 收敛性分析

为研究这种截断型H-IGMRES(m)算法的收敛形态,这里将H-IGMRES(m)算法和H-GMRES(m)算法结合起来,以建立H-IGMRES(m)算法的收敛性理论。

定义Vm+1=(v1,v2,…,vm+1),可以证明,如果H-IGMRES(m)算法在m步中断且Vm+1列满秩,则得到的数值解为准确解x*。另外,当q0=1时,H-IGMRES(m)算法与H-GMRES(m)算法相同。为讨论方便,选取Km=span{r(0),Ar(0),…,Am-1r(0)},将H-IGMRES(m)算法进行m步迭代后的数值解表示为x(m)(HI),残余向量表示为r(m)(HI); 将H-GMRES(m)算法进行m步迭代后的数值解表示为x(m)(H),残余向量表示为r(m)(H)。

定理1假设Vm+1列满秩，则H-IGMRES(m)算法和H-GMRES(m)算法在Km上的残值范数满足

‖r(m)(HI)‖≤S(Vm+1)‖r(m)(H)‖。

(1)

其中Vm+1由不完全正交化过程生成,S(Vm+1)=‖Vm+1‖‖Vm+1+‖,Vm+1+是Vm+1的广义逆矩阵。如果H-IGMRES(m)算法在m步中断,即hm+1,m=0,则x(m)(HI)=x*。

因此

(2)

因此,式(2)变成

‖r(m)(HI)‖=‖Vm+1(Vm+1+r(0)-Vm+1+AVmym)‖。

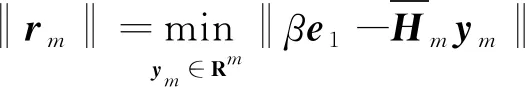
因此可得

所以式(1)成立。

3 数值算例

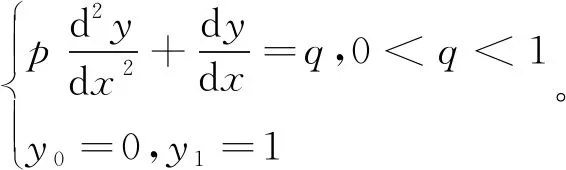
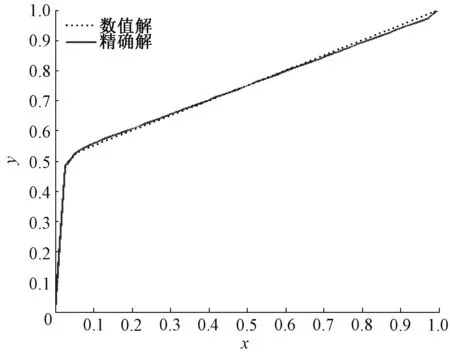
图1 精确解与数值解的比较Figure 1 Comparison of exact solution and numerical solution

Ay=b,A∈R(n-1)2×(n-1)2,y,b∈R(n-1)2。

如果选取p=0.01,q=0.5,n=40,初始向量为y(0)=(0,…,0)Τ,误差上界为t=1e-6,当m=10时,取截断指标为9,用H-IGMRES(m)算法求解该线性方程组,将得到的数值解与精确解进行比较,如图1所示。从图1可看出,数值解和精确解完全吻合,证明此算法的可行性。

下面选取n=100,分别用H-IGMRES(m)算法和H-GMRES(m)算法求解这个线性方程组。当重启动参数不同时,两种算法所需的迭代次数和得到的残值范数如图2所示,两种算法所需的运行时间见表1。从图2和表1可看出,重启动参数不同时,H-IGMRES(m)算法与H-GMRES(m)算法相比,前者迭代次数和运行时间较少,说明新算法提高了计算效率,并且具有更高的计算精度。

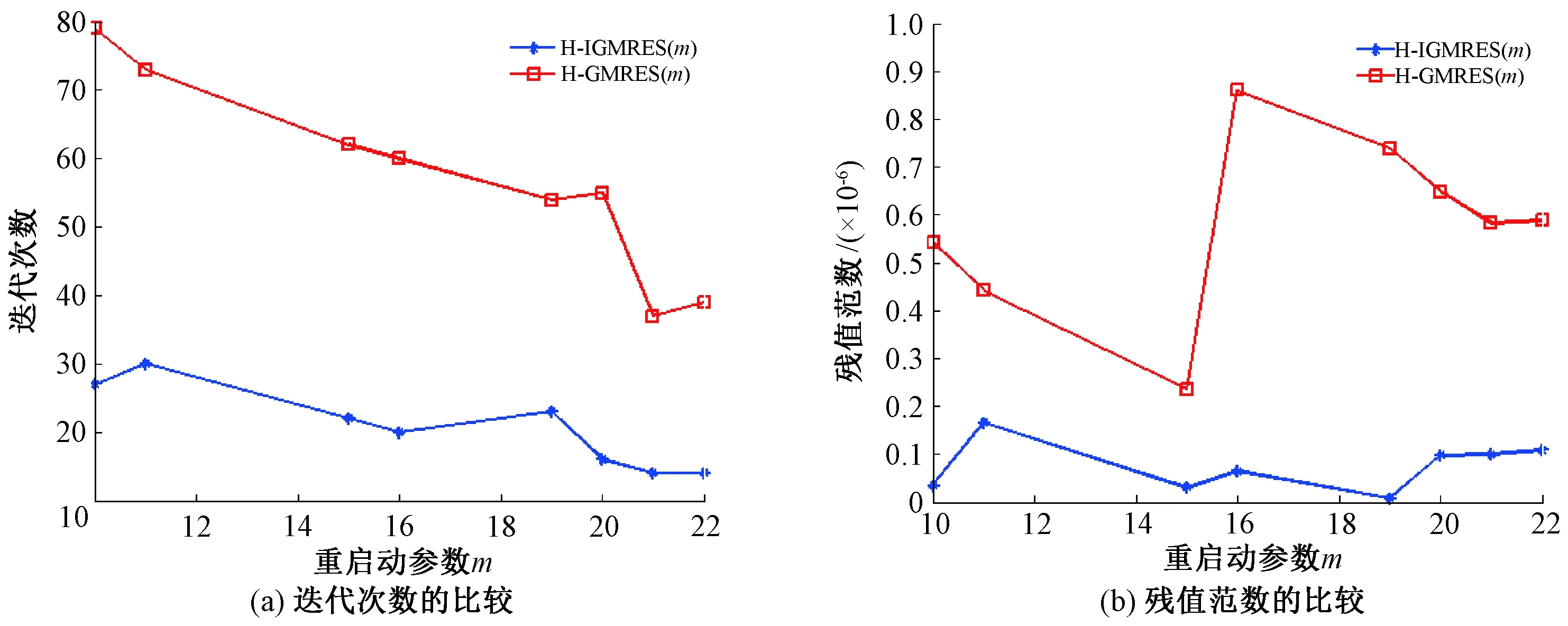
图2 两种算法计算效率与计算精度的比较Figure 2 Comparison of computational efficiency and accuracy between two algorithms

表1 当重启动参数不同时,两种算法运行时间比较(m=10)Table 1 Comparison of running time under different meshes for the two algorithms(m=10)

例2考虑如下二维Possion方程,其中Ω{(x,y)|0≤x≤1,0≤y≤1}，u(x,y)为温度分布函数。

令f(x,y)=2π2sin πxsin πy,将求解区域沿x方向和y方向进行等分,由五点差分法可得Au=b,A∈Rn2×n2,u,b∈Rn2×1。

当n=35时,选取重启动参数m=20及截断指标q0=9,分别用高斯消元法和H-IGMRES(m)算法求解线性方程组,其结果分别如图3(a)和3(b)所示。

图3 温度分布Figure 3 Temperature distribution

由图3可以看出,两种算法的计算结果完全一致,这表明H-IGMRES(m)算法是正确的。截断指标可以在1～19中取值,不同的截断指标对计算速率、计算精度、运行时间的影响如图4所示。

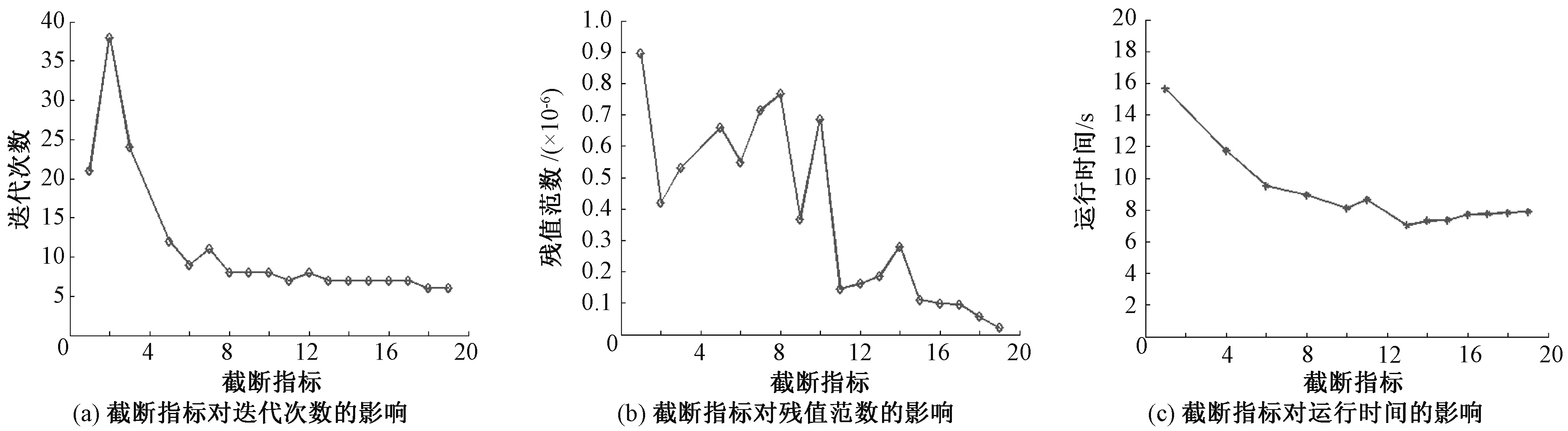
图4 截断指标对计算速率、计算精度、运行时间的影响Figure 4 Effect of truncation index on computional rate, computional accuracy, operation time

由图4可看出,迭代次数和残值范数随截断指标的增大呈下降趋势,运行时间也在突降之后逐渐趋于平稳,说明截断技术在保证计算精度的前提下提高了计算效率。当m=10时,随着计算规模n的不断增大,当残值范数满足给定的误差上界时,H-IGMRES(m)算法总的运行时间要比H-GMRES(m)算法少很多,进一步说明了H-IGMRES(m)算法的优越性,见表2。

表2 不同网格下两种算法运行时间比较(m=10)Table 2 Comparison of running time under different meshes for the two algorithms(m=10)

4 结论

1) 提出了H-IGMRES(m)算法,对算法的收敛性进行了理论分析。

2) 数值算例表明H-IGMRES(m)算法的计算结果和精确解吻合,说明该算法的有效性。

3) 分析了截断指标的选取对算法的计算精度和效率的影响,证明了H-IGMRES(m)算法的计算效率和精度都高于H-GMRES(m)算法。