基于改进蚁群算法的六自由度机械臂路径规划

赵华东， 雷超帆， 江 南

(郑州大学 机械工程学院 河南 郑州 450001)

0 引言

在工业4.0大背景下，工业机器人技术及产品已成为制造业中不可或缺的部分，同时也引发了国内外专家对相关技术的研究热潮。机械臂的路径规划问题是指在满足工作条件的基础上，寻找一条从初始点到目标点距离最短且能避开障碍的最优路径[1]。具有代表性的规划方法主要有自由空间法和人工势场法等[2]。文献[3]借助C空间法的思想，构造障碍物映射至C空间的转换关系，实现机械臂在线实时避障，但这种空间映射方法的计算量较大，尤其是对于关节数较多的机械臂而言，适用性较差。文献[4]通过构造引力场和斥力场，有效避免了碰撞的发生，很好地解决了机械臂在处理全局规划中的避障问题，但由于势场法的固有缺陷，该方法容易陷入局部最小处，规划效果欠佳。文献[5]提出了基于速度的C空间法来实现动态环境中的路径规划，但该方法仅适用于移动机器人。文献[6]利用A*算法与动力学约束相结合，达到避免碰撞实现路径规划的目的，但是这种方式需要进行大量的动力学计算，且公式推导极其复杂，不适用于多关节型机械臂。本文以ABB1410型号机械臂为研究对象，使用D-H法构建机械臂模型，进而推导出其正、逆运动学变换公式，实现末端执行器从空间坐标至关节角度的映射；通过合理的建模方式对机械臂和障碍物进行简化，设计碰撞检测方法；对蚁群算法进行了改进，以此实现机械臂在工作空间中的避障路径规划，并通过模拟机械臂的避障运动，对该方法的可行性进行了验证。

1 机械臂运动学研究

1.1 D-H运动模型的建立

D-H法是由Denavit和Hartenberg于1955年设计的一种表示机械臂各连杆间运动关系的通用方法。其基本原理是在机械臂的关节处设定坐标系来表示相连刚体杆件的空间位姿，使相邻两连杆间的空间位置关系通过4*4阶层的齐次坐标变换矩阵进行描述[7]。通过六连杆间依次变换，最终得到机械臂末端执行器相对于底座的位姿。

以ABB1410型号机械臂为例，建立的D-H运动模型如图1所示，连杆参数的数值如表1所示。

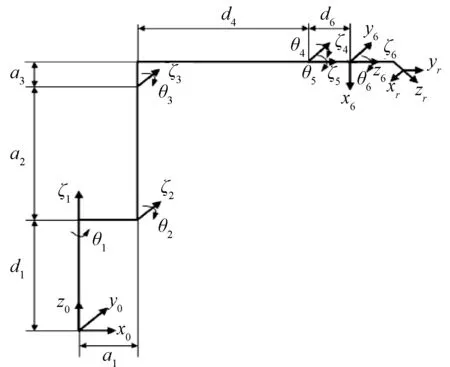
图1 ABB1410型号机械臂的D-H运动模型Figure 1 D-H motion model of ABB1410 manipulator

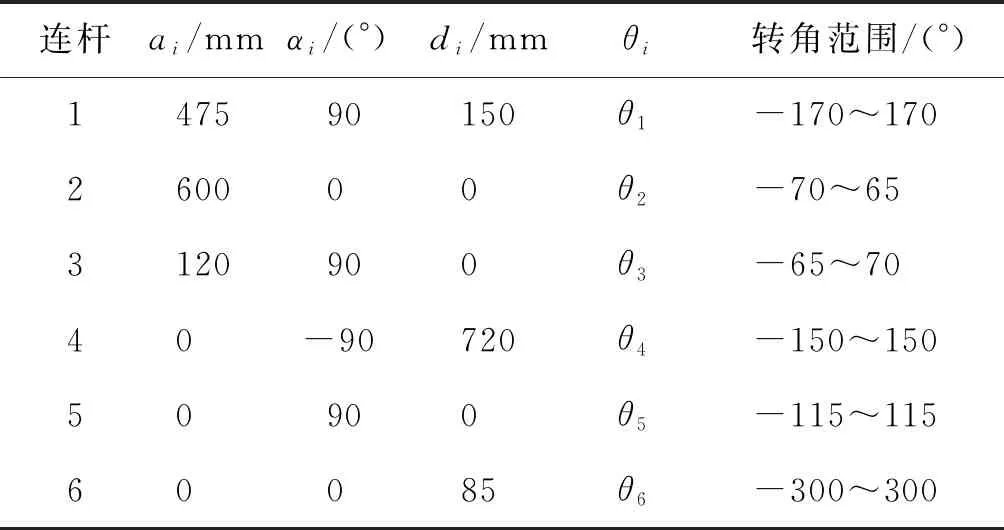
表1 连杆参数的数值Table 1 Number of connecting rod parameters

1.2 正运动学分析

机械臂的正运动学是指在已知机械臂各个连杆的尺寸大小后，给定其关节处的转角、速度、加速度等参数，计算出末端执行器处的位姿和运动状态[8]。假设某时刻机械臂六个关节的转动角度分别为θ1、θ2、θ3、θ4、θ5、θ6，已知相邻两杆间表示位姿的齐次变换矩阵为

Tn=Rot(z,θn)Trans(0,0,dn)Trans(αn,0,0)Rot(x,αn)=

根据表1中的连杆参数，可以得到ABB1410型号机械臂六个关节间的转换关系为

式中:c、s分别表示余弦函数和正弦函数；n-1Tn表示相邻两关节间的坐标转换关系。在求出六个连杆间的转换关系后，不难求得末端执行器与基坐标系之间的转换公式为

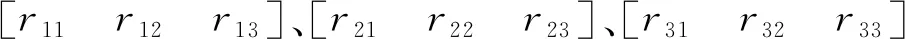
1.3 逆运动学分析

逆运动学是指在已知机械臂末端执行器坐标系的位姿矩阵后，通过对正运动学变换矩阵的反向求解，得到机械臂各个关节处的旋转角度。

采用矩阵逆乘的方法求解逆运动学解的过程为

由于推导过程烦琐，其具体过程就不在本文中展开叙述。根据Picper准则可知，机械臂逆运动学的解并不具有唯一性。因此，在实际应用中，应根据机械臂具体的避障要求以及路径规划的运动轨迹来判断机械臂所对应的逆解。

2 机械臂碰撞检测

2.1 机械臂与障碍物模型简化

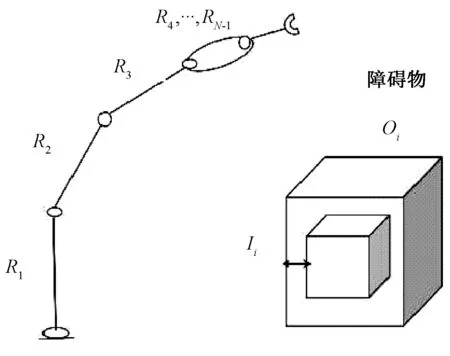
图2 机械臂简化模型Figure 2 Simplified model of the manipulator

采用长方体包络法将机械臂与障碍物抽象简化。具体做法是将机械臂连杆和工作空间中需要规避的不规则形体的障碍物用最小体积的六面体包裹起来。为了简化运算，将包络机械臂连杆的长方体看作一条直线，而将连杆长方体的边长叠加到障碍物长方体中。机械臂简化模型如图2所示。

最终，只需判断连杆直线与包络障碍物长方体的六个平面间的位置关系，即可完成碰撞检测。

2.2 碰撞检测

假设关节i和i+1处的坐标分别为p1(x1,y1,z1)和p2(x2,y2,z2)，那么连杆li所处直线的方向为H=(x2-x1,y2-y1,z2-z1)。长方体某一平面的四个顶点分别为s1(x1,y1,z1)、s2(x2,y2,z2)、s3(x3,y3,z3)、s4(x4,y4,z4)，该平面S的法向量为M(m1,m2,m3)。运用空间几何学知识可知，当M·H=0时，直线与平面平行；当M·H≠0时，说明直线与平面相交，必定存在着某个交点p0(x0,y0,z0)。交点为碰撞点需要同时满足两个条件：其一，交点必须处于连杆线段上；其二，交点要在空间平面的内部。连杆线段i若要与平面S相交，需要满足以下条件：

在完成连杆线段i与平面S的碰撞判断后，接下来用同样的方法判断连杆li与障碍物长方体的其他五个平面是否碰撞，对于机械臂另外五个连杆的判断也同样采用这种方法进行求解。

3 三维空间建模

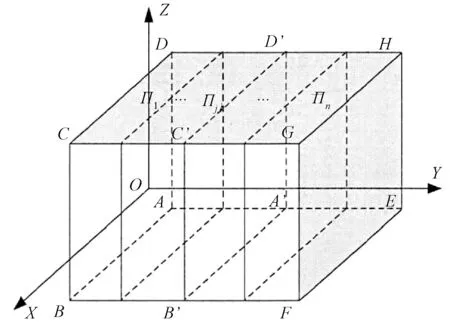
图3 三维空间规划Figure 3 Three-dimensional space planning

三维空间建模的具体方法如下：沿坐标轴方向构造包含初始点、目标点及障碍物的三维空间立方体区域ABCD-EFGH，该立方体区域即为作业空间的规划区域。在完成作业空间的规划后，采用等分法对空间进行划分，得到三维路径规划所需要的路径节点。首先沿AE边线将空间ABCD-EFGH进行等距划分，得到n个平面Πi(i=1,2,…,n)，然后再沿AB边线对这n个平面进行m等分，最后沿AD边线进行m等分，这样就将平面Πi(i=1,2,…,n)离散成m×m个栅格，三维空间规划如图3所示。

通过上述步骤，将三维规划空间离散为一系列三维空间点的集合。

4 基于改进蚁群算法的路径规划

4.1 基本蚁群算法

蚁群算法是模拟蚁群觅食行为的启发式智能算法[9-10]，该算法的实现步骤如下。

(1) 初始化算法参数。在搜索之前，需要给蚁群算法的几个重要参数赋予初始值，初始值合理与否直接影响着算法搜索的性能[11]，蚁群算法的重要参数包括蚂蚁数量、信息素启发值、适应度启发值及信息素衰减系数。

(2) 算法搜索过程。蚂蚁从当前点移动至下一路径点时，根据可视域内各个点的选择概率来决定移动目标，蚂蚁k在t时刻从i点移动至j点的概率可以表示为

式中：集合{allowed}表示蚂蚁k下一步所能选择的路径节点的集合；τij(t)表示在t时刻从i点至j点路径上的残余信息素大小；δij(t)表示在t时刻从i点至j点路径上的能见度；α表示信息素启发值；β表示适应度启发值。

(3) 局部信息素更新。每当蚂蚁完成一次路径的搜索，就要按照局部信息素更新策略对经过路径上的信息素进行更新，更新公式为τij=(1-ξ)τij，其中：τij表示以点(i,j)为信息素载体的信息素浓度；ξ表示信息素衰减系数。

(4) 全局信息素更新。当一次迭代中的蚂蚁都完成从出发点到终点的搜索后，要进行全局信息素的更新，更新公式为τij(t+1)=(1-ρ)τij(t)+Δτij(t)，其中：ρ表示信息素挥发系数。

4.2 蚁群算法的改进

4.2.1建立可视域搜索空间 为降低搜索空间的复杂程度，将机械臂末端执行器的运动简化为沿x、y、z三个轴方向上的直线运动，其中沿x轴方向的最大移动距离为Lx,max，沿y轴方向的最大移动距离为Ly,max，沿z轴方向的最大移动距离为Lz,max。这样，当蚂蚁对下一路径点进行搜索时，就会相对于当前位置形成一个可视域搜索空间。按照此种方法，将蚂蚁的搜索限制在一定区域内，简化了搜索空间，提高了蚁群算法的搜索效率。

4.2.2设置信息素浓度τij的上、下限 在蚁群算法的寻优过程中，路径上残余信息素浓度τij的大小严重影响着蚂蚁的判断，决定着收敛结果的质量。当信息素浓度过高时，蚂蚁搜索将会失去随机性，算法陷入局部最优；反之，当信息素浓度过低时，算法容易陷入早熟收敛。因此，通过对信息素浓度设置上、下限，避免算法的早熟和局部最优，增减算法的正反馈作用，公式如下：

式中：τx表示局部或全局更新计算所得到的信息素浓度大小。

4.2.3挥发系数ρ的自适应调节 挥发系数ρ反映了蚁群的全局搜索能力和算法收敛的速度。当ρ值较大时，信息素的浓度衰减较快，由正反馈机制占据主导地位，算法随机性较差；而当ρ值较小时，算法将陷入随机搜索，正反馈作用降低，进而导致收敛速度减慢。对ρ值采用自适应调节策略，公式如下：

式中：ξ∈(0,1)；N表示算法的迭代次数。

5 仿真结果与分析

5.1 算法实现流程

为了验证本文方法实现六自由度机械臂路径规划的可行性，对其进行了仿真验证。将机械臂工作空间抽象化，使用长方体包络法简化障碍物模型，通过蚁群算法在已知工作环境中寻找一条合适的规划路径，得到组成路径的节点坐标，再将该节点依次作为机械臂执行器的移动目标点，根据逆运动学计算公式求解每一目标点所对应的关节角度，可得到多组关节角度解的集合。任选一组解进行碰撞检测，若不发生碰撞，则该解满足路径规划需求，否则进行下一组解的碰撞检测。若所有的解均不满足规划需求，则将该路径节点视为障碍点，重新进行路径规划，直至所有路径节点均不发生碰撞。

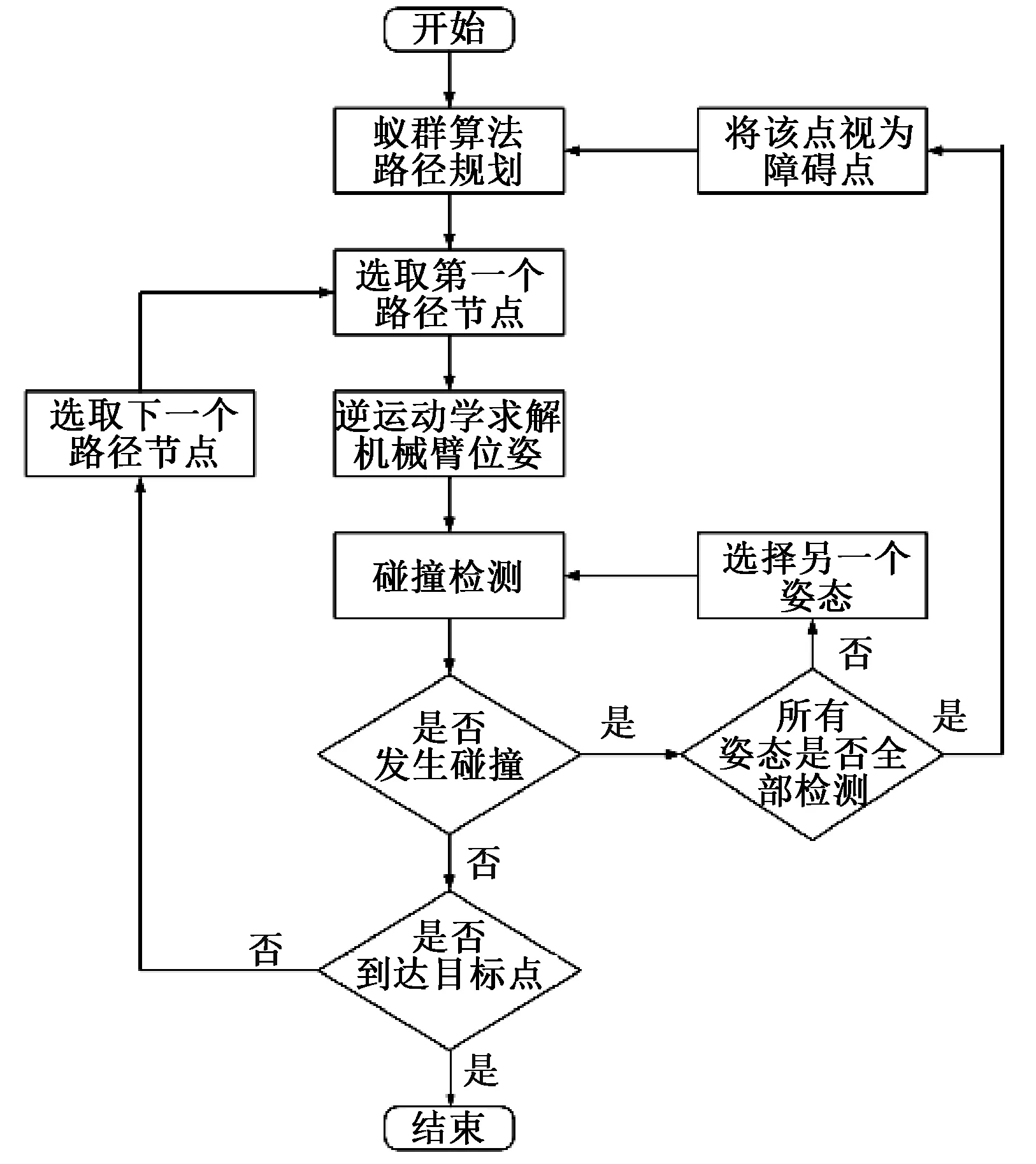
图4 算法实现流程Figure 4 Algorithm implementation flow chart

算法实现流程如图4所示。

5.2 仿真结果分析

利用仿真环境为Matlab 2014b，CPU型号为Inter i5-6500，内存为8 GB的计算机分别对优化后的蚁群算法和普通蚁群算法进行仿真对比。机械臂工作空间为2 m*2 m*1 m，离散点划分数量为20*20*10。初始点坐标为(6,5,2),目标点坐标为(13,6,10)。

根据文献[11]中的实验结果设置算法参数，蚁群数量m为50，迭代次数N为100，信息素启发值α为1，适应度启发值β为5，挥发系数ρ为0.7，仿真结果对比如图5所示。

观察仿真结果可知，在相同的参数条件下，改进蚁群算法搜索到的路径长度更短，且迭代速度更快。改进蚁群算法和普通蚁群算法的路径长度分别为1.941 m和2.119 m，迭代次数分别为38次和65次，寻优时间分别为1.636 s和2.823 s。

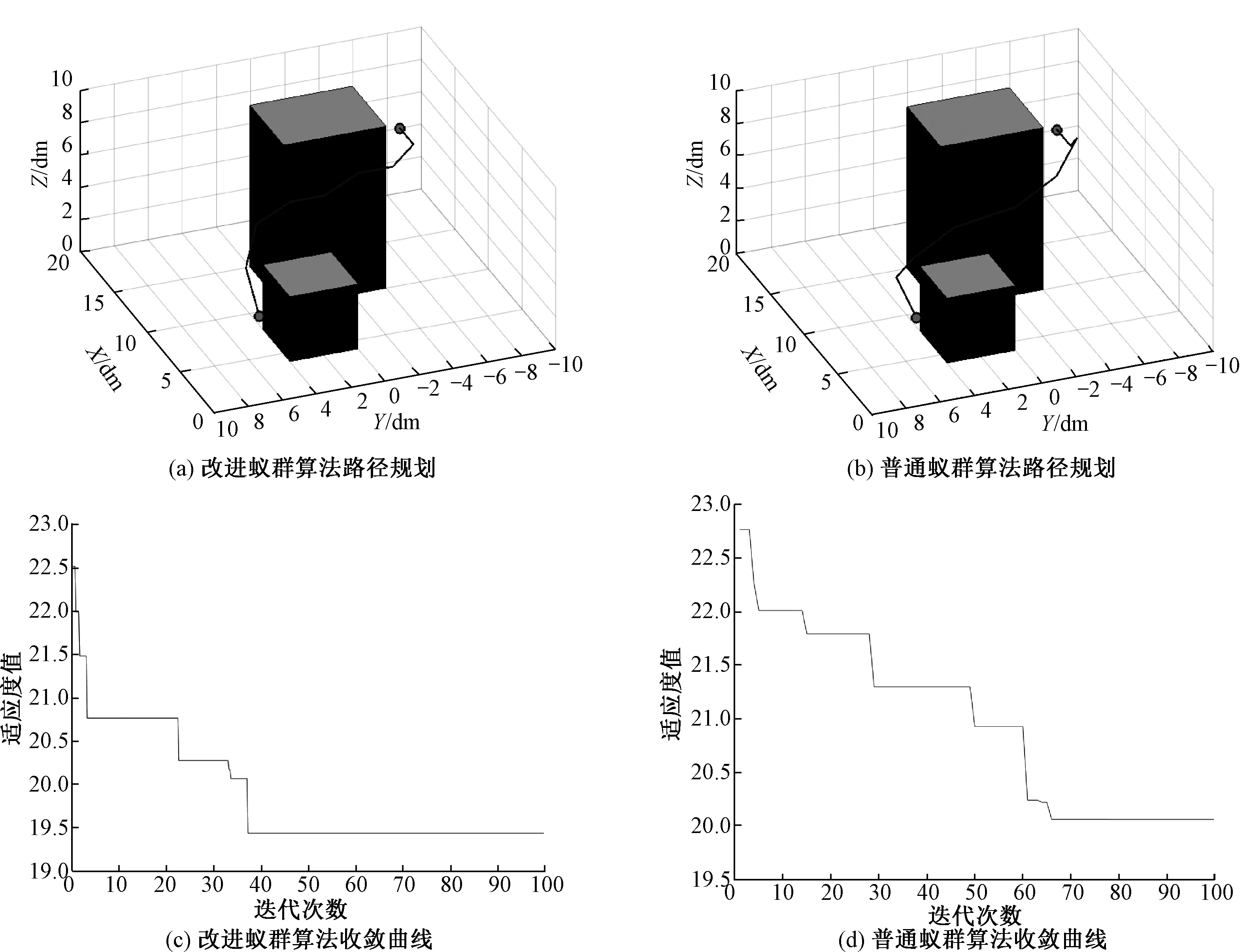
图5 仿真结果对比Figure 5 Comparison of simulation results

选择改进蚁群算法路径规划的结果作为机械臂的运动路径，机械臂在路径节点的位姿坐标和关节转角如表2所示。机械臂在沿规划路径运动的过程中，六个关节转角随时间的变化曲线如图6所示。表2和图6中关节转角的数据均为实际转角与π的比值。结果表明，每个关节角的变化都是平滑且连续的曲线，并未有突变情况发生，符合机械臂运动学规律，路径规划有效。

根据上述路径规划结果，利用RobotStudio软件模拟机械臂的避障运动过程，观察可知，机械臂机身及末端执行器均未与障碍物发生碰撞，证明碰撞检测算法有效。机械臂运动仿真过程如图7所示。结果表明，在采用本文的改进蚁群算法对空间六自由度机械臂进行避障路径规划时，能够快速、准确地搜寻到一条符合机械臂运动要求且避开碰撞的最优路径。

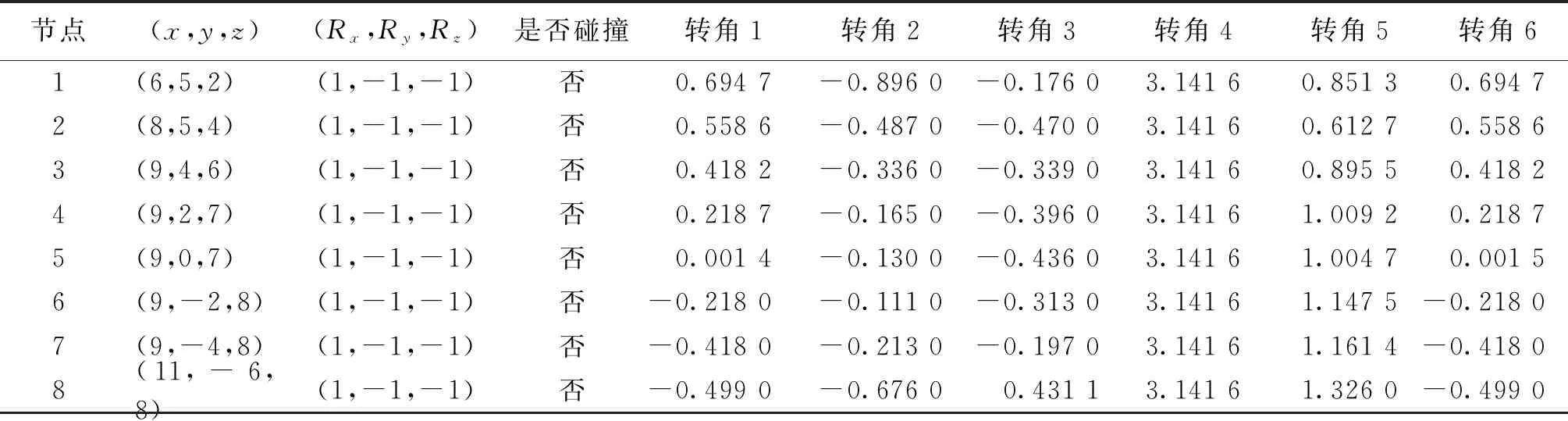
表2 路径节点的位姿坐标和关节转角Table 2 Pose coordinates and joint angles of the path nodes

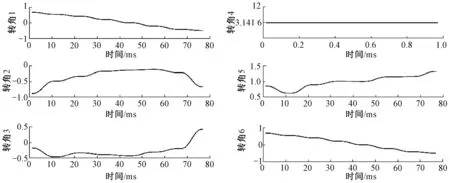
图6 关节转角随时间的变化曲线Figure 6 Joint angle curve changing with time

图7 机械臂运动仿真过程Figure 7 Simulation process of manipulater motion

6 结论

本文以ABB1410型号的六自由度空间机械臂为研究对象，首先对其进行运动学分析，建立D-H运动模型，推导正、逆运动学变换公式，得到从空间坐标到关节转角的转换关系。然后设计机械臂与障碍物碰撞检测算法，抽象化三维空间模型。 对蚁群算法进行改进，使用改进后的蚁群算法完成了机械臂在工作空间的路径规划。仿真结果验证了该方法的可行性，为空间六自由度机械臂提供了快速、精确的路径规划方法。