逻辑型决策蕴涵
张少霞, 李德玉,2, 翟岩慧,2
(1. 山西大学 计算机与信息技术学院 山西 太原 030006; 2. 山西大学 计算智能与中文信息 处理教育部重点实验室 山西 太原 030006)
0 引言
形式概念分析是一种从形式背景建立概念格来进行数据分析、知识表示和规则提取的强有力工具。蕴涵是形式概念分析中进行知识表示的基本形式,决策蕴涵[1-7]是蕴涵在决策情形下的扩展。然而,决策蕴涵并不能够表达所有的决策知识,即存在信息的损失。这是因为决策蕴涵制定了严格的决策规则,只有当条件的所有属性都被满足时,结论的所有属性才能被满足,而忽略了条件和结论的部分或全部属性不被满足的情况下所蕴含的决策知识。属性粒化是形式概念分析中粒计算方法的主要研究内容之一[8-9],可以通过逻辑算子“∧”“∨”“”将若干属性进行组合,获得逻辑公式,实现功能强大的对象描述能力。为了获取更加丰富的决策知识,本文基于逻辑公式定义了逻辑型决策蕴涵,验证了逻辑型决策蕴涵能够比经典决策蕴涵提供更丰富的决策知识;类似于经典决策蕴涵,对逻辑型决策蕴涵进行了逻辑方面的研究。鉴于利用逻辑型决策蕴涵进行知识推理时会引起矛盾的结论,而矛盾的结论不能为用户提供正确的决策,本文设计了逻辑型决策蕴涵的语义框架,该框架可以过滤掉推导结论中的矛盾。语构方面定义了闭包缩小推理规则,并证明了其相对于语义的合理性和完备性。
1 决策蕴涵
决策蕴涵有逻辑研究和数据研究两种研究方式。决策蕴涵的逻辑研究包括语义和语构两个方面:语义方面研究决策蕴涵的合理性、完备性和无冗余性;语构方面研究推理规则的合理性、完备性和无冗余性。决策蕴涵的数据研究就是决策背景中的决策蕴涵研究。
1.1 决策蕴涵逻辑
1.1.1决策蕴涵逻辑的语义
定义1[2]设C是条件属性集,D是决策属性集,其中C∩D=∅。若A⊆C且B⊆D,则称A→B是一个决策蕴涵。此时,A为该决策蕴涵的前提,B为该决策蕴涵的结论。
定义2[2]设C是条件属性集,D是决策属性集,L和L1是决策蕴涵集。定义:
1)T⊆C∪D,A→B是决策蕴涵。若AT∩C或B⊆T∩D,则称T满足A→B(或称T是A→B的模型),记为T╞A→B。若T满足L中的任意一个决策蕴涵,则T是L的模型,记为T╞L。
2) 若对于任意的T⊆C∪D,T╞L蕴含T╞A→B,则称A→B可以从L中语义导出,记为L├A→B。若任意的A1→B1∈L1都可以从L中语义导出,则称L1可以从L中语义导出,记为L├L1。
3) 若L{A→B}├/{A→B},则称L是无冗余的。
4) 若任意可以从L中语义导出的决策蕴涵都包含在L中,则称L是封闭的。
5) 对于封闭的决策蕴涵集L,若L1⊆L且L1├L,则称L1相对于L是完备的。
定义3[2]设C是条件属性集,L是决策蕴涵集,A⊆C在L上的闭包为
AL=∪{Bi|Ai→Bi∈L,Ai⊆A}。
性质1[2]设L是决策蕴涵集,A→B是一个决策蕴涵,则L├A→B当且仅当B⊆AL。
1.1.2决策蕴涵逻辑的语构 在决策蕴涵逻辑的语构方面,文献[7]提出了两条推理规则,并证明了它们相对于语义的合理性和完备性。
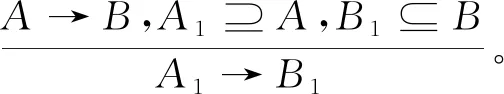
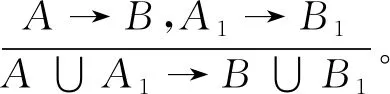
定理1[2]扩增推理规则和合并推理规则是合理的,即
1)A→B是一个决策蕴涵,若A1⊇A且B1⊆B,则A→B├A1→B1。
2)A→B和A1→B1是决策蕴涵,则{A→B,A1→B1}├A∪A1→B∪B1。
定理2[2]扩增推理规则和合并推理规则是完备的,即对任意封闭的决策蕴涵集L及其完备集L1⊆L,A→B∈L当且仅当A→B可以使用扩增推理规则和合并推理规则从L1推出。
1.2 决策背景中的决策蕴涵
定义4[5]决策背景是一个三元组K=(G,C∪D,IC∪ID),其中G是对象集,C是条件属性集,D是决策属性集,IC⊆G×C是条件关联关系,ID⊆G×D是决策关联关系。对于g∈G,m∈C∪D,(g,m)∈IC或(g,m)∈ID表示对象g具有属性m。
例1表1给出了一个与现实生活相关的决策背景K=(G,C∪D,IC∪ID),其中G={g1,g2,g3,g4},C={下雨,刮风},D={打伞,穿雨衣,打羽毛球}。表中某行与某列的交点处为1表示这个对象含有这个属性。

表1 决策背景实例Table 1 A decision context example
定义5[5]设K=(G,C∪D,IC∪ID)为决策背景,对于集合A1⊆C,A2⊆D,B⊆G,记
3)BC={m∈C|(g,m)∈IC,∀g∈B};
4)BD={m∈D|(g,m)∈ID,∀g∈B}。
定义6[5]设K=(G,C∪D,IC∪ID)为决策背景,A⊆C,B⊆D。若AC⊆BD,则称A→B是K的一个决策蕴涵。
2 逻辑型决策蕴涵的语义
2.1 逻辑型决策蕴涵的引入
尽管已经提出了完备的决策蕴涵集,但决策蕴涵仍然存在决策信息的损失,如例2所示。
例2以表1中的决策背景为例,根据定义6可以计算得到所有的决策蕴涵,即∅→∅,{刮风}→∅,{下雨,刮风}→∅,∅→{打羽毛球},{下雨}→∅和{下雨,刮风}→{穿雨衣},其中只有{下雨,刮风}→{穿雨衣}是有意义的决策知识。
事实上,表1还蕴含着其他的决策知识,如“若刮风,则不能打羽毛球”和“若下雨,则打伞或穿雨衣”等,而这些知识并不能被决策蕴涵所表达。这是因为决策蕴涵规定:只有当条件的所有属性都被满足时,结论的所有属性才能被满足,而忽略了条件和结论的部分或全部属性不被满足的情况下所蕴含的决策知识。基于此,将逻辑算子“∧”“∨”和“”引入到决策蕴涵中,进而从表1得到了更多的决策知识,如表2所示。

表2 表1中的决策知识Table 2 The decision knowledge in Table 1
决策蕴涵可以看作是只引入了“∧”算子的逻辑型决策蕴涵,因此后者可以蕴含前者的所有决策知识。以表1的决策蕴涵{下雨,刮风}→{穿雨衣}为例,表2的“下雨∧刮风→打伞∧穿雨衣∧打羽毛球”蕴含该知识。
进一步可以验证,与经典决策蕴涵相比,逻辑型决策蕴涵能够提供更丰富的决策知识。以表1中的决策蕴涵{下雨}→∅为例,显然,条件“下雨”没有蕴含任何结论。然而,当把逻辑算子“∨”和“”引入到决策蕴涵的结论中,从表1可以看出,该条件事实上蕴含了“打伞或穿雨衣,且不打羽毛球”,即表2的“下雨→打伞∨穿雨衣∧打羽毛球”。
2.2 逻辑公式
定义7[10]C是一个属性集,对于p∈C,称p为C的原子公式。用逻辑连接词“”“∧”或“∨”将C的有限个原子公式连接起来的式子叫作C的逻辑公式,简称为逻辑公式。称原子公式p及其否定p为文字。φ是C的逻辑公式,记l(φ)为φ中文字的集合。
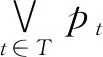
2.3 逻辑公式的模型及其偏序
定义9C是一个属性集,φ和ψ是C的逻辑公式,T⊆C。对于φ=a,若a∈T,称T满足φ。若T满足φ和ψ,称T满足φ∧ψ;若T满足φ或ψ,称T满足φ∨ψ。若T不满足φ,称T满足φ;若T满足φ,称T是φ的模型,记作T▷φ。φ的所有模型记为M(φ)。
若M(φ)=∅,称φ是矛盾的,记φ=0。若l(φ)=∅,记φ=null,且任意的T⊆C有T▷φ。
定义10C是一个属性集,φ1和φ2是C的逻辑公式,且φ1,φ2≠0。若M(φ1)⊆M(φ2),称φ2≤φ1;若M(φ1)=M(φ2),称φ2≈φ1。
性质2C是一个属性集,φ是C的逻辑公式,有下列结论成立。
1) (范式存在定理[10])φ可以通过双重否定律、德摩根律和分配率得到其析取范式和合取范式,将φ的析取范式和合取范式分别记为φ∧∨和φ∨∧。
2)φ≈φ∧∨≈φ∨∧。
3)φ=0当且仅当对于任意的φ∧∈L(φ∧∨),存在a∈C满足{a,a}⊆l(φ∧)。
4)φ1≠0,φ≤φ1当且仅当φ∧φ1=0,且当且仅当φ∧φ1=0。
证明2) 的证明过程类似于范式存在定理的证明[10],3) 显然成立。
下面证明4)。首先证明φ≤φ1当且仅当φ∧φ1=0。
充分性。因为φ1≠0,可令T⊆C且T▷φ1。又因为φ∧φ1=0,显然T▷/φ,根据定义9可知T▷φ。综上所述,任意的T▷φ1,有T▷φ,即φ≤φ1。
类似可证明φ≤φ1当且仅当φ∧φ1=0。
2.4 逻辑型决策蕴涵的语义导出
定义11C是条件属性集,D是决策属性集,φ是C的逻辑公式,ψ是D的逻辑公式。若φ≠0且ψ≠0,则称φ→ψ是逻辑型决策蕴涵。
例3给定逻辑型决策蕴涵“下雨∧刮风→打羽毛球∨跑步”和“天阴→打羽毛球”。条件“下雨∧刮风∧天阴”,同时满足这两条决策蕴涵的条件,根据决策蕴涵的合并推理规则,可以得到结论“打羽毛球∨跑步∧打羽毛球”,即“(打羽毛球∧打羽毛球)∨(跑步∧打羽毛球)”。然而,结论中“打羽毛球∧打羽毛球”是矛盾的。因此,需要定义合适的语义来解决这种矛盾。
定义12C是条件属性集,D是决策属性集,T⊆C∪D,φ→ψ是逻辑型决策蕴涵,L是逻辑型决策蕴涵集。定义:
1)T是φ→ψ的模型,若T∩C▷/φ或T∩D▷ψ,记作T╞φ→ψ。
2)T是L的模型,若任意的φ1→ψ1∈L,有T╞φ1→ψ1,记作T╞L。
定义13C是条件属性集,D是决策属性集,φ→ψ是逻辑型决策蕴涵,L和L1是逻辑型决策蕴涵集。定义:
1)φ→ψ可以从L中语义导出,记作L├φ→ψ,若满足下列条件:(a) 存在T1⊆C∪D满足T1╞L且T1▷φ;(b) 对于任意的T⊆C∪D,T╞L蕴含T╞φ→ψ。
2)L1可以从L中语义导出,若任意的φ→ψ∈L1,有L├φ→ψ,记作L├L1。
3) 若L├L1且L1├L,则称L和L1等价。
4)L是无冗余的,若任意的φ→ψ∈L,都有L{φ1→φ2}├φ1→φ2。
5)L是封闭的,若任意的L├φ→ψ,有φ→ψ∈L。进一步,若L1⊆L且L1├L,称L1相对于L是完备的。
值得注意的是,一些经典决策蕴涵中的结论并不适用于逻辑型决策蕴涵,如例4所示。
例4逻辑型决策蕴涵的语义推导不具有传递性,即L├L1且L1├L2并不意味着L├L2。
令C={下雨,刮风,天阴},D={打羽毛球},L={下雨∧刮风→打羽毛球,天阴→打羽毛球},L1={下雨∧刮风→打羽毛球},L2={下雨∧刮风∧天阴→打羽毛球}。
可以验证L├L1且L1├L2。进一步,可以验证不存在T⊆C∪D同时满足T╞L且T▷下雨∧刮风∧天阴,根据定义13可知L├/L2。例4也说明L1├φ→ψ并不意味着L├φ→ψ,其中L1⊆L。
除此之外,φ→ψ∈L并不意味着L├φ→ψ。令C={下雨},D={打伞,穿雨衣},L={下雨→打伞,下雨→打伞∧穿雨衣},可以验证不存在T⊆C∪D同时满足T╞L且T▷下雨,根据定义13可知L├/下雨→打伞。
逻辑型决策蕴涵的语义可以过滤掉推导结论中的矛盾,首先定义逻辑公式的协调式。
定义14D是决策属性集,ψ是D的逻辑公式,称
是ψ的协调式。
显然,协调式的结论中不存在矛盾。
性质3C是条件属性集,D是决策属性集,有下列结论成立。

2)φ→ψ∨ψ∨ψ1是逻辑型决策蕴涵,φ→ψ∨ψ∨ψ1和φ→null等价。
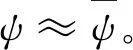
2) 显然,对于任意的T⊆C∪D,T▷ψ∨ψ∨ψ1且T▷null,即ψ∨ψ∨ψ1≈null。在此基础上,易证φ→ψ∨ψ∨ψ1和φ→null等价。
3 逻辑型决策蕴涵的语构
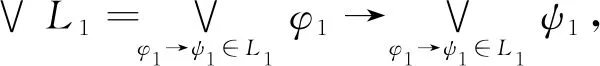
本文提出一条关于逻辑型决策蕴涵的推理规则——闭包缩小推理规则:
并证明其相对于语义的合理性和完备性。
定理3(合理性)L是逻辑型决策蕴涵集,若φ≠0,φL∨≠0且ψ≤φL∨,则L├φ→ψ。
证明首先证明L├φ→φL∨,只需证明定义13的1)中(a)和(b)成立。首先证明(a)。根据定义15可知
φL∨=∧{ψ1|φ1→ψ1∈L∨,φ1≤φ}。
(1)
因为φL∨≠0,所以存在T1⊆D满足T1▷φL∨。令
L1={φ1→ψ1∈L|φ1≤/φ,T1▷/ψ1},
(2)
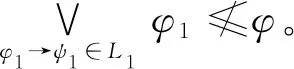
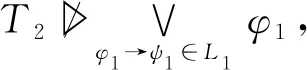
继续证明(b)。令T⊆C∪D且T╞L,为了证明(b),只需证明T╞φ→φL∨。假设T▷φ,对于任意的φ1→ψ1∈L∨,根据定义15可知必存在∅⊂L1⊆L,使得
(3)
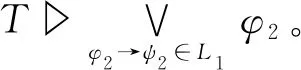
综上所述,若T▷φ,则T▷φL∨,进而T╞φ→φL∨。
最后证明L├φ→ψ,只需证明定义13的1)中(a)和(b)成立。因为L├φ→φL∨,显然(a)成立。对于任意的T⊆C∪D,T╞L蕴含T╞φ→φL∨。令T⊆C∪D且T╞L,此时T╞φ→φL∨。假设T▷φ,因为T╞φ→φL∨,由定义12可知T▷φL∨;又因为ψ≤φL∨,所以T▷ψ,进而T╞φ→ψ,(b)成立。
定理4(完备性) 闭包缩小推理规则是完备的,即对于封闭的逻辑型决策蕴涵集L,若L1⊆L且L1├L,则任意可以从L导出的逻辑型决策蕴涵φ→ψ都可以运用闭包缩小推理规则从L1导出。
证明首先证明φL∨≠0。因为L├φ→ψ,根据定义13可知,存在T╞L满足T▷φ。对于任意的φ1→ψ1∈L∨,根据定义15可知必存在∅⊂L1⊆L,使得
(4)
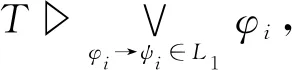
再证明ψ≤φL∨。因为φL∨≠0,可令T1⊆D且T1▷φL∨,再令
L1={φk→ψk∈L|φk≤/φ,T1▷/ψk},
(5)
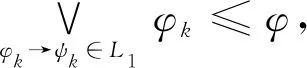
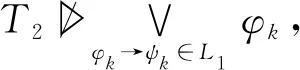
因为L├φ→ψ且T╞L,所以T╞φ→ψ。又因为T2=T∩C▷φ,所以T∩D=T1▷ψ,即T1▷ψ。综上所述,对于任意的T1⊆D,若T1▷φL∨,则T1▷ψ,即ψ≤φL∨。
已经证明φL∨≠0且ψ≤φL∨。又因为φ→ψ是逻辑型决策蕴涵,所以φ≠0。此时,根据定理3可知,运用闭包缩小规则,可以从L得到φ→ψ。
4 小结
属性逻辑是形式概念分析中重要的研究内容,决策蕴涵是蕴涵在决策情形下的扩展。与决策蕴涵相比,逻辑型决策蕴涵能够提供更丰富的决策知识。本文定义了逻辑型决策蕴涵的语义框架,该框架可以过滤掉利用逻辑型决策蕴涵进行知识推理时产生的矛盾的结论;语构方面提出了闭包缩小推理规则,并证明了其相对于语义的合理性和完备性。逻辑型决策蕴涵的数据研究,即决策背景上的逻辑型决策蕴涵,将是下一步研究的重点。

