数学计算在物流应用之案例解析一
王珂达 杨莉 吉美凤


摘 要:我们通常接触到的数学,一般都出现在教课书上-有时还晦涩难懂;接触到的物流也是现实中最普通的,没有华丽的外表;但其实两者是有相互关联的,数学隐含在物流中的每个角落,小到一张张条码,大到生产产品的规划,无一不体现数学的奥秘。利用好数学,可以让我们更加利用好物流。
关键词:数学计算、物流应用、案例解析
物流通常指物流,商量和信息流,其实信息就包含了数据,如何通过数据来挖掘信息,找到可以利用的价值,这才是数据的魅力所在,今天就让我们用几个案例,说明下物流中数据的应用。
案例(一)条形码大家都不陌生,但是其中涉及的数据大家估计还不了解,我们就举例说明其中的条码蕴含的数学知识
我们拿1个条码为例,9787121239472,其中总共位数为13位,最后一位为校验码,大家知道校验的功能就是找出差错,确保数据的准确无误,如果我说盖住其中任何1位,我可以算出盖住的数据,估计很多人不会相信,那么我们就用一个实验来证明给大家看看
首先计算出奇数位 7+9+2+2+7+7=34
然后算出偶数位之和4+3+1+1+8+9-=26
接着奇数位*3,34*3=102
将第2和第3步相加 26+102=128
取一个比结果大且以0为结尾的整数,相减,如130-128=2,大家发现,校验码正好为2,依次规律,只要知道其余的任意12个数,都可以算出其中剩余的1位数,这就是隐含在物流条码中的数学。
具体步骤如图
案例(二)生产物流线性规划
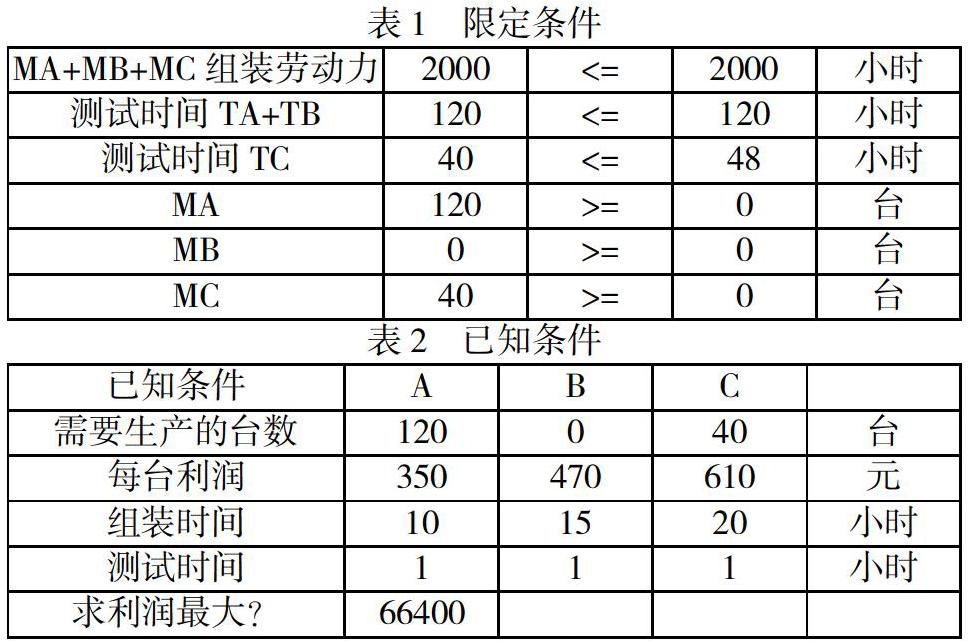
以电脑流水线为例,生产经理经常要为每周的资源分配问题而头痛,假设公司生产三种电脑,其中分为A,B和C,电脑的销售净利润分别是350元,470元和610元,其中已知净利润=销售价格-直接成本;测试设备K用于测试A型和B型电脑,可用时间为120小时,测试设备L用于测试C型电脑,可用时间为48小时,每台电脑的测试时间为1小时,可用于产品组装的劳动力为2000小时,其中A,B,C需要组装时间分别为10小时,15小时和20小时,如果我们是这位产品经理,该如何分配资源,达到每周利润最大呢?
我们用MA,MB,MC分比表示表示组装A,B和C电脑的劳动力,TA,TB和TC表示测试A,B和C电脑的时间,首先列出限定条件,如下表1所示,依据限定条件,采用EXCEL中的线性规划,求出利润最大值为66400元
案例(三)某厂生产A,B两种商品,销售单位A,B商品可获毛利分别为2与3个单位货币量,生产一个单位的A产品,需要消耗甲原料4个单位,乙原料3个单位,生产一个单元的B产品,需要销售甲原料4个单位,乙原料5个单位,由于生产原料的限制,能够提供甲乙两种原料的最大量为10和12个单位,求A,B的产量为多少时,能够获得最多的销售利润高。
根据题意,建立模型
可以求得最大利润为7.45,而商品A的数量为1.27,商品B的数量为1.63,此时达到利润最大为7.454545元。
参考文献
[1] 曾琢. 线性规划法在物流管理中的应用[J].中国市场2015.07
[2] 曹亚群.数学建模在物流管理专业教学中的应用 [J].赤峰学院学报(自然科学版)2017.05
[3] 陈宏希. 以物流管理專业为例浅谈高职院校数学建模与专业学习结合.时代教育.2011.11期
作者简介:王珂达(1976-6),男,汉族,湖南长沙人,硕士,湖南现代物流职业技术学院,研究方向:物流信息技术。

