基于改进稀疏网格替代模拟的地下水DNAPLs运移不确定性分析

高鑫宇，曾献奎，吴吉春

(南京大学地球科学与工程学院/表生地球化学教育部重点实验室，江苏 南京 210023)

近年来，随着石油化工产品和农药的广泛使用，大量有机污染物进入地下水中，造成地下水资源的污染。非水相流体(Non-Aqueous Phase Liquids, NAPLs)有机污染物是当前地下水污染研究的重要对象[1]，根据其密度相对水的密度大小，分为轻非水相流体(LNAPLs)和重非水相流体(DNAPLs)。DNAPLs难溶于水，且密度比水大，可能附着于含水层而成为地下水的长期污染源[2-3]。DNAPLs在地下水中存在水相、油相和气相，它们之间相互转化构成多相流体系统。由于DNAPLs运移过程复杂、处理费用高昂，通过数值模拟技术定量描述DNAPLs的分布和迁移转化，成为当前DNAPLs场地污染修复与风险评价的重要手段[4-6]。

由于地质环境的复杂性(如含水介质的非均质性、地层结构的分布等)、有限的观测数据以及DNAPLs的复杂运移规律，导致地下水DNAPLs运移模型的参数、结构难以进行有效识别，从而不能精确刻画其迁移转化过程，模拟结果具有不确定性。地下水模型的不确定性分析成为DNAPLs运移定量刻画的重要前提，基于贝叶斯理论的MCMC (Markov Chain Monte Carlo)模拟是当前主要的不确定性定量分析方法。Liu[7]应用MCMC对DNAPLs溶解及运移的半解析解模型进行了参数估计，并用于DNAPLs污染修复模型的污染源识别[8]。不确定性分析通常需要重复调用DNAPLs运移模型几千至几万次，模型运行时间成为当前DNAPLs运移模拟不确定性分析的重要问题。替代模型是当前克服不确定性分析计算耗时问题的有效途径，即通过建立与原始模型具有相同或接近模拟精度的模型代替原始模型。DNAPLs模拟中常见的替代模型技术有支持向量机[9-10]、克里金插值[11-12]、径向基函数人工神经网络[9]和核极限学习机[13]等。

通过MCMC进行不确定性分析时，需要不断运行模型计算似然函数，MCMC结果对似然函数高度敏感。因此，MCMC对替代模型的精度要求很高，当前研究中尚未见基于似然函数替代模拟的DNAPLs运移不确定性分析。本次研究拟采用稀疏网格(sparse grid, SG)替代模型技术，该方法适用于构建具有复杂响应关系的替代模型。SG替代模型构建过程中，为提高构建效率、减少参数空间网格冗余，一般有两种自适应方式，局部自适应(local adaptive, LA)和维数自适应(dimension adaptive, DA)。如Zhang等[14]通过一种高阶LA-SG技术建立了铀素反应性溶质运移替代模型，并通过MCMC识别得到模型参数后验分布。Zeng等[15]基于DA-SG技术建立了溶质运移替代模型，并通过MCMC进行了地下水污染源识别。替代模型的构建成本(即需运行一定数量的原始模型)与替代对象的复杂度密切相关，且随着模型参数维数的增加而显著增加。Zeng[15]等利用DA-SG建立5维溶质运移替代模型需运行原模型1 545次。Zhang等[14]通过高阶LA-SG建立6维反应性溶质运移替代模型的成本是运行原模型3 765次。Zeng等[16]使用LA-SG及约1万次原模型运行建立了10维非均质地下水流替代模型。因此，高效率、高精度的替代模型技术对于复杂、高维DNAPLs运移模拟的不确定性分析具有重要的理论和实际意义。

本次研究拟基于SG技术，将替代模型参数空间的两种网格自适应生成方式(LA、DA)相结合，进一步提高替代模型的构建效率和替代精度。此外，通过两个解析案例(5维rastrign函数、20维banana函数)和一个DNAPLs运移室内模拟模型，验证所提出的维数、局部自适应稀疏网格替代模型(DA-LA-SG)的效率和精度。

1 研究方法

1.1 稀疏网格替代模型

1.1.1基本原理

稀疏网格(SG)是一种基于Smolyak[17]规则的叠层拉格朗日插值方法，具有方法原理简单、插值精度高等优点，在水资源与水环境模拟中应用广泛。对于一维非线性函数f(x)，其叠层拉格朗日插值项U定义为：

(1)

m0=1,m1=2,

mi=2i-1ifi≥2

(2)

SG插值点的生成规则有Clenshaw-Curits规则、Gauss-Patterson规则、Uniform规则等[18]，本研究中使用Uniform规则，在[0,1]间的坐标表达式为：

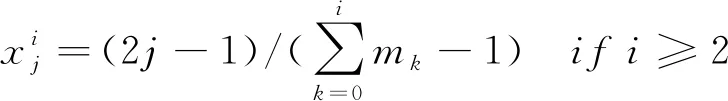
(3)

(4)

式中：L——最大插值级数；

mi——对应级数i的稀疏网格插值点的数量；

φ(x)——插值基函数，本次研究使用三次多项式基函数[18]；

c——插值系数，也叫基函数的叠层盈余，表示插值公式与目标函数在x处的差值。

当函数f(x)相对平滑时，随着插值级数i增加，叠层盈余将接近于零，所以c可以作为局部自适应的误差标准。

基于一维叠层插值方法，多维稀疏网格插值为：

i=(i1，…，iD)

(5)

式中：D——模型参数x=(x1,…,xD) 的维度；

i——ΔVi,D[f(x)]的多维插值级数向量；

ik(k=1,…,D)——第k维插值级数。

ΔVi,D[f(x)]定义为：

ΔVi,D[f(x)]=ΔUi1⊗…⊗ΔUiD[f(x)]=

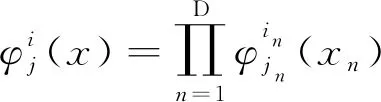
(6)

式中：j——向量(jl=1,…,mil,l=1,…,D)；

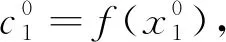
1.1.2自适应稀疏网格(Adaptive SG)

普通SG方法的插值级数向量的集合为：β={i∈Nd:λ(i)≤L}。相对于全张量网格节点，缓解了“维数诅咒”效应，但对于高维参数空间，替代模型的成本仍不可忽视。根据目标函数参数和输出之间的响应关系，通过网格自适应的生成方式，减少模型参数空间的冗余网格节点，可以进一步降低SG替代模型的成本。

(1)维数自适应稀疏网格(DA-SG)

DA-SG的基本思路[19]可以总结为：① 从级数向量(0, 0, …, 0)开始，在当前级数向量i的前邻域{i+ej: 1 ≤j≤D}(ej表示第j维为1、其他为0的单位向量)中搜索候选级数向量A，候选级数向量条件为i-ej∈Ofor1≤j≤D,ij>1，O为已有级数向量集合；②在A中找到使测试点的误差项趋于最大的级数向量k，并将其加入已有级数向量集合O中；③将k作为当前已有级数向量，重复步骤①和②，直到误差低于预定义的误差标准。这种方法结合了贪婪算法的思想，可在构建稀疏网格的同时确定对目标函数变化有最大影响的级数向量，提高了构建替代模型的效率。

图1所示为DA-SG插值节点的自适应生成过程。图1(a)～(c)所示为当前插值级数向量，图1(d)～(f)表示相应级数向量对应的网格点分布图。图1(a)中候选级数向量A包含(4，0)、(1，1)和(0，3)。首先，将A中误差项最大的级数向量i即(1，1)加入已有级数向量集合O中。然后，对该级数向量i的所有前邻域级数向量(即(2，1)、(1，2))进行候选条件测试，结果发现均满足条件，将其加入集合A中，此时A包含4个级数向量。最后，重复上述过程，寻找误差最大项，一直循环计算直至误差达到标准。

图1 二维维数自适应稀疏网格(DA-SG)示意图Fig.1 Diagrammatic sketch of two dimensional DA-SG

(2)局部自适应稀疏网格(LA-SG)

图2 二维局部自适应稀疏网格(LA-SG)示意图[18]Fig.2 Diagrammatic sketch of two dimensional LA-SG

(3)维数-局部自适应稀疏网格(DA-LA-SG)

DA-SG方法通过识别对目标函数变化有显著影响的级数向量，提高了SG构建效率，但当目标函数变化区域集中在参数空间较小区域时，DA-SG方法的效率较低。与DA-SG相比，LA-SG方法通过在非线性程度低的区域减少插值节点，克服了DA-SG的不足，但LA-SG在所有级数向量空间均构造插值节点。因此，提出将DA、LA结合的改进稀疏网格替代模型方法DA-LA-SG，能够进一步提到SG替代模型的构建效率。如图3所示，首先对目标函数进行维数自适应，寻找误差最大项；其次，在计算插值系数时进行局部自适应，判断局部自适应的标准，舍弃已满足误差标准节点的下级节点；最后，重复进行上述过程，直至维数自适应误差达到预设的标准，结束替代模型运行。

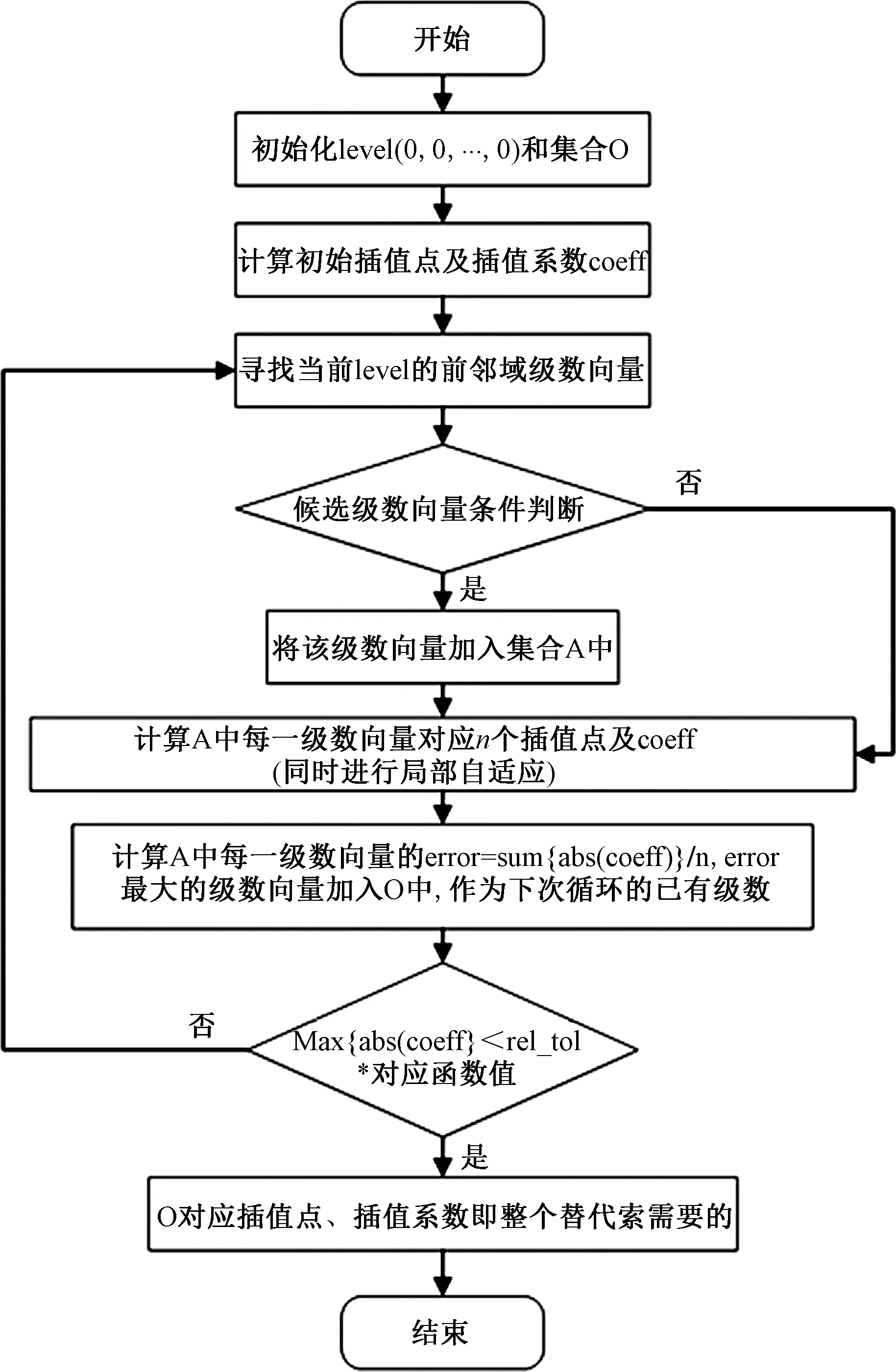
图3 DA-LA-SG算法流程图Fig.3 Algorithm flow chart of DA-LA-SG

1.2 贝叶斯不确定性分析

贝叶斯不确定性分析方法的基础是贝叶斯公式，可表示[22]为：

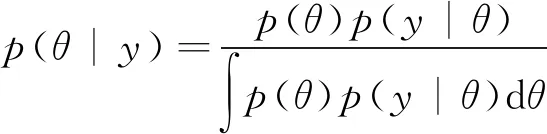
(7)

式中：p(θ|y)——参数θ的后验概率分布；

p(θ)——θ的先验概率分布；

p(y|θ)——θ的似然函数；

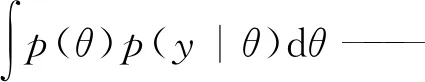
常用的似然函数为高斯函数，其自然对数表达式为：

(8)

式中：Σ——观测误差的协方差矩阵；

|Σ|——行列式。

由于p(θ|y)难以直接计算，一般采用统计抽样的方式间接获取，如MCMC模拟。MCMC方法利用构建马尔科夫链来反演模型参数θ的后验分布，通过在θ的概率空间内持续搜索，逐渐收敛于一个稳定的后验分布π(θ)。本次研究中采用最新的抽样算法DREAMzs[23]进行参数不确定性研究，基本步骤如下：①基于先验信息，设置模型参数的先验分布和马尔科夫链的起点[θi,i=1,…,N]，N表示平行马尔科夫链的数量；②将式(8)作为似然函数，利用观测数据y，通过DREAMzs抽样得到参数后验样本；③对采样得到的结果(模型参数和输出的后验分布)进行统计分析，定量分析不确定性大小。

1.3 替代模型的精度评估

采用目标函数和替代模型间的相关系数R2和相对均方根误差NRMSE[24]作为替代模型精度的评价指标。

(1)相关系数(R2)

(9)

式中：n——样本个数；

yi——目标函数的输出值；

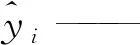
R2越接近于1，替代模型效果越好。

(2)相对均方根误差(NRMSE)

(10)

式中：|f|max——目标函数输出最大绝对值。

2 算例分析

2.1 解析案例

2.1.15维rastrign函数

选择5维rastrign函数作为本次替代模型的目标函数，用于测试DA-SG、LA-SG和DA-LA-SG等3个替代模型的效率和精度。Rastrign函数的解析表达式为：

其中，A=10,-5.12 ≤xi≤ 5.12,n=5。

图4 (a)Rastrign函数在2维参数空间上的响应面; (b)各替代模型NRMSE随样本数量的变化Fig.4 (a)Response surface of the Rastrign function in 2-D space; (b)The NRMSE of surrogates vary with the number of samples

图4(a)为目标函数在二维空间的响应面示意图。图4(b)显示DA-SG、LA-SG和DA-LA-SG等3个替代模型随着插值节点数量的增多，替代误差(NRMSE)均逐渐降低。从图中可以看出，在替代模型建立的初期(插值节点少于100)，LA-SG的替代效率(达到一定替代精度所需的构建成本)高于DA-SG和DA-LA-SG，但是插值节点数量的增多，DA-SG、DA-LA-SG的替代效率逐渐高于LA-SG。这是由于在替代模型的构建初期，插值节点分布较少，LA-SG能够更有效识别目标函数的局部特征，而随着插值节点数量增多，DA-SG方法能够有效识别对目标函数变化有显著影响的级数向量，进行插值空间的降维处理。当插值节点数量低于2 600时，DA-SG与DA-LA-SG替代模型表现基本相同，这是由于替代模型前期插值系数(误差)较大，达不到局部自适应误差标准。当插值节点数量超过2 600，DA-LA-SG表现优于DA-SG，DA-LA-SG中的部分插值节点因局部自适应而被舍弃。因此，在替代成本相同的条件下，DA-LA-SG的精度高于DA-SG。

2.1.220维banana函数

为了进一步测试高维情况下DA-SG、LA-SG和DA-LA-SG等3个替代模型的效率和精度，选择20维banana函数作为本次替代模型的目标函数，banana函数的解析表达式为：

-10≤xi≤10,1≤i≤n

图5(a)为目标函数在二维参数空间的响应面示意图。图5(b)所示为DA-SG、LA-SG和DA-LA-SG等3个替代模型随着插值节点数量的增多，替代误差(NRMSE)逐渐降低的过程。从图中可以看出，在替代模型的建立初期(插值节点少于1 000)，LA-SG的替代效率比DA-SG和DA-LA-SG高，但随着插值节点数量的增多，DA-SG、DA-LA-SG的替代效率逐渐比LA-SG高。这是由于在替代模型的构建初期，插值节点较少，LA-SG通过识别目标函数的局部特征进行插值节点的自适应，而随着插值节点的增多，DA-SG通过识别重要的级数向量进行降维处理，其替代效率逐渐升高。插值节点数量低于2 000时，DA-SG与DA-LA-SG表现基本相同，这是由于替代模型前期的插值误差较大，局部自适应过程很少发生。当插值节点数量超过2 000，DA-LA-SG表现优于DA-SG，这是由于局部自适应DA-LA-SG舍弃了部分冗余插值节点，从而提高了替代效率。

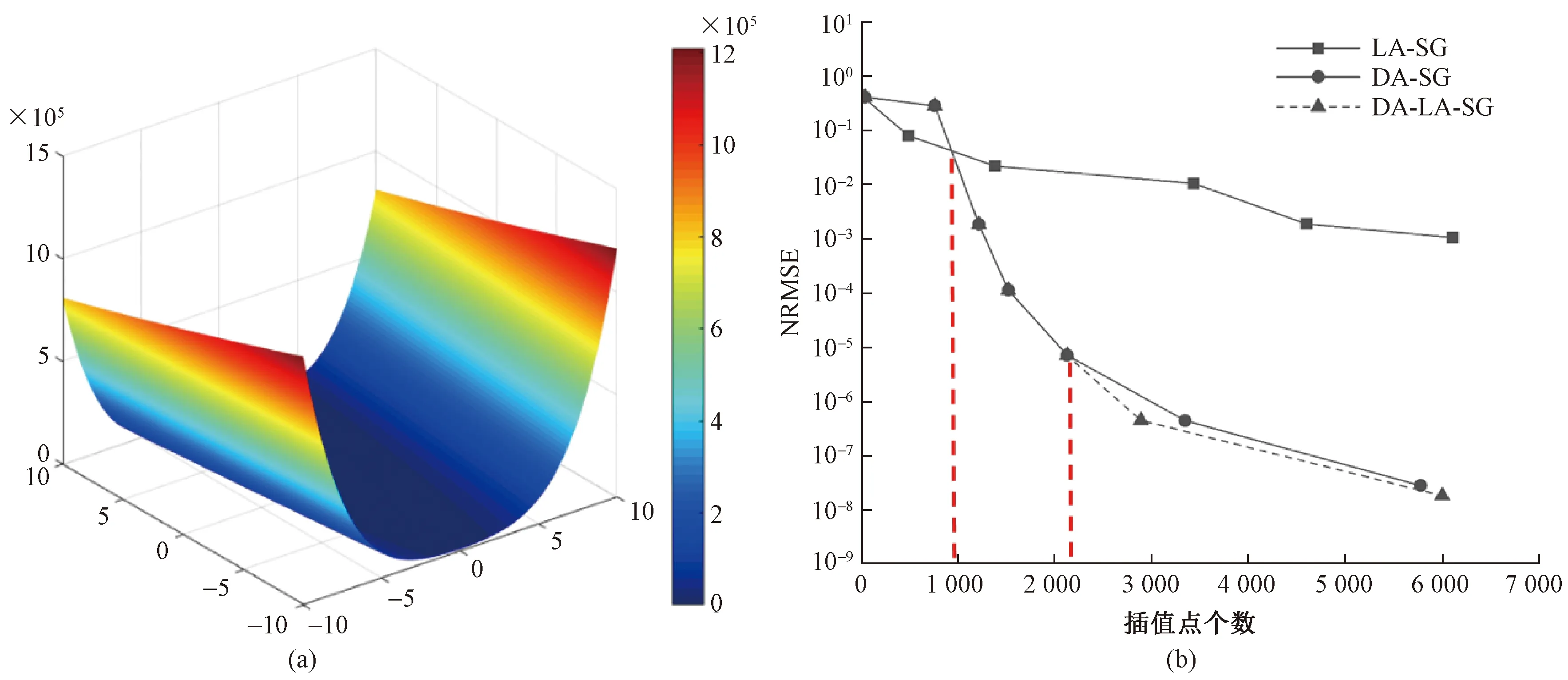
图5 (a) Banana函数在2维空间上的响应面；(b)各替代模型NRMSE随样本数量的变化Fig.5 (a) Response surface of the banana function in 2-D space; (b) The NRMSE of surrogates vary with the number of samples

2.2 二维砂箱DNAPLs运移室内实验

本次实验选用四氯乙烯(PCE)作为典型DNAPLs污染物，通过向砂箱中注入PCE的方式模拟污染物的泄露。图6(a)为二维砂箱多孔介质中PCE的运移模拟室内实验示意图。砂箱的长、宽、厚分别为0.6 m×0.45 m×0.016 m。砂箱左侧为入流边界，流速保持7.2×10-3m3/d，由蠕动泵控制。砂箱背景介质为均质多孔介质，内部分布5个低渗透介质作为透镜体模拟介质非均质性对PCE运移的影响。砂箱实验中，PCE注入点位于x=0.3 m，y=0.4 m，z=0.008 m处。通过光透法[25](LTM)实时监测砂箱中的PCE饱和度，且用作本次实验的观测数据。此外，本次案例研究采用T2VOC程序[26]对污染源注入过程的PCE运移进行数值模拟，PCE注入时间共持续80 min。图6(b)显示PCE停止注入时刻(即t=80 min)，砂箱中PCE的饱和度分布。

图6 (a)二维砂箱PCE运移实验示意图；(b)停止注入时刻PCE饱和度分布图Fig.6 (a)Diagrammatic sketch of the 2-D sandbox PCE experiment; (b)Saturation distribution of PCE after stopping injection

在实际情况下，由于有限的观测信息，一些水文地质参数难以准确给定，例如渗透率、孔隙度等。对于PCE运移模拟模型，PCE的浓度分布对含水层的渗透性十分敏感[27]。因此，本次研究中选择两个区域(背景介质和低渗透体)的渗透率(k1,k2)和孔隙度(μ1,μ2) 作为未知参数，同时将T2VOC程序中相对渗透率函数中的拟合系数(n1,n2)作为未知参数。通过观测数据(PCE的饱和度分布)，对本次PCE运移模拟的6个未知参数进行识别。

将本次砂箱实验处理为二维PCE运移问题，模拟区域在x,y,z方向上离散为35×38×1个网格单元。PCE运移数值模型中，采用Parker本构模型。此外，对PCE运移模型进行参数不确定性分析时，未知模型参数的先验分布均假定为均匀分布，范围见表1。

表1 PCE运移模型中未知参数的取值范围

2.2.1建立似然函数的替代模型

本次案例分析中，分别采用LA-SG、DA-SG和DA-LA-SG等3种方法建立lgp(y|θ)的替代模型，并对这三种替代方法的效率和精度进行对比分析。其中，替代效率表示建立替代模型的成本，替代精度为替代模型与原始T2VOC结果的接近程度。

图7 PCE运移模拟对数似然函数替代模型的NRMSEFig.7 NRMSE of surrogates for the logarithmic likelihood function

图7为砂箱PCE运移模拟对数似然函数的替代模型(DA-SG、LA-SG和DA-LA-SG)随着插值节点数量的增多，替代精度逐渐升高的过程。从图中可以看出，在替代模型的构建初期(插值节点数量小于等于100)，3个替代模型具有相接近的替代效率，替代模型的NRMSE随插值点数量的衰减速度相似。随着样本数量的增多，替代模型的替代精度均逐渐升高，但NRMSE的衰减速度与替代模型初期相比，均有所降低。DA-LA-SG具有最高的替代效率，即在相同的替代成本条件下，DA-LA-SG具有最高的替代精度，其次为DA-SG和LA-SG。在替代模型的构建初期，各参数维度上的插值节点数量较少，进行维数自适应时，所舍弃的插值节点并不明显。随着插值水平(Level)的增加，各参数维度所需的插值节点数量迅速增加，进行维数自适应能够显著减少插值节点的数量，提高替代模型的效率。

图8显示了本次PCE运移模型的对数似然函数lgp(y|θ)的响应面及其替代模型的效果。图8(a)～(c)分别表示lgp(y|θ)在不同2维参数空间上的响应面，(d)表示采用DA-LA-SG方法建立的lgp(y|θ)替代模型的效果。结果显示，建立该替代模型共需要运行原始PCE运移模型745次，原始模型与替代模型间的相关系数R2为0.999 7，替代模型的RMSE为3.63，表明通过DA-LA-SG方法建立的lgp(y|θ)替代模型具有较高的替代效率和精度。本次室内砂箱实验PCE运移模拟参数不确定性分析中，采用DA-LA-SG建立的似然函数替代模型，而无需调用原始的PCE运移模型。

图8 (a)～(c)对数似然函数在二维参数空间上的响应面；(d) DA-LA-SG替代模型效果图Fig.8 (a)～(c) Response surfaces of the 2-D logarithmic likelihood function; (d) Performance of DA-LA-SG

2.2.2基于DA-LA-SG替代模型的PCE运移模拟参数不确定性分析

图9 PCE运移模型参数的后验概率分布Fig.9 Posterior probability density of the PCE migration parameters

采用基于DREAMzs算法的MCMC模拟识别6个未知模型参数的后验分布，参数先验分布见表1。为了保证搜索效率，使用3条平行马尔科夫链，每条链长度为30 000，预热期长度为10 000，剩下的样本用于生成参数的后验分布。在MCMC运行过程中，调用基于DA-LA-SG建立的似然函数替代模型不需运行原始模型。图9为识别得到的6个模型参数的后验概率分布，坐标横轴区间表示相应参数的先验分布范围。经过MCMC参数识别，k1、k2和n1的后验概率密度呈正态分布，相对于先验分布，参数的后验分布范围明显缩小，说明这3个参数对观测数据(PCE的饱和度)比较敏感。相比之下，模型参数μ1、μ2和n2后验概率分布大致呈均匀分布，且与先验分布范围相同，因此这3个参数对观测数据不够敏感，参数识别效果较差。本次DNAPL运移模拟不确定性分析结果表明，砂箱实验中DNAPL的运移主要受介质的渗透性影响[28-29]，DNAPL在运移过程中受到弱透镜体的阻碍，由于无法克服毛细压力而在其上方聚积并侧向运移，孔隙度对DNAPL运移的影响较小。因此，对于实际DNAPL污染场地的评估与修复，场地含水层的渗透性质特别是弱透水介质分布的精确刻画，是建立准确、可靠DNAPLS运移模拟模型的重要条件。

3 结论

为克服DNAPLs运移模拟不确定性分析中的计算耗时问题，本次研究在传统稀疏网格(SG)替代模型的基础上，提出了一种将局部自适应(LA)和维数自适应(DA)两种网格生成方式耦合的改进替代模型DA-LA-SG。通过两个解析案例和一个DNAPL运移室内实验，对比分析了DA-SG、LA-SG和DA-LA-SG三种替代模型技术的表现，并将DA-LA-SG替代模型用于DNAPL运移数值模拟不确定性分析中，得到以下结论：

(1)在替代模型的构建初期，LA-SG的替代效率(一定替代精度条件下的替代成本)优于或接近于DA-SG和DA-LA-SG，随着插值节点数量的增多，DA-SG和DA-LA-SG的替代效率逐渐优于LA-SG，且DA-LA-SG具有最高的替代效率。

(2)使用改进的维数、局部自适应稀疏网格技术(DA-LA-SG)能够高效、高精度的建立PCE运移模型的似然函数替代模型。构建替代模型需运行原始模型745次，原始模型与替代模型间的相关系数R2达到0.999 7。

(3)将建立的似然函数替代模型用于PCE运移模拟参数不确定性分析，克服了因重复调用PCE运移模型导致的计算耗时问题，通过MCMC模拟获得了模型参数的后验分布。结果发现，背景介质渗透率k1、拟合系数n1和透镜体渗透率k2的可识别性较强，背景介质孔隙度μ1、透镜体孔隙度μ2和拟合系数n2的识别效果较差，这些参数对饱和度观测数据不敏感。