地下水典型非水相液体污染运移模拟的尺度提升研究

陈梦佳，吴剑锋，孙晓敏，林 锦，吴吉春

(1.南京大学地球科学与工程学院水科学系/表生地球化学教育部重点实验室，江苏 南京 210023；2.南京水利科学研究院，江苏 南京 210029)

非水相液体(non-aqueous phase liquids, NAPLs)在工业生产中应用广泛，主要包括煤焦油、氯化溶剂等，是目前地下水污染的主要污染源之一。由于NAPLs在水中的溶解度相对较低，一旦发生泄漏，就会形成一个独立自由相[1]。在饱和带中，NAPLs常以不连续的形式分布在污染源区，缓慢地溶解于地下水并随之流动扩散，逐渐形成大面积的污染羽[2-4]。

NAPLs运移模型可为制定污染修复方案提供关键技术支撑。目前，UTCHEM是一款广泛用于地下水NAPLs运移的多相流数值模拟软件。在复杂的地下水污染运移数值模拟过程中，场地面积、网格大小、运移持续时间等都对计算时间和模拟精度有显著影响[5]。一般说来，为了尽可能节省计算成本，在地下水数值模拟中尤其涉及到蒙特卡洛随机模拟时，模型的参数网格尺度一般大于实际测量的参数尺度[6-8]。为此，需要在保证模拟精度的情况下，将小尺度的参数转换为大尺度的等效参数，亦即需要尺度提升。

随着社会的发展，提出的问题变得越来越复杂，范围更大、时间段更长、水文地质条件更为复杂。对于这些问题的计算，传统的地下水数值模拟需要巨大的计算成本来保证解的精度。研究表明，对参数进行尺度提升能够非常有效地减少计算时间[9-11]。由于渗透系数的确定在地下污染物的运移模拟中起着至关重要的作用，所以尺度提升的重点是将小尺度的渗透系数进行转换，以得到数值模型尺度上的等效参数，使得大尺度模型保持小尺度上的污染羽特征[12-13]。常用的尺度提升法有简单平均法(simple averaging)、流管法(stream-tube)、简单拉普拉斯法(simple Laplacian)等[14-16]。拉普拉斯-外壳法(Laplacian with skin)是对简单拉普拉斯法的改进，是一种基于求解流动方程的渗透系数尺度提升方法，而非依靠经验，因此能够运用于各类场地。本文利用拉普拉斯-外壳法对渗透系数场进行尺度提升并建立大尺度地下水典型NAPLs数值模型，与尺度提升前的小尺度模型及基于算术平均的尺度提升模拟结果进行对比，评价拉普拉斯-外壳法的提升效果。

1 研究方法

与传统的基于算术平均的尺度提升方法相比，简单拉普拉斯尺度提升法基于求解流动方程，因此在理论与实际领域都有广泛的应用[17-20]。但是，简单拉普拉斯尺度提升方法假设所得的等效渗透系数为对角张量，一旦当小尺度的渗透系数产生的总流量不平行于参考轴，则通过这种尺度提升方法得到的模拟结果无法准确描述小尺度模型中的运移行为[21-22]。因此，针对这一缺陷，Gómez-Hernández[23]假设等效渗透系数为全张量，提出了拉普拉斯-外壳法；李良平等[24]将拉普拉斯-外壳法应用到综合实例中，论证了拉普拉斯-外壳法相较于其他尺度提升方法的优势。

渗透系数尺度提升的目的是将小尺度的渗透系数转换为大尺度的等效渗透系数，使其能运用于数值模型中，因此转换需要满2个条件：

(1)大尺度网格(block)中的水头应等于小尺度网格(cell)中水头的平均：

(1)

式中：V——大尺度网格范围；

nV——大尺度网格内小尺度网格的数目；

hV(I,J)——大尺度网格内水头/m；

h(i,j)——小尺度网格内水头/m。

(2)大尺度网格中的流量应等于小尺度网格中流量的平均：

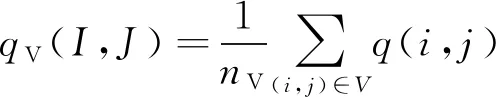
(2)

式中：qV(I,J)——大尺度网格内流量/(m3·s-1)；

q(i,j)——小尺度网格内流量/(m3·s-1)。

拉普拉斯-外壳法的一个重要特点是使用外壳区域估计实际的大尺度网格的边界条件，而不是拉普拉斯法中简单的人为定义边界条件，因此小尺度渗透系数场的区域大小要比实际含水层模型稍大，以便使模型边界附近的网格也含有外壳。大尺度模型中外壳选取、网格内水头与流量定义见图1。

对于小尺度网格的多套边界条件，计算小尺度网格中的流动：

(3)

将等效渗透系数定义为：

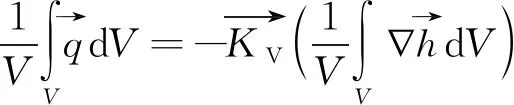
(4)

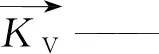
运用计算得到大尺度网格中的参数，建立超定系统方程：

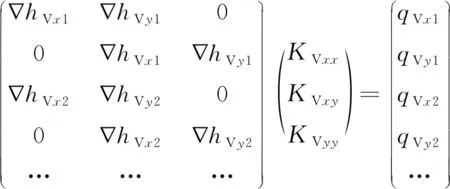
(5)

式中：Kxx，Kxy，Kyy——未知的等效渗透系数全张量的成分。

图1 尺度提升示意图Fig.1 Schematic diagram showing the scale-up mechanism

利用最小二乘法[25]解方程组，可获得尺度提升后各计算网格的等效渗透系数，由此可通过UTCHEM代码进一步计算地下水中NAPLs污染羽随时间变化的空间分布。

2 算例应用

2.1 算例概述

研究对象为二维非均质承压含水层，含水层面积为15 085 m2，厚度为5 m，地下水流方向从左向右，采用序贯高斯模拟生成二维非均质渗透率场[26-28]，渗透率场均值为10-10m2。含水层的有效孔隙度为0.35，水力梯度为0.001，纵向弥散度为1 m，横向弥散度为0.1 m。模型中涉及的液相参数：水的密度为1.0 g/cm3，PCE的密度为1.63 g/cm3，水的黏滞性为0.001 Pa·s，PCE的黏滞性为0.000 89 Pa·s，PCE与水的界面张力为0.045 N/m，PCE在水中的溶解度为240.0 mg/L。由于某种人为原因，造成PCE泄漏，并穿过弱透水层进入含水层。污染源分别有以下两种情形：

Case 1：单一污染源(单源)，PCE泄漏点(图2a)，泄漏量为1.0 m3/d。运移过程在时间上分为两个阶段：0～365 d的PCE泄露过程，366～730 d的PCE自然运移过程。

Case 2：双重污染源(二源)，PCE泄漏点(图2b)，泄漏量均为0.7 m3/d。运移过程与Case 1相同。

2.2 模型建立及尺度提升方案

根据参数先建立小尺度数值模型，横向划分为150个网格，纵向划分为85个网格，垂向为一层，则小尺度离散为12 750个单元格，每个单元格大小为x=1.0 m，y=1.0 m，这与微水试验测量的渗透系数尺度相似。平行于流动方向的边界为隔水边界，垂直于流动方向的边界为定水头边界。

大尺度离散采用非均匀离散，尺度提升方法运用算术平均法和拉普拉斯-外壳法。拉普拉斯-外壳法采用的是网格中心尺度提升，x轴方向外壳的大小取小尺度的20网格，y轴方向取小尺度的10网格。

图2 污染源模型的非均匀剖分Fig.2 Non-uniform block discretized model with polluted sources

对单一污染源污染点位置进行非均匀剖分(图2a)。算术平均尺度提升法将原始的渗透系数网格15 085(单元格大小11)提升到3 421，网格数从小尺度单元数12 750提升到大尺度单元数714。拉普拉斯-外壳法由于外壳不进行计算，因此将渗透系数网格提升到2 617，单元数为442。

对双重污染源两个污染点位置分别进行网格加密(图2b)，算术平均法将原始的渗透系数网格15 085(单元格大小11)尺度提升到3 825，从小尺度单元数12 750提升到大尺度单元数950，拉普拉斯-外壳法将网格提升到3 021，单元数为630。

3 结果与分析

3.1 单一污染源

图3为均质渗透系数场下，单源泄漏的PCE运行了2 a(730 d)后，在不同尺度下UTCHEM计算出的PCE运移结果，表1为污染羽的空间矩计算结果。由表1可知，在均质情况下，大尺度模型和小尺度模型得到污染羽的二阶矩存在一定误差，但其零阶矩和一阶矩误差很小，表明大尺度模型基本能再现小尺度模型精细刻画污染物的运移情况(图3)，以此可作为非均质情况的对照。

图4为单源情况下，不同渗透系数场中，PCE运行了2 a(730 d)后，UTCHEM根据不同网格剖分情况计算出的PCE运移结果，表2为污染羽的空间矩分析结果。大尺度模型对于含水层中污染物质量(零阶矩)的估算准确，相对误差绝对值均小于2%，但随着渗透系数对数方差的增大，误差增大。拉普拉斯-外壳法较算术平均法更为准确，且精确度受渗透系数对数方差的影响较小。对于质心位置(一阶矩)和污染羽在空间上的展布范围(二阶矩)，大尺度模型也能较好地刻画小尺度模型中的情形。拉普拉斯-外壳法与算术平均法的结果对比，在垂直水流方向上，两方法得到的效果接近；沿水流方向，拉普拉斯-外壳法能更好地刻画PCE的运移情况，各渗透系数场下，不仅质心位置更接近小尺度情况，而且污染物的最远运移距离也更接近。由于进行含水层污染物治理时，多选择在污染羽的上游和下游设井，因此，经过拉普拉斯-外壳法尺度提升后得到的大尺度模型能更好地为含水层修复提供参考。

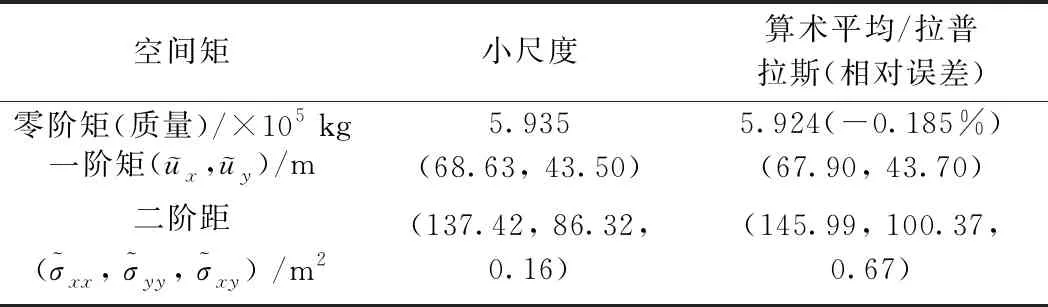
表1 单一污染源均质渗透系数场中污染羽在空间上的分布特征

图4 单一污染源非均质渗透系数场中PCE污染Fig.4 PCE saturation distribution in the heterogeneous permeability field under the single source situation

表2 单一污染源非均质渗透系数场中污染羽在空间上的分布特征

3.2 双重污染源

图5为均质渗透系数场下，双重污染源泄漏的PCE运行了2 a(730 d)后，在不同尺度下由UTCHEM模拟的PCE运移结果，表3为该污染羽的空间矩计算结果。由表3可知，同单一污染源情况一样，均质情况下，大尺度模型和小尺度模型得到的污染羽的二阶矩存在一定误差，但其零阶矩和一阶矩误差很小，表明二源情况下，大尺度模型也能基本再现小尺度模型精细刻画污染物的运移情况(图5)，以此可作为非均质情况的对照。

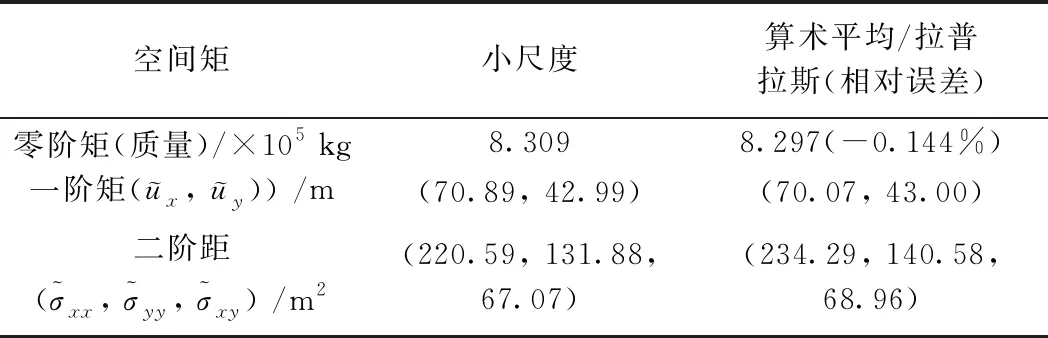
表3 双重污染源均质渗透系数场中污染羽在空间上的分布特征

图6为双重污染源不同渗透系数场下，PCE运行了2 a(730 d)后，UTCHEM根据不同的网格剖分情况计算出的PCE的运移结果，表4为该污染羽的空间矩分析结果。与单源情况相比，由于非均匀离散中，双重污染源细化的网格更多，因此在污染物质量估计方面，大尺度模型的准确度都较单源情况有所提升。双重污染源得到的分析结果与单源情况类似，进一步印证了拉普拉斯-外壳法的优越性。因此，在不同污染情况下，拉普拉斯-外壳法提升后的渗透系数场都能更好地等效小尺度渗透系数场情况。

3.3 计算效率

由于算术平均法和拉普拉斯-外壳法进行尺度提升的运算时间均极短，因此将UTCHEM模型的运行时间作为计算成本进行对比。本算例采用配置为Intel(R) Core(TM) i5处理器、3.2 GHz、3.4 G内存的计算机，具体运行时间见表5。

从表5中可以看出，尺度提升带来的计算时间减少是很可观的，并且小尺度模型计算时间越长，尺度提升后节约的计算时间越多。利用算术平均进行尺度提升后的模型计算时间为原模型的2.47%～4.28%，利用拉普拉斯-外壳法尺度提升后的模型计算时间为原模型的1.85%～3.45%。将二者的运行时间进行比较，所有情形下均是拉普拉斯-外壳法尺度提升后的模型计算效率更高，这是由于拉普拉斯-外壳法中外壳区域不用进行计算，因此拉普拉斯-外壳法得到的模型需要计算的网格数更少，从而具备更高的计算效率。计算效率极大的提高表明，渗透系数场的尺度提升对运移模型计算成本的降低是非常有效的。

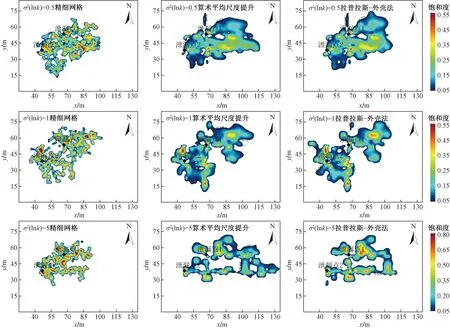
图6 双重污染源非均质渗透系数场中PCE污染Fig.6 PCE saturation distribution in the heterogeneous permeability field under the dual sources situation

表4 双重污染源非均质渗透系数场中污染羽在空间上的分布特征

4 结论

(1)零阶矩的计算结果表明，算术平均法和拉普拉斯-外壳法对渗透系数场进行尺度提升后得到的大尺度运移模型都能准确地估计含水层中污染物质量。相较而言，拉普拉斯-外壳法得到的结果更准确，且含水层非均质性越强，拉普拉斯-外壳法的优越性越明显。

表5 不同尺度提升方法的模型运行时间对比

注：a时间比：尺度提升后模型计算时间与尺度提升前模型计算时间的百分比。

(2)一阶矩和二阶矩的计算结果表明，在水流方向上，拉普拉斯-外壳法对质心位置的确定和污染羽的运移范围的计算更准确；在垂直于水流方向上，两种计算方法计算效果类似。因此，经过拉普拉斯-外壳法尺度提升后得到的运移模型刻画小尺度模型更准确，可更好地为后期的含水层污染修复提供参考。

(3)计算时间的对比结果表明，算术平均法和拉普拉斯-外壳法对渗透系数场进行尺度提升都能有效节省计算成本。