三阶幻方中的数字计算
蔺学益
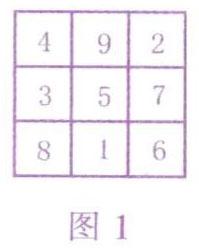

相传,大禹治水时,洛水中出现了一个“神龟”,其背上有美妙的图案,史称“洛书”,把“洛书”中的数填在对应的九宫格内,就是三阶幻方,
幻方是一种智力填数游戏,它是根据事先提供的数,运用逻辑推理的思维方法和排除法,把数填入空白的方格中.中国不仅拥有幻方的发明权,而且是对幻方进行深入研究的国家,
三阶幻方是最简单的幻方,是由1,2,3,4,5,6,7,8,9九个数组成的九宫格(如图1所示),其对角線、横行、纵列上三个数的和都为15,我们称这个最简单的幻方的幻和为15.中心数为5.
三阶幻方在中小学数学教科书中都有所体现.那么,这里的“其对角线、横行、纵列上三个数的和都为15”“中心数为5”隐含着怎样的数学计算呢?
我们先来说“其对角线、横行、纵列上三个数的和都为15”中的“和为15”
如图2所示,我们设每个格子的未知数分别为x1至x9,从中选取横行(或者纵列)来分析,那么有:
x1+x2+x3=S;
x4+x5+x6=S;
x7+x8+x9=S.
三个式子相加,则有:
3S=x1 +x2+x3+x4+x5+x6+x7+x8+x9.
因为xl至x9 -定是1至9这九个数,所以x1+x2+x3+x4+x5+x6+x7+x8+x9=45.
由3S=45.得到S=15.
由每个横行上三个数的和都是15,同理可推得每个纵列和对角线上三个数的和都是15.
再来说“中心数为5”,我们选择中间的横行、中间的纵列和两个对角线上的三个数之和,由于S=15,则有:
x4+x5 +x6 =15,x2 +x5 +x8=15,x1+x5 +x9 =15,X3+X5+X7=15.
四个式子相加,则有:
x1+x2+x3+x4+x5+x 6+x7+x8+x9+3x5=60.
故45+3xs=60,求得x5=5,也就是说“中心数为5”.
这样我们就解释了三阶幻方中的两个值的由来,下面,就可以进行填写这九个数值的操作了,
利用以上两个填写依据,我们来看和为15的八个(三个横行、三个纵列、两个对角线)等式:
1+5+9=15,2+5+8=15;
3+5+7=15,4+5+6=15;
1+6+8=15,2+4+9=15;
2+6+7=15. 3+4+8=15.
这八个等式会出现在三阶幻方中(也只有这八个等式),我们会再次发现有趣的事实:“5”出现了四次,而在九个格子中只有中间格被用了四次,因此“5”就必须在幻方最中间的位置.这样,就再次解释了“中心数为5”的缘由.
另外,“2”“4”“6”“8”四个数在等式中都出现了三次,而在九个格子中只有四个角的格子被用了三次,因此这四个数应放在幻方的四个角中.当然,“2”和“8”在同一等式中,“4”和“6”在同一等式中.
同样地,“1”“3”“7”“9”四个数在等式中都出现了两次,只能将这四个数放在幻方的靠边的四个中间格子中.“1”和“9”在同一等式中,“3”和“7”在同一等式中.
综合以上解释,三阶幻方要满足横行、纵列和对角线上三个数之和等于15,只能将“5”放在最中间的方格中,将“2”“4”“6”“8”放在四个角中,将“1”“3”“7”“9”放在靠边的四个中间格子中.
有了以上更清晰的数的位置填写要求,在兼顾三数之和为15的情况下,会得到八种不同的三阶幻方填法.有兴趣的同学可以自己试着填一下,
通过对三阶幻方的数学计算与填写解释,大家是不是感受到了幻方的魅力呢?探究幻方的奥秘是一件既有趣又有意义的事情,能让大家对数学产生更浓厚的学习兴趣,这也许就是幻方的迷人之所在吧!
- 中学生数理化·七年级数学人教版的其它文章
- 持之以恒的王羲之
- 外角和为360°
- 把握相交与平行
- “相交线与平行线”学习指导
- 观三线 抓特点 辨八角
- 拓展探究 培养思维

