基于粒子群改进的自适应核密度估计算法的江苏省地面气温分析

叶小岭， 陈 昕， 熊 雄， 阚亚进， 王佐鹏

(1.南京信息工程大学自动化学院， 南京 210044； 2.南京信息工程大学气象灾害预报预警与评估协同创新中心， 南京 210044)

近年来全球变暖趋势愈发明显，气温变化给社会生产生活带来了严重的影响[1-2]，对于气温变化有效的研究可以为气候预测、灾害预警等方面提供科学的帮助，为此中外学者进行了许多有意义的研究[3-4]。就中国而言，对全国气候变化、特殊地区(高原和盆地等)气温以及极端气温变化特征的研究取得了许多成果，如谢星旸等[5]与彭凯等[6]分别对中国的冬季与春季气温变化规律进行了研究与分析；而在特殊地形如青藏高原、新疆塔里木盆地等不同地区，朱伊等[7]与郑奕等[8]分别对此进行了温度的时空变化研究；此外，对现代气象灾害预警具有重大意义的极端气温变化方面，也有许多专家进行研究，如高丽等[9]基于美国国家环境预报中心-全球集合预报系统(NCEP-GEFS)资料对中国极端气温变化特征进行了分析；江晓菲等[10]则模拟分析了中国未来极端气温变化的概率估计及其不确定性。中国学者不仅对全国、特殊地区抑或是冬季、春季、极端气温等较大较特殊的方面研究较为充分，对小地区或者特例地区的细致研究方面也有涉及，如李叶妮[11]等对营口地区的气温从多时间尺度的角度进行了研究与分析。

同时，在方法层面上，对于传统的相关性分析、回归分析、Mann-Kendall趋势和突变检验、经验正交函数分解(empirical orthogonal function，EOF)等方法，宋伟等[12]对此做了很好的应用，成功分析了中国东部冬季与北极近地面温度变化的联系；尹义星等[13]则对中国江苏省的气温变化趋势以及极端气温做了相应的研究。与此同时，国外的学者如Hannachi等[14]、Worku等[15]对EOF算法及Mann-Kendall检验方法进行了改进，且对研究对象的选取也进行了新的尝试，成功地将传统方法改进并应用到全球范围内的气温分析当中去。

经探讨存在以下两个问题：①分析方法多选取线性趋势分析、相关系数分析、Mann-Kendall检验及EOF等方法，在方法层面仍有改进空间；②由于气温分析多在年时间尺度下进行，分析面不够细致，对季度、月度、日夜时间尺度下的气温变化，如区域性与季节性差异[16-17]等，可以进行深层次的研究。因此现引入核密度估计算法并采用自适应以及粒子群算法加以改进，研究该算法在不同时间尺度下的灵敏度，并将该算法应用于区域的气温分析，期望得到更好更精细的效果，为分析气温时空变化以及影响特征作为参考。

1 资料选取

所用的数据来源于国家气象中心，包含江苏省13个城市75个地区的地面观测站1951—2009年地面定时(02:00、08:00、14:00、20:00)观测资料(6 h气温)，已经过传统质量控制，明显的粗大误差已被剔除。经筛选后选取1961—2008年江苏省12个城市：徐州(站号：58027)、宿迁(站号：58131)、连云港(站号：58044)、淮安(站号：58141)、扬州(站号：58245)、南京(站号：58238)、镇江(站号：58248)、常州(站号：58343)、盐城(站号：58154)、无锡(站号：58354)、苏州(站号：58349)、南通(站号：58259)的气温6 h数据以及月平均数据作为基础资料进行数据预处理，取08：00与14：00气温的平均值作为日均温，取20：00与02：00气温的平均值作为夜均温，取12月—次年2月为冬季度均温，3—5月为春季度均温，6—8月为夏季度均温，9—11月为秋季度均温。

2 分析方法

2.1 核密度估计

核密度估计(kernel density estimation，KDE)算法由Rosenblatt[18]和Parzen[19]提出。与参数估计方法相比，其优点在于对观测资料的分布不附加任何假定，也不需要了解分布的先验知识，利用样本数据直接得到函数的密度估计，从而对数据进行可视化的解释。

假设(x1,x2,…,xn)为单站点下n个时间观测样本变量，则密度函数公式为

(1)

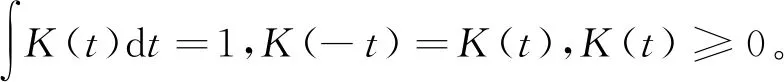
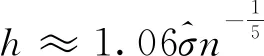
(2)

2.2 粒子群优化的自适应核密度估计

由于固定窗宽不能够有效反映数据的稀疏程度带来的影响，因此需要引用自适应算法(adaptive algorithm)进行改进，同时本文在自适应算法改进的基础上进一步提出粒子群(particle swarm optimization，PSO)优化的方法，最终改进后的自适应核密度估计(adaptive kernel density estimation algorithm improved by particle swarm optimization， PA-KDE)算法公式为

(3)

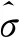
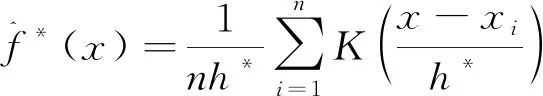
(4)

结合窗宽系数λ代入式(4)即可得到式(3)，下面围绕改进后得到的PA-KDE算法进行相应的灵敏度试验与分析以及算法在江苏地区的应用与分析，算法的流程如图1所示。

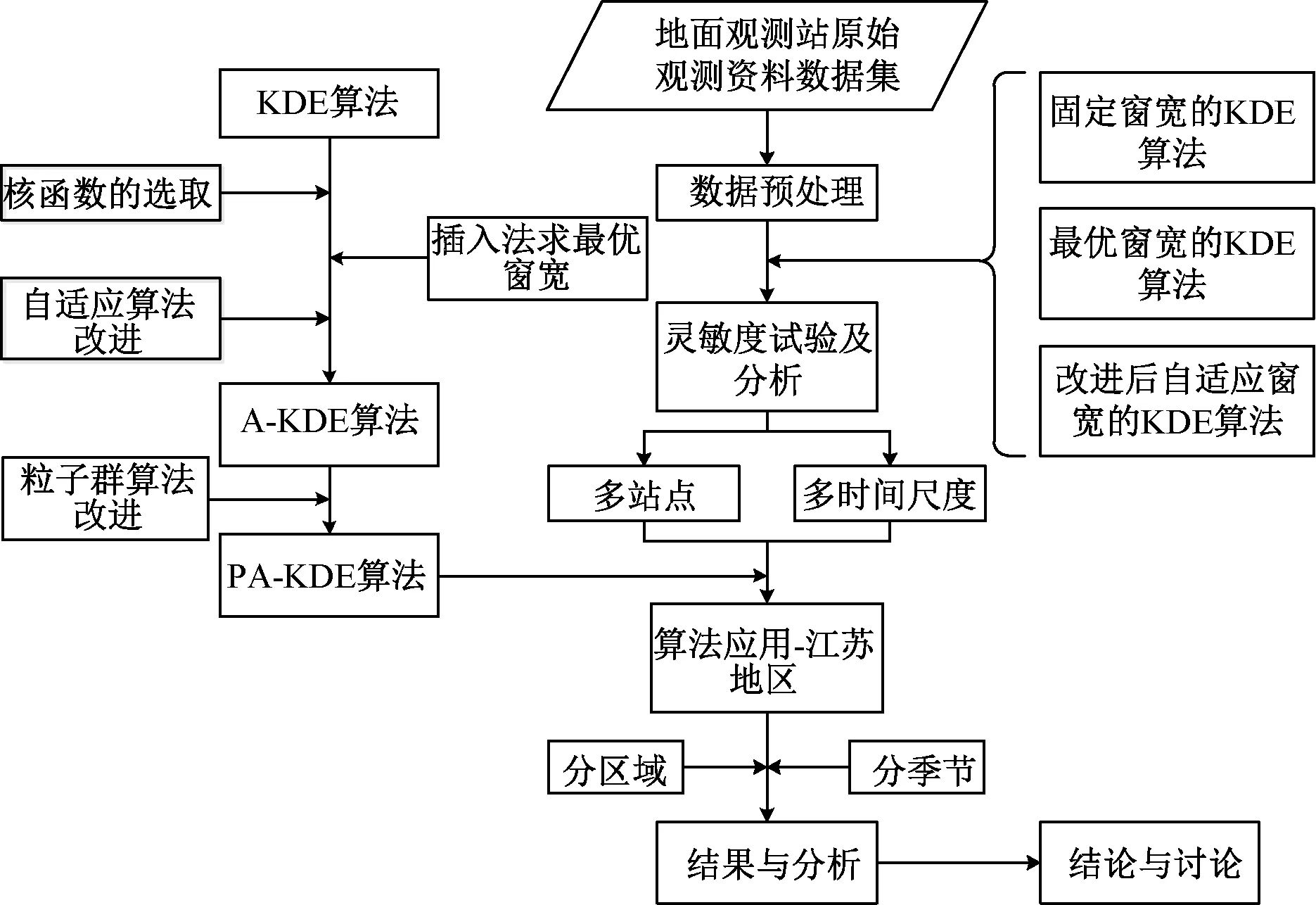
图1 算法改进及应用流程图Fig.1 Flow chart of algorithm improvement and application

依据图1所示，左边由经典的KDE算法按照所提出的改进方法得到新的PA-KDE算法，在此基础上利用固定窗宽、最优窗宽以及改进后的自适应窗宽下的三种KDE算法分多站点以及多时间尺度地进行灵敏度分析，最后结合新的PA-KDE算法与江苏地区预处理后的地面气温观测资料分区域与季节对结果进行分析，并进行相应的结论总结与讨论。

3 试验结果与分析

3.1 PA-KDE算法的灵敏度分析

为测试PA-KDE算法在多站点下对不同时间尺度的气温数据的灵敏度，由于窗宽对于灵敏度的影响最为关键，选取改进前KDE算法中的固定窗宽(fixed h，F_H)、最优窗宽(optimal h，O_H)与改进后PA-KDE算法中的自适应窗宽(adaptive h，A_H)进行对比试验，依次进行季度均温下不同站点(根据试验结果，选取徐州、连云港、南京、南通四站进行展示，如图2所示)的试验以及多时间尺度(季度、月度以及日夜)下单个站点(以徐州为例，如图3所示)的均温对比试验，并利用平均绝对误差(mean absolute error，MAE)、均方根误差(root mean square error，RMSE)、纳什系数(Nash-Sutcliffe model efficiency coefficient，NSC)和观察者一致性(interobserver，IOA)指标对灵敏度进行评价。MAE与RMSE表示预测精度，值越小表示精度越高；NSC和IOA用来度量拟合优度，值越大且越接近1表示拟合优度越高。

分析图2可得，在MAE与RMSE指标下A_H算法得出的值最小，O_H算法得出的值最大，表明O_H算法在预测精度上不适用于江苏省地面气温观测资料季度均温；在NSC与IOA指标下可以看出A_H算法得出的值最大且接近1，O_H算法得出的值最小，表明在拟合优度上，O_H算法也不适用；而A_H算法无论是预测精度还是拟合优度都好于其他两种算法，F_H算法效果介于两者之间，且固定窗宽算法没有普适性，因此三种算法的试验效果为A_H> F_H> O_H。

图2 季度尺度下三种算法在四站点的指标对比Fig.2 Numerical comparison with indicators of three algorithms in the four city stations at the quarterly time scale

进一步进行灵敏度分析，分析图3可得，在MAE与RMSE指标下，A_H算法得出的值最小，O_H算法得出的值最大，且随着时间尺度变小越来越接近，表明在预测精度上A_H算法效果最优，F_H与O_H算法在月度及日夜时间尺度下也可行，在季度时间尺度下的效果不佳；在NSC与IOA指标下A_H算法得出的值最大，O_H算法得出的值最小，且同样随时间尺度变小而越来越接近，表明在拟合优度上也是A_H算法效果最优，而F_H与O_H算法仅在日夜时间尺度下可行，在季度及月度时间尺度下的效果均不佳；整体看来三种算法效果A_H> F_H> O_H，且A_H算法的可行性与普适性最好。

根据试验结果，江苏省12个站点的指标信息综合出的结论一致，因此提出徐州站点下不同时间尺度、不同算法的四项指标数值信息作为参考，如表1所示。可以看出改进后的PA-KDE算法(使用自适应窗宽A_H)就预测精度与拟合优度方面在多站点与多尺度下拥有更良好的效果，对不同时间尺度以及不同站点的气温数据有着很好的灵敏度，对于深入分析地面气温观测资料在多时间尺度下的时空变化特征有着很好的帮助。

图3 不同时间尺度下三种算法在徐州站指标对比Fig.3 Numerical comparison with indicators of three algorithms in Xuzhou station at different time scales

表1 不同时间尺度下三种算法在徐州站点的各指标数值

3.2 PA-KDE算法案例应用与分析

根据上述试验结果，采用PA-KDE算法对江苏省12市地面气温观测资料进行季度、日、夜尺度下的试验，结合不同影响因子对图4～图6的时空变化特征进行分析。相比于现有的气温分析方法，PA-KDE算法可以包含更多的信息，因此需要分区域与季节的分析地面气温观测资料在多时间尺度下的时空变化特征(趋势、概率特征等)以及不同影响因子(气候、地理位置、海洋调节等)的影响，其中曲线纵轴的数值代表了对应气温值的概率特征，曲线在横轴上的宽度代表了极端气温的极值，而曲线的陡峭程度则可以显示出气温变化的趋势。图4～图6为试验结果曲线图。

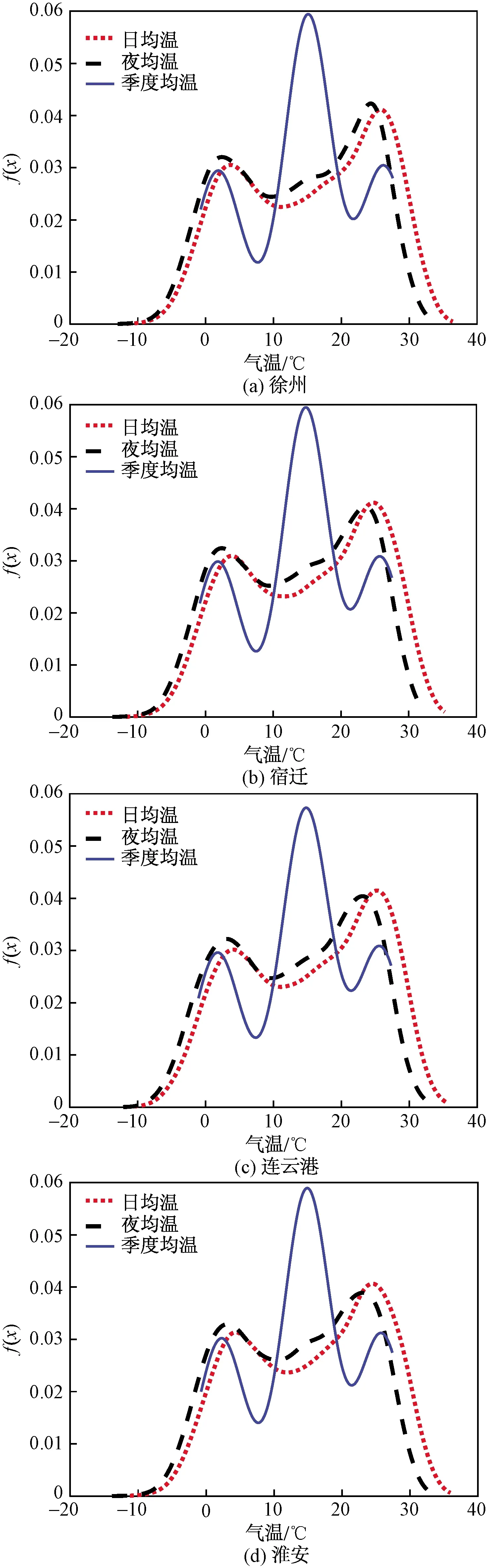
图4 徐州、宿迁、连云港、淮安站点在PA-KDE 下的季度、日、夜均温曲线Fig.4 Curve of quarterly mean temperature, daily mean temperature and nightly mean temperature under the PA-KDE in Xuzhou, Suqian, Lianyungang, Huaian

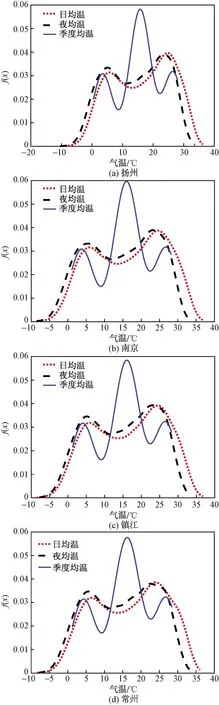
图5 扬州、南京、镇江、常州站点在PA-KDE 下的季度、日、夜均温曲线Fig.5 Curve of quarterly mean temperature, daily mean temperature and nightly mean temperature under the PA-KDE in Yangzhou, Nanjing, Zhenjiang, Changzhou

图6 盐城、无锡、苏州、南通站点在PA-KDE 下的季度、日、夜均温曲线Fig.6 Curve of quarterly mean temperature, daily mean temperature and nightly mean temperature under the PA-KDE in Yancheng, Wuxi, Suzhou, Nantong

3.2.1 季度时间尺度下的气温分析

根据季度均温曲线的三个峰值，假设以25 ℃以上代表夏季，15 ℃左右代表春秋季，5 ℃以下代表冬季进行分析，其中曲线整体越往右代表均温越高，f(x)的值越大代表均温持续时间越长。

季度均温曲线图分区域分析如下：根据季度均温曲线的变化，将江苏地区分为三大区域，分别为图4四市所构成的江苏北部区域、图5四市所构成的江苏西南内陆区域以及图6四市所构成的江苏东部及东南沿海区域。根据第一区域可以看出春秋季的f(x)值接近0.06，且随着位置偏南以及偏东会有所降低，冬季与夏季的f(x)值在0.03左右，对比发现徐州与宿迁的四季均温时长接近，淮安春秋季均温时长稍短，连云港春秋季的时长更短，原因分析：虽然四市同属季风气候，但是徐州与宿迁为温带气候，而淮安与连云港为温带与亚热带过渡气候，且由于连云港靠海，还受到海洋作用的影响。第二区域相对于第一区域而言，春秋季的f(x)值降低，冬季与夏季的f(x)值升高，且整体季度均温曲线往右偏移，其中南京除了曲线整体往右偏移外，整体曲线的频次数值反而与第一区域近似。原因分析：该区域相对于第一区域整体偏南，属于江苏的内陆地区，同时南京作为经济较为发达的省会城市，经济环境对其均温的升高也造成了一定影响。第三区域相比于前两个区域而言，春秋季的f(x)值进一步降低，冬季与夏季的f(x)值进一步升高，且整体均温更加往右偏移，原因分析：该区域相较于前两个区域偏东及东南沿海，且气候以亚热带季风气候与海洋气候为主，其中盐城由于地理位置偏北与海洋作用的影响，使得其整体均温又向左偏移了回去。

结合图7站点分布综合分析：气候的影响大于位置带来的影响，位置越偏东南，春秋季均温时长越短，冬夏季均温时长越长，且整体均温越高，温度变化越稳定，海洋调节作用一定程度上弥补了位置偏东南带来的影响。

图7 江苏省12市站点分布Fig.7 Distribution of 12 cities in Jiangsu Province

3.2.2 日、夜时间尺度下的气温分析

日、夜均温曲线图分析如下，日、夜均温数据量较大且f(x)曲线在横轴上较长，假设以25 ℃以上代表夏季，15 ℃左右代表春秋季，5 ℃以下代表冬季，为了便于交叉验证，将曲线分季节进行分析。

日、夜均温夏季曲线部分有四种情形：①日间均温曲线位于夜间均温曲线偏右上方，图4宿迁、连云港、淮安三市日间均温的f(x)值比夜间均温略高，图6(a)盐城则高出许多，原因分析：以上四市位于江苏省北部，其中盐城受海洋调节作用影响，该区域日均温高于夜均温且日间的高温持续时间也比夜间长。②日间均温曲线位于夜间均温曲线右下方，仅图4(a)徐州市呈现这种情况，原因分析：徐州位于江苏省最西北部，且属于温带季风气候，该市日均温略高于夜均温但是日间高温时长低于夜间。③日间均温曲线在夜间均温曲线的右边，f(x)值大小大致持平，图5扬州、南京、镇江、常州四市均温趋势如此，原因分析：以上四市位于江苏省西南及中部，相较于前两种情形位置偏南，日均温时长有所降低。④日间均温曲线高于夜间均温曲线且夜间均温曲线有波动，图6中无锡、苏州、南通三市均温趋势如此，原因分析：以上三市位于东南沿海区域，均属于亚热带季风气候与海洋气候，相较于第三种情况，以上三市夜间气温有所降低且波动，海洋调节对夜间气温影响较大，另外，随着气候从温带季风向亚热带季风以及海洋气候变化的同时，均温曲线整体偏右移。

结合图7站点分布综合分析：气候影响均温的变化趋势，位置则影响均温的持续时长，海洋调节则会同时提高日均温与其时长，会降低夜均温且不稳定，在位置一致的情况下，海洋性气候与季风性气候带来的影响差别不大。

日、夜均温春秋季曲线图分两种情形：①日均温与夜均温之间曲线距离相差较大，代表夜均温持续时长高于日均温；②日均温与夜均温之间曲线距离相近，呈现日、夜均温持续时长趋于一致；结合图4～图6位置与气候特征分析：海洋调节的影响会使得春秋季夜均温持续时长增加，位置上越偏南，日夜均温曲线之间的差距越大，夜均温持续时长比日均温越高，海洋调节为春秋季均温划分的重要因素，其次各个区域间南北位置不同带来差异，越靠近东南沿海，曲线差距越大。

日、夜均温冬季曲线图变化与春秋季相近，也分为两种情形：①夜均温曲线远高于日均温，这也符合冬季昼短夜长的现状；②夜间均温曲线略高于日均温且较为贴近；结合图4～图6站点分布综合分析：位置为冬季均温产生差异的主要原因，位置越偏西北，冬季夜均温持续时间越长，反之，越偏东南，冬季夜均温持续时间越短，但始终高于日均温，海洋调节作用下会使得冬季均温下降。

4 结论

引入统计学概率预测中的非参数核密度估计方法并采用自适应与粒子群算法加以改进，对江苏省12个站点的地面气温观测资料分别进行了试验并加以分析，可以得到以下结论。

(1)改进的PA_KDE算法在季度、月度、日夜时间尺度下均拥有良好的预测精度与拟合优度，拥有很好的可行性与普适性，为传统方法开拓了新的时间尺度分析路径。

(2) PA_KDE方法在江苏每一个站点的试验结果都包含大量可供分析的信息，可以更为有效地深入分析地面气温观测资料。该方案为讨论气温时空变化以及影响特征提供借鉴。

(3)分析所得不同影响因子间存在的联系、协同关系，值得后续气象研究的深入。仅选择了江苏地区气温资料的分析，该方法还可以借鉴衍生到其他地区以及非气象资料的分析中去。