单筒式磁流变减振器多目标优化与试验研究

张丽霞, 郑超艺, 潘福全, 林炳钦

(1.青岛理工大学机械与汽车工程学院， 青岛 266520; 2.清华大学车辆与运载学院， 北京 100084; 3.科马智能悬架技术(青岛)有限公司， 青岛 266520)

车辆悬架系统能有效隔离路面引起的冲击和振动并起支撑作用，以满足车辆的乘坐舒适性和行驶安全性。与传统的被动悬架相比较，半主动悬架系统能实时匹配悬架所需的阻尼力要求，根据实际情况进行调整[1]。作为半主动悬架系统执行元件的磁流变减振器，因其结构简单、阻尼力可控、输出阻尼力大、响应速度快、动力可调系数大、控制相对简单、能耗低等优点，成为目前半主动悬架的主要研究方向。美国马里兰大学[2]深入研究磁流变减振器的设计理论，研发了单筒充气补偿式磁流变减振器。圣母大学[3]研发了类似的磁流变减振器，并进行试验研究，为了提高输出阻尼力的数值，可以改变工作缸的材料电磁纯铁，以提升整个磁路的导磁性能。廖昌荣[4]、余淼[5]依据磁流变液的宾汉流体模型，设计研发了混合工作模式的磁流变减振器及整套控制系统，并成功应用于长安微型汽车。张琳[6-7]设计了多级线圈式磁流变减振器，相比于单级线圈式常规型磁流变减振器，提高了系统的动态性能。Zhao等[8]利用多目标优化软件以响应时间和阻尼力为优化目标进行减振器结构参数和阻尼力为优化目标进行减振器结构参数优化。Mei等[9]、瞿伟廉等[10]对减振器磁路部分以相关结构参数为变量进行优化设计。杨文荣等[11]采用参数化编程语言建立磁流变减振器磁路部分模型进行结构参数优化设计。

磁流变减振器(magneto-rheological damper，MRD)的设计是一个非线性多目标优化问题，合理设计其结构参数才能达到最佳性能。尽管人们对磁流变减振器的结构优化做了大量研究，但传统的大多数设计只考虑单目标因素，并不能从根本上提高其性能要求，而且设计过程烦琐。另外，在优化过程中针对磁流变液工作时的特性只作预常数处理，并没有在线反馈各结构参数对磁流变液产生的磁感应强度的影响，并不能实现对磁流变减振器全面优化设计。

以某一车型的后悬架减振器基本性能要求和结构为设计条件，以阻尼力和动力可调系数为优化目标，基于Pareto集和Bingham模型多目标优化方法探究各设计变量对优化目标的设计敏感性，搭建非线性多目标优化模型和实现算法进行磁流变减振器结构优化设计，通过试制原理样机进行试验分析研究，验证优化设计的磁流变减振器满足实际的应用需求。

1 磁流变减振器阻尼力与动力可调系数计算

磁流变液在无外加磁场的情况下表现为Newton流体特性，在外加磁场作用下瞬间从Newton流体转变为Bingham流体特征。依据Bingham流体本构方程[12]，有

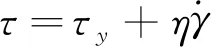
(1)

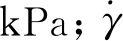
由此可以得到在流动工作模式下磁流变减振器的阻尼力[13]为

(2)

式(2)中：l1为活塞阻尼通道有效长度，mm；l2为线圈槽的宽度，mm；h为活塞与活塞外套间的阻尼通道间隙，mm；Ap为活塞有效面积，Ap=π(D2-d2)/4，D为活塞外径，mm；d为活塞杆直径，mm；v为活塞相对于缸体的运动速度，m/s；sgn(v)为符号函数。

所以相应的磁流变减振器动力可调系数可表示为

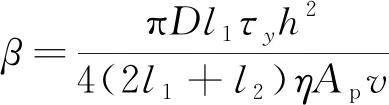
(3)

2 磁流变减振器优化设计

2.1 设计目标

在进行磁流变减振器设计时，既要考虑其减振性能又必须考虑汽车操纵稳定性及舒适性等性能。当汽车行驶在不同工况时，所提供的阻尼力能够满足基本要求，并期望提供的阻尼力可调范围越大越好。为了进行有效的半主动控制，要求减振器响应时间尽可能短，同时要求其耗能小，从而减小线圈发热，保证磁流变减振器在稳定的范围内工作。然而需要同时满足以上要求很难实现，因为各个性能要求之间是相互约束的，为了尽可能满足各性能要求就必须综合考虑减振器的结构参数，根据多目标设计理念进行设计，选择合适的结构参数[14]。基于NSGA-Ⅱ遗传算法，以阻尼力和动力可调系数为优化目标，分析各设计变量对阻尼力和动力可调系数的影响并通过试验进行验证。具体优化流程如图1所示。

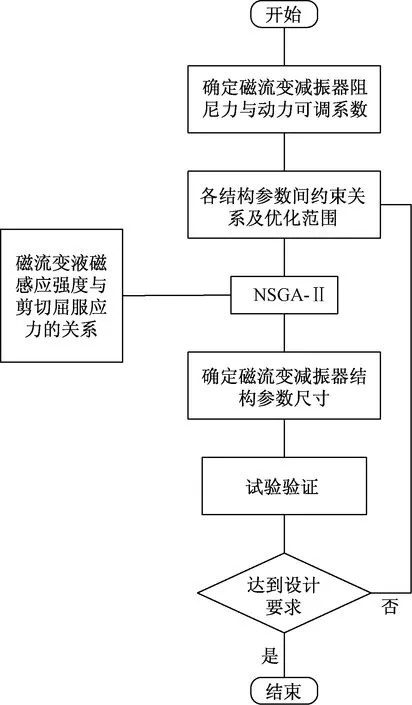
图1 磁流变减振器优化设计流程Fig.1 The optimized design flow of MRD

2.2 优化变量

由阻尼力公式可知，进行磁流变减振器结构设计应该考虑到以下几个变量：阻尼通道间隙h、阻尼通道有效区域长度l1及非有效区域长度即线圈槽的宽度l2、活塞杆半径r、活塞杆线圈半径差T1、线圈槽深度T2、活塞外套厚度w。具体结构优化设计尺寸变量如图2所示。参考磁流变减振器相关设计要求，各个结构参数优化范围如表1所示。

图2 结构优化尺寸参数Fig.2 The structural optimization dimension parameters

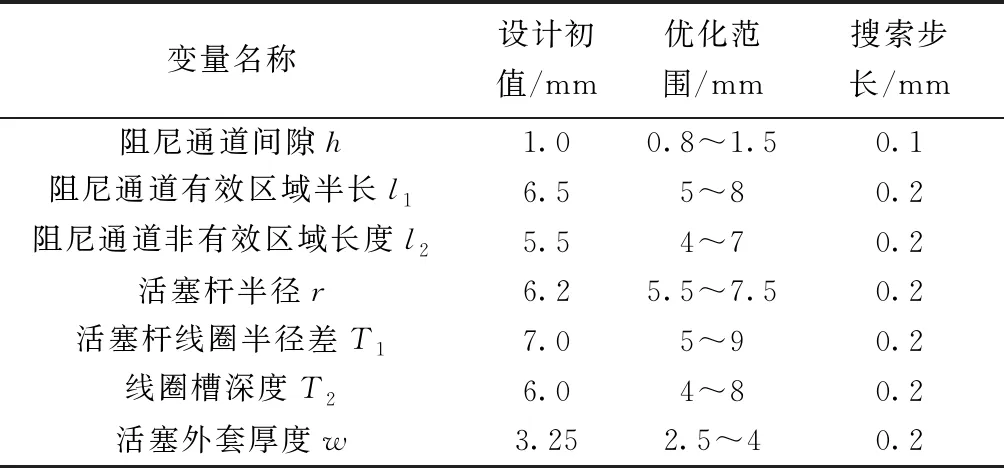
表1 优化变量Table 1 The optimization variables

2.3 约束条件

(1)由磁流变减振器阻尼力计算公式可以得到黏滞阻尼力和库仑力约束。

黏滞阻尼力：

(4)

库仑力：

(5)

(2)按照以往的设计经验，一般规定活塞杆半径为工作缸内径的0.3～0.35倍，所以此约束为

(6)

(3)为了满足安装尺寸要求和防止减振器体积过大，需要对磁流变减振器的活塞体积进行约束：

V=π(r+T1+T2+h+w)2(4l1+2l2)

(7)

各阻尼力大小依据磁流变减振器的工作要求进行约束，各材料磁感应强度依据各材料的磁饱和强度进行约束，依据《汽车筒式减振器尺寸系列及技术条件》(QC/T 491—1999)对各结构参数进行约束，可得各状态变量的优化范围如表2所示。

表2 状态变量优化范围Table 2 The optimal range of state variables

2.4 目标函数

依据2.1节的设计目标，为了使设计的磁流变减振器兼顾各性能要求，设计以下两个目标函数，即工作电流最大时磁流变减振器所能提供的最大阻尼力F和最大动力可调系数β。阻尼力与动力可调系数计算公式如式(8)、式(9)所示。

阻尼力：

F=Fη+Fτ

(8)

动力可调系数：

(9)

2.5 优化求解

利用多目标优化软件modeFRONTIER强大的CAE流程自动化及软件集成平台，与数值计算软件MATLAB相结合，采用modeFRONTIER自身集成的优化算法搭建磁流变减振器多目标优化模型，如图3所示。其中，通过modeFRONTIER定义各设计变量并依据设计经验给定初始设计值，然后赋予MATLAB软件中表征阻尼力和动力可调系数等计算公式的m文件，仿真优化后得到最大阻尼力和最大动力可调系数值。

图3 磁流变减振器多目标优化模型Fig.3 The multi-objective optimization model of MRD

依据设计目标设定100组初始优化变量，按照表1中各变量的取值范围和搜索步长进行参量设置，结合表2的状态变量优化范围和减振器的性能要求设定约束条件和优化范围。选择基于遗传算法的多目标优化算法——NSGA-Ⅱ，其中遗传代数设置为100代，交叉概率为0.9，实数编码向量的变异概率和二进制字符串的变异概率均设为0.5，选中自动缩放突变概率，实数编码交叉和突变分布指数均设置为20，选择“simple”二进制编码变量的交叉类型，最后设置50个随机发生器种子设置完毕后进行结构参数多目标优化计算。经过10 000次迭代后，从Pareto前沿解集(图4)中可以看出采用Bingham模型进行优化设计的磁流变减振器最大阻尼力与最大动力可调系数值成反比，增大或减小最大阻尼力的值时，最大动力可调系数减小或增大，所以需要根据实际和设计需求选择合适的优化解。

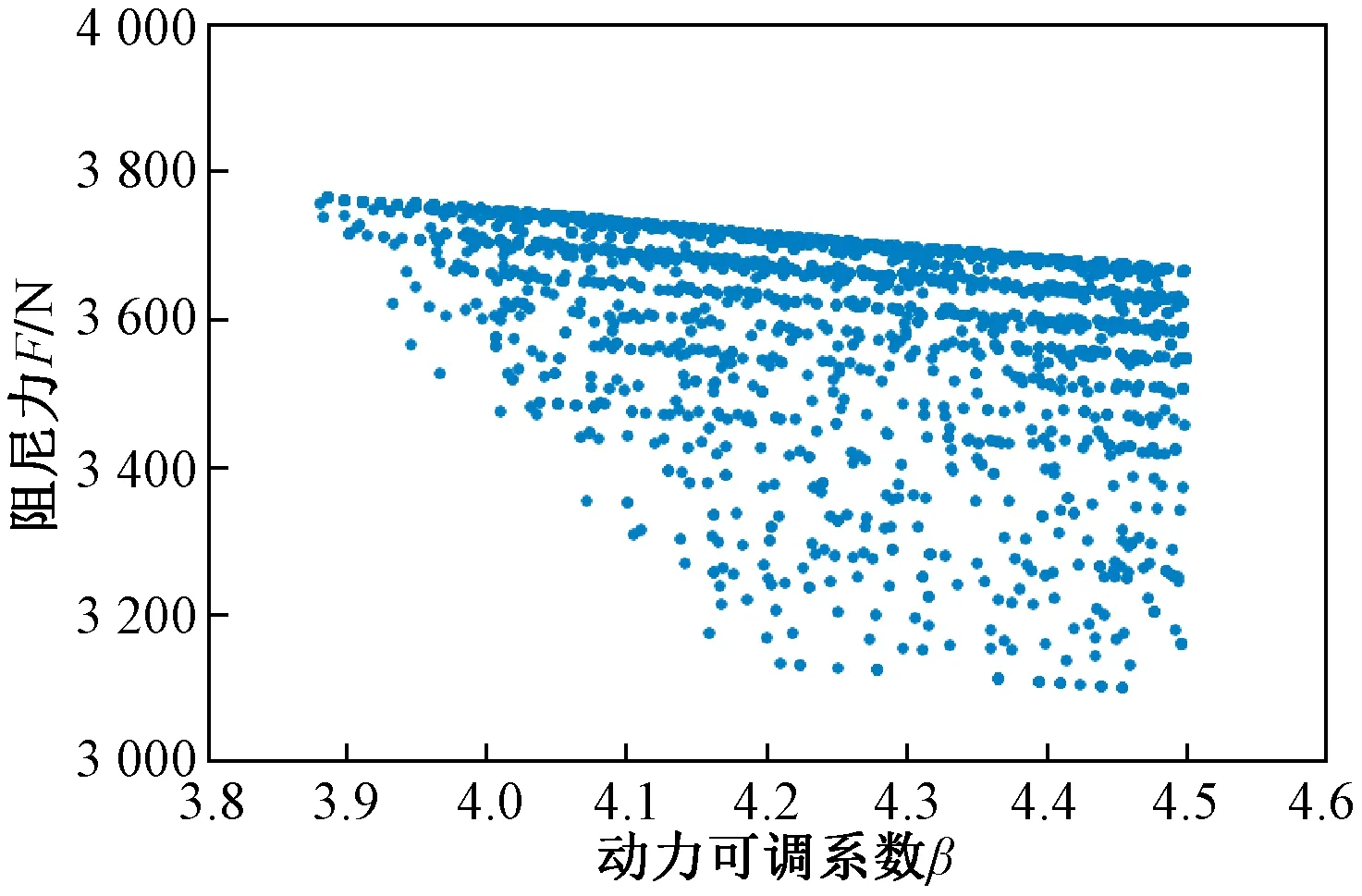
图4 Pareto解集Fig.4 The Pareto solution set

如图5所示，从优化变量与优化目标的相关系数矩阵可以看出，在各个变量优化范围内，7个变量对两个优化目标的设计敏感性。通过分析可以得到：对最大阻尼力Fmax影响最大的两个变量因素为线圈槽深度T2和阻尼通道有效区域半长l1，相关系数分别为0.053和0.496，即均为正相关关系；影响最大动力可调系数βmax的设计因素为阻尼通道间隙h和阻尼通道非有效区域长度l2，相关系数分别为0.960和-0.150，即分别为正相关和负相关关系，而阻尼通道间隙h对最大阻尼力Fmax的影响为负相关关系，相关系数为-0.434，所以阻尼通道间隙h的选择对两个优化目标取值至关重要。最大阻尼力Fmax与最大动力可调系数βmax为负相关关系，相关系数高达-0.517，所以如果两优化目标同时取得较大值，需要对设计变量进行折中选择。通过对10 000组优化结果进行分析，当需要同时满足最大阻尼力Fmax与最大动力可调系数βmax时，对于各设计变量的取值可以按照以下几个原则：①阻尼通道间隙h的取值为0.8～1.0 mm；②在满足线圈电阻和匝数布线要求的前提下，尽可能加大阻尼通道有效区域半长l1的取值；③为了提高动力可调系数βmax，尽量减小活塞外套厚度w，但为了后期磁路仿真计算不出现活塞外套平均磁感应强度值大于其材料本身磁饱和值，其值的选择应该大于活塞杆线圈半径差T1的一半；④在满足设计目标的前提下，为了节约制造成本，应尽量减小减振器尺寸，即活塞杆线圈半径差T1尽量小；⑤线圈槽尺寸取值尽可能小以缩短响应时间和提高活塞的结构强度。

因此依据分析结果，可以从图4中的3 814组Pareto解集中选取一组最优解，其序号为6 605，各参数如表3所示。

图5 相关系数矩阵Fig.5 The correlation coefficient matrix

表3 Pareto最优解Table 3 The Pareto optimal solution

3 磁流变减振器试验验证

3.1 试制磁流变减振器原理样机

为验证设计的磁流变减振器性能是否满足要求，需要进行磁流变减振器工作特性试验，测试磁流变减振器在不同电流和速度下的阻尼力大小。根据研究在给定多个约束条件和目标函数等条件下多目标优化设计得到的最优解，确定磁流变减振器活塞总成各结构参数，如表4所示。

表4 优化前后的设计参数Table 4 The design parameters before and after optimization

按照表4优化前后的磁流变减振器设计方案选择各部分结构材料并试制6支原理样机，其中阻尼通道用的磁流变液是清华大学车辆与运载学院智能悬架与轮胎课题组研制的6-5#-1型磁流变液。6支原理样机中标记01～03号为优化前尺寸，标记04～06号为优化后尺寸，如图6所示为06号磁流变减振器原理样机。

图6 06号磁流变减振器原理样机Fig.6 The principle prototype of No.06 MRD

3.2 磁流变减振器试验方案

减振器示功机是减振器行业里常用的一种设备，适用于对减振器进行示功特性及耐久性疲劳试验等。试验在科马智能悬架技术(青岛)有限公司试验中心的PWS-16电液伺服减振器综合性能试验台上进行测试(图7)，该综合性能试验台主要由测试设备、被测试对象和外接电源组成。由测试设备自带的力传感器采集力值信号，而试验速度和行程则通过其自带的位移传感器实现[15]。

图7 PWS-16电液伺服减振器综合性能试验台Fig.7 PWS-16 electro-hydraulic servo damper comprehensive performance test bench

依据国家对车用减振器的相关试验准则《汽车筒式减振器尺寸系列及技术条件》(QC/T491—1999)和《汽车筒式减振器台架试验方法》(QC/T545—1999)，采用PWS-16电液伺服减振器综合性能试验台对加工的磁流变减振器原理样机进行相关试验，具体试验条件设定如下。

①测试前，减振器在(23±3)℃的温度下至少存放6 h；②减振器测试振幅为±50 mm(行程100 mm)，简谐运动；③试验初始位置：大致在减振器的行程中间部分；④试验方向：铅垂方向；⑤励磁电流范围：0～3 A，测试电流分别为0、0.5、1.0、1.5、2.0、2.5、3.0、2.5-、2.0-、1.5-、1.0-、0.5-、0-A等，其中“-”表示电流下降阶段；⑥测试速度：0.050、0.131、0.262、0.393、0.524、0.750 m/s等，实际测试过程中速度会略有变化。

4 磁流变减振器实验结果分析

依据试验条件，利用科马智能悬架技术(青岛)有限公司试验中心的PWS-16电液伺服减振器综合性能试验台进行试验。试验前先将自制的磁流变减振器拉伸至极限位置后封闭，然后将其垂直安装在试验台上，预压缩约1/2的工作行程，并以此为试验起始点，保证压缩行程终止时活塞总成不会进入缓冲区段。设定输入正弦激励振幅为±40 mm；正弦最高激振速度分别为0.050、0.131、0.262、0.393、0.524、0.750、1.000 m/s；输入激励电流分别为0、0.5、1.0、1.5、2.0、2.5、3.0、2.5-、2-、1.5-、1-、0.5-、0-A等，其中“-”表示电流下降阶段。一般操作试验台对被测试的磁流变减振器进行5～8次往复运动并进行采样，确定减振器的压缩、复原阻尼力值，从而生成一个完整周期的示功曲线。

4.1 磁流变减振器示功特性

按照设定的试验条件进行试验后，导出不同励磁电流下磁流变减振器的示功特性数据，仅绘制标记06号磁流变减振器示功特性曲线，阻尼力-位移(F-S)曲线如图8所示。

4.2 磁流变减振器速度特性

同样，按照设定的试验条件进行试验后，导出不同励磁电流下磁流变减振器的速度特性数据，由于篇幅原因仅绘制标记02号和标记06号优化前、后磁流变减振器的速度特性曲线，阻尼力-速度(F-V)曲线如图9、图10所示。

对应的，只详细列举标记02号和06号优化前、后磁流变减振器加载最小电流0 A和最大电流3 A情况下输出的阻尼力值，详细力值信息如表5、表6所示。

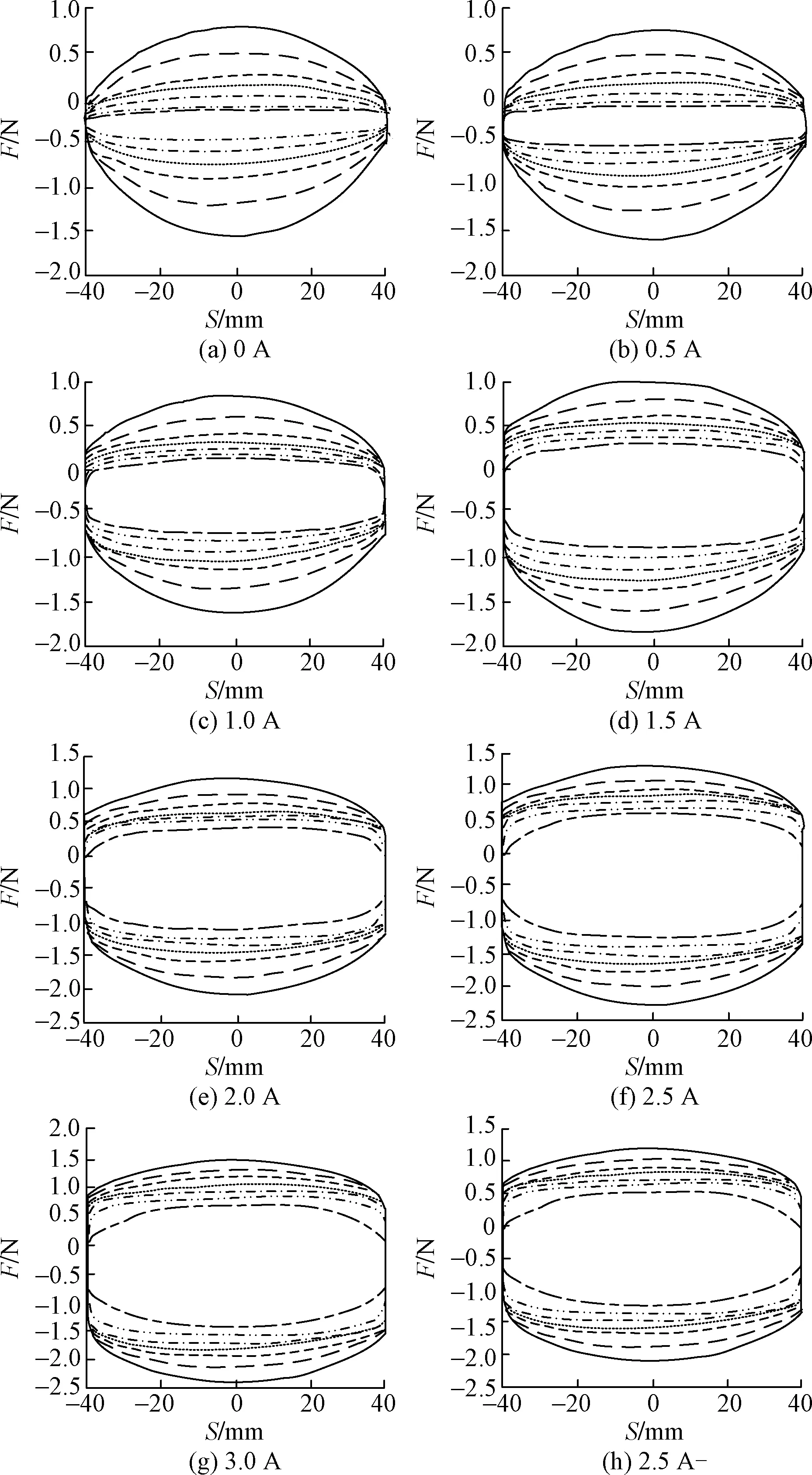
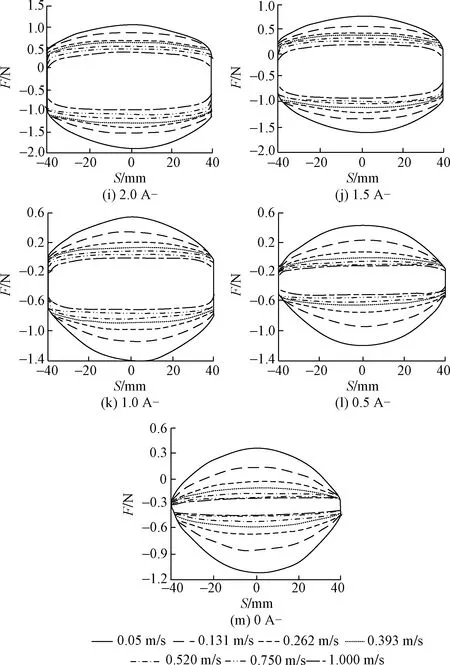
图8 06号磁流变减振器在不同电流下的F-S曲线Fig.8 The F-S curve of the No. 06 MRD at different currents

图9 02号磁流变减振器在不同电流下的F-V曲线Fig.9 The F-V curve of the No.02 MRD at different currents

图10 06号磁流变减振器在不同电流下的F-V曲线Fig.10 The F-V curve of the No.06 MRD at different currents

表5 02号磁流变减振器加载0 A和3 A电流情况下 的阻尼力值Table 5 The damping force values of No.02 MRD under load of 0 A and 3 A currents

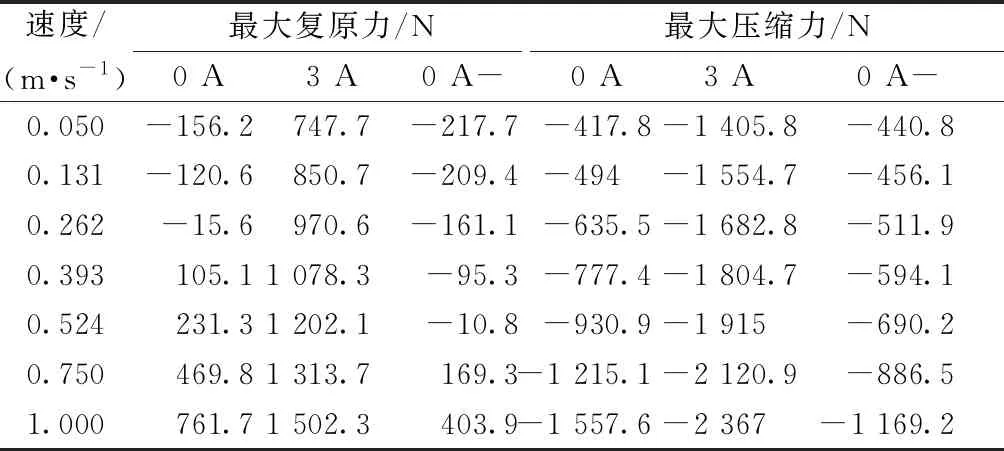
表6 06号磁流变减振器加载0 A和3 A电流情况下 的阻尼力值Table 6 The damping force values of No.06 MRD under load of 0 A and 3 A currents

4.3 试验结果分析

通过分析F-S与F-V磁流变减振器特性图，可以得到以下结论。

(1)从图8所示的磁流变减振器F-S特性曲线图可以看出，在其他加载条件不变的情况下(相同激振频率)，仅加大激励电流，随着电流强度的增大，减振器活塞总成中的线圈产生的磁场不断加大，因而磁流变液处的磁感应强度不断增加，促使磁流变液的屈服强度变大，进而磁流变减振器输出的阻尼力不断加大，说明磁流变减振器阻尼的可控性以及输出阻尼力与电流之间存在一定的函数关系。

(2)从磁流变减振器F-V特性曲线图可以看出，自制的磁流变减振器在设定行程为(80±40)mm运动时，其输出的阻尼力随着电流与速度的增大而增大。在速度为零的区域附近即在低速区时，磁流变减振器输出阻尼力产生较明显的迟滞环现象，这与磁流变液在屈服前的黏-弹性现象有关；而且磁流变减振器在低速运动时，由于其工作缸内的磁流变液存在剪切稀化的现象，会导致磁流变减振器屈服前区等效黏度慢慢变小而持续到其屈服后的黏度；而在高速运动时则几乎呈线性关系。这与减振器本身的弹性以及磁流变液的黏-弹-塑性有关。

(3)同一电流情况下，随着速度的增大，示功曲线包络的面积与磁流变减振器每个振动周期消耗的能力成正比，即反映出示功曲线包络的面积越大，磁流变减振器的减振性能越好。

(4)自制磁流变减振器采用浮动活塞气体补偿结构，由于充气反拨力的存在，使得示功图向下方偏移。

(5)前后两次0 A时，阻尼力出现了较大变化，这与温度、摩擦力等因素有关。在第一次电流为0 A时，此时减振器内的磁流变液由于沉降的缘故，不是混合均匀的，当电流再次降为0 A，磁流变液完全混合均匀，造成阻尼力减小；同时温度的变化也会引起阻尼力的变化。

(6)通过对比表5和表6优化前、后磁流变减振器在不加载电流0 A和加载最大电流3 A情况下，对应不同速度条件下输出的阻尼力值，发现结构优化后的磁流变减振器输出的阻尼力较优化前的大。其中，在0 A、速度最大时，复原力提高了15.7%，压缩力提高了36.8%；在3 A、速度最大时，复原力提高了3.5%，压缩力提高了21.5%。通过对试验结果的分析可知，设计的结构参数符合磁流变减振器实际应用需求。

5 结论

通过搭建磁流变减振器多目标优化模型进行结构优化设计并通过试验验证优化解的可靠性，可以得出以下结论。

(1)利用modeFRONTIER多目标优化软件，基于Pareto集和Bingham模型进行磁流变减振器结构参数优化具有一定的可靠性，大大提高磁流变减振器设计开发时间，节约研发成本，具有一定的工程应用价值。

(2)采用Bingham模型进行优化设计的磁流变减振器最大阻尼力与最大动力可调系数值呈负相关关系，其中阻尼通道间隙对两优化目标影响最大。

(3)对于磁流变减振器阻尼力而言，在一定约束条件下，活塞的有效长度存在最优值。

(4)通过试验得出结构优化后的磁流变减振器输出的阻尼力较优化前的大,验证了本文优化设计的单筒式磁流变减振器的可靠性，对今后磁流变减振器的设计具有一定的参考价值。