改进的黏弹材料应力松弛模型
康永刚, 张秀娥
(防灾科技学院, 三河 065201)
在取定应变的情况下,应力随时间增加而减小的现象,称为应力松弛。应力松弛对评价黏弹材料的长期使用很重要,相应的理论和方程是材料科学的重要研究内容[1]。常见的黏弹性模型由虎克弹簧和牛顿黏壶组合得到,由它们的本构方程可以得到相应的应力松弛函数[2]。近几十年,分数模型的研究是热点[3-4],它们的本构方程含有分数阶导数或积分,相应的应力松弛函数含有Mittag-Leffler函数。工程上,经验松弛公式[5-6]也比较常用。在实际应用时,这些模型都有一定的局限性[7]。由弹簧和黏壶构造的模型,优点是形象直观、物理意义明确。缺点是要准确描述实验数据,需要含较多弹簧和黏壶的结构,即包含较多的待定参数,从而计算难度也会增加。用相对较少的参数给出实验数据比较精确的描述,是构造模型时必须考虑的问题。
一些研究者指出,可结晶性聚合物表现出两种典型的应力松弛行为:当初始应力较大或温度较低时,松弛速率与应力满足指数关系(exponential law);当初始应力较小或温度较高时,松弛速率与应力满足幂律关系(power law)[8]。许多研究者从松弛动力学角度来研究该现象。唯象黏弹模型与实际工程应用紧密相连,但是各种模型并没有给出松弛速率与应力的这种关系。
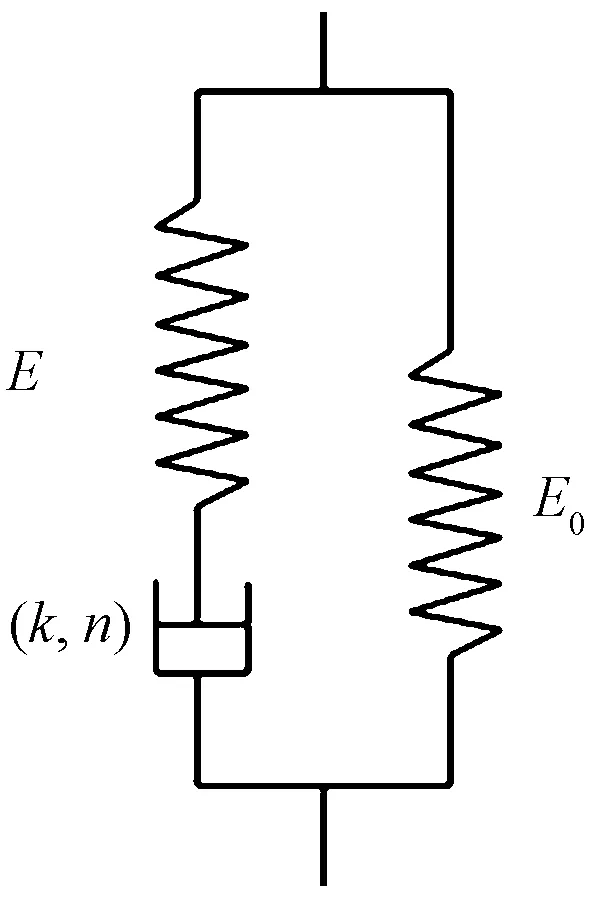
经典黏弹模型中的黏性元件为牛顿黏壶。实际流体不一定符合牛顿流动定律,如黏度不是常量,具有屈服应力、弹性特性、触变流体等[9]。用假塑性黏壶与弹簧串联,得到改进的Maxwell模型。改进的Maxwell模型再与弹簧并联,给出改进的Zener模型。并且得出松弛速率与应力满足幂律的关系及幂律型松弛函数。
1 改进的Maxwell模型
牛顿流体满足条件为

(1)
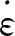
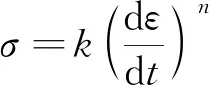
(2)
式(2)中:k和n为材料参数。
满足式(2)的黏壶,有假塑性黏壶(0
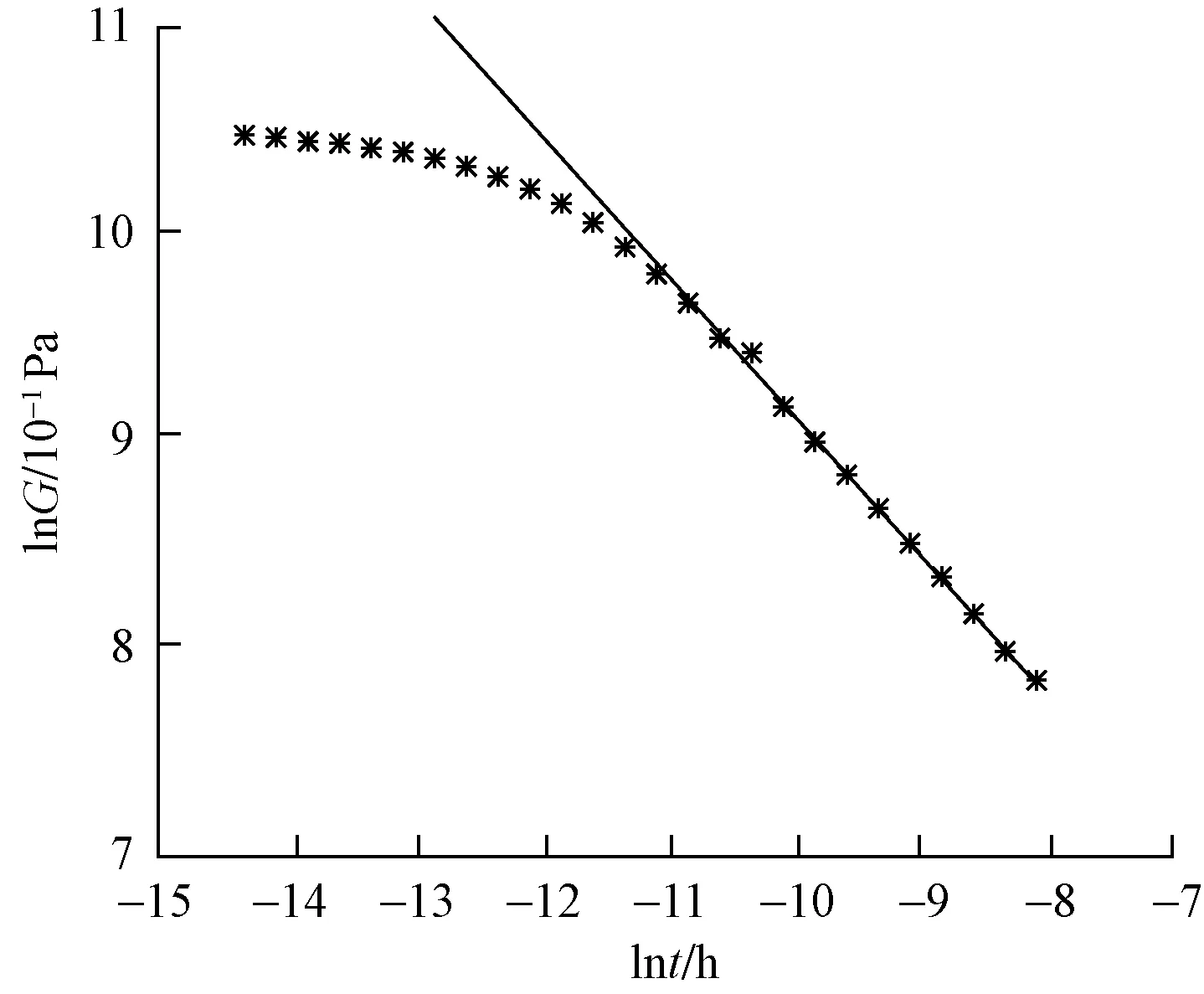
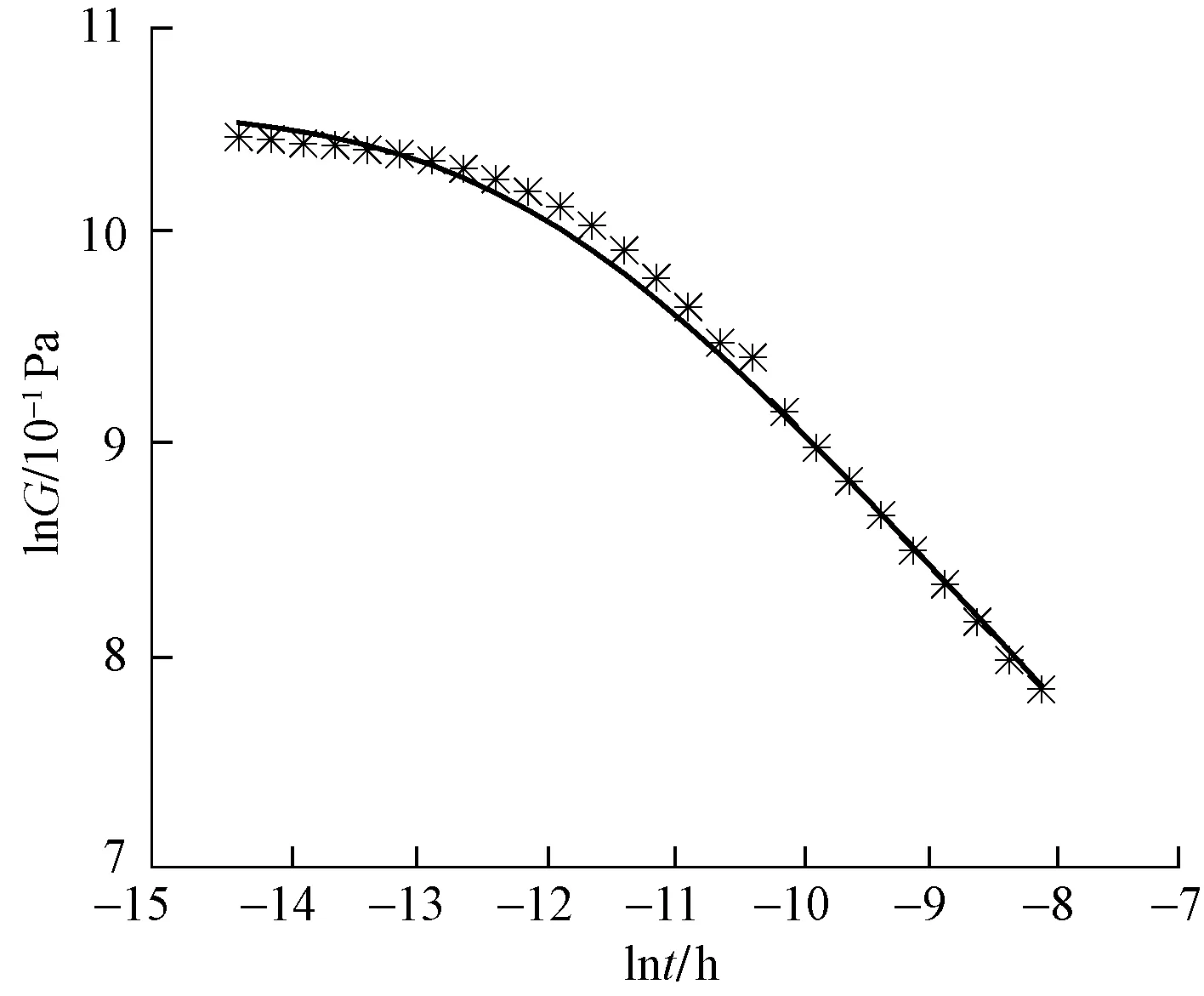
Maxwell模型是虎克弹簧和牛顿黏壶的串联结构,能定性描述应力松弛过程,不能描述材料的实际蠕变行为。用满足式(2)的假塑性黏壶(即0 (3) 由式(2)得 (4) 式(3)和式(4)相加,给出改进的Maxwell模型的本构方程为 (5) 图1 改进的Maxwell模型Fig.1 Modified Maxwell model 蠕变时应力为定值,该模型的蠕变函数(时间的一次函数)与实际材料蠕变行为并不相符。 应力松弛时应变为常数ε0,可得到松弛方程为 (6) 式(6)中:K为常数。 松弛速率与应力之间存在幂律关系。 式(6)作为一种非Debye松弛方程,引起一些研究者的兴趣[12]。应变取定值ε0,对式(5)分离变量求定积分,由于初始时刻σ0=Eε0,得到式(5)对应的松弛函数为 (7) 或整理为相对简洁的形式为 σ=(t/τ+c)-α (8) σ=(t/τ)-α (9) 可见,常见的幂律型松弛为式(7)的近似情况,可把式(7)称为改进的幂律型松弛。许多材料的松弛曲线满足幂律函数式(9),但一般只是当作一种经验公式来用。利用假塑性黏壶构建改进的Maxwell模型,给出该类松弛的本构方程,以及幂律函数的指数α与表示材料非线性的参数n的关系。图2是指数α随参数n的变化曲线,α随n的增大而变大。式(9)有一个不足,即初始时刻时趋于无穷大,与实际情况不相符。改进的Maxwell模型的松弛方程式(7)克服了这一局限。 图2 α随n的变化曲线Fig.2 The curve ofα following n 下面推导式(7)与Debye型松弛的关系。式(7)可变为 (10) 进一步对指数进行改写,得到 (11) σ=Eε0e-Et/k (12) 注意,此时k=η。即经典的Maxwell模型作为一种特例,包含在改进的Maxwell模型中,即Debye型松弛是幂律型松弛式(7)的特例。 图3(a)是n取值变化时,式(7)在双对数坐标下改进的Maxwell模型的松弛曲线,其他参数分别为E=100 Pa,k=0.05 Pa·sn和ε0=0.1。注意,由式(2)可知,参数k的单位与指数n有关。可见,松弛曲线可分为两个区域。而比较常用的经验松弛函数f(t)=(t/τ)-α在此类坐标下为直线,对表现为两个区域的松弛过程是不能描述的。图3(b)是k取不同值时,式(7)在双对数坐标下的曲线,其他参数分别为n=0.9,E=100 Pa和ε0=0.1。时间增加,k值对曲线的影响越大。图3(c)是E取不同值时,式(7)在双对数坐标下的曲线,其他参数分别为n=0.9,k=0.05 Pa·s0.9和ε0=0.1。可见,E对整个时间域的松弛曲线都有明显影响。 图3 幂律松弛函数式(7)的松弛曲线Fig.3 Power function Eq.(7) Zener模型(标准固体模型)既可以定性描述黏弹性材料的应力松弛特征,也可以定性描述其蠕变特征。Zener 模型是一种三元件模型,由一个Maxwell 单元和一个虎克弹簧并联得到。用改进的Maxwell模型与弹簧并联,得到一种改进的Zener模型(图4)。并联时应变相同,这两部分分别满足方程式(13)和式(14),即 (13) σR=E0ε (14) 式中:σL为左边改进的Maxwell单元的应力;σR为右边弹簧的应力。 式(14)两边同乘以E-1k1/n,加到式(13)两边,得到 (15) 式(15)变为 (16) 式(14)两边加到式(16)两边,得到改进模型的本构方程为 (17) 并联时合应力为各部分应力之和,改进的Zener模型松弛函数为改进的Maxwell单元和弹簧E0的松弛函数之和,即 σ=[α-1Ek-1/nt+(Eε0)-1/α]-α+E0ε0 (18) 式(18)中:α=n/(1-n)。当t较大时,忽略求和项(Eε0)-1/α,式(18)可简化为σ=At-α+B形式,该松弛函数也比较常用。σ0表示常应力,此时对式(17)进行分离变量求定积分,由于t=0时σ0=ε0(E0+E),所以改进的Zener模型的蠕变函数为 (19) σ=Eε0e-Et/k+E0ε0 (20) (21) 因此,经典模型可认为是改进模型的一种特殊情况。 图5是E0分别为1、2、3 Pa时式(18)的松弛曲线,其他参数分别为n=0.9,k=0.05 Pa·s0.9,E=100 Pa,ε0=0.1。可见,改进的Zener模型松弛曲线可分为三个区域,E0主要影响第三个区域。 图4 改进的Zener模型Fig.4 Improved Zener model n=0.9, k=0.05 Pa·s0.9, E=100 Pa,ε0=0.1图5 松弛函数式(18)的松弛曲线Fig.5 Stress relaxation function Eq.(18) 图6 式(9)对聚异丁烯应力松弛模量的拟合Fig.6 Eq.(9) fit of stress-relaxation modulus of polyisobutylene 图7 式(8)对聚异丁烯应力松弛模量的拟合Fig.7 Eq.(8) fit of stress-relaxation modulus of polyisobutylene (1)用假塑性黏壶与弹簧串联,得到改进的Maxwell模型。改进的Maxwell模型再与弹簧并联,得到改进的Zener模型。常应变时,可得出松弛速率与应力满足幂律关系。 (2)求解本构方程得到改进的幂律型松弛函数。常见的松弛函数f(t)=(t/τ)-α是改进松弛函数的一种近似情况,而Debye型松弛是改进松弛函数的极限情况。并且改进松弛函数,克服了函数f(t)=(t/τ)-α当t→0时趋于无穷大的缺点。 (3)在双对数坐标中,松弛函数f(t)=(t/τ)-α为直线,而改进的幂律型松弛函数分为两个区域,其中一个区域近似为直线。因此,改进的幂律型松弛函数对于一部分为直线的松弛过程比较适用。并且拟合比较方便,可先拟合直线确定部分参数。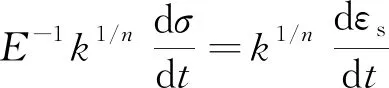

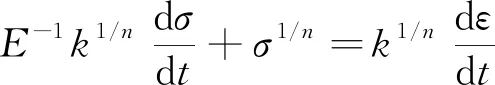

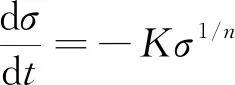
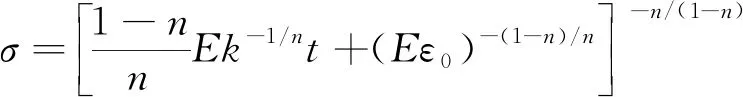


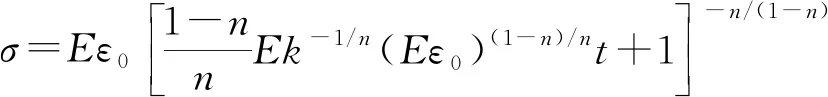
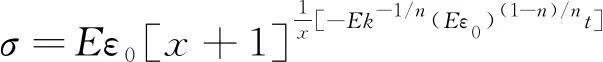
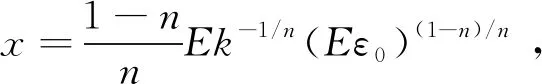

2 改进的Zener模型
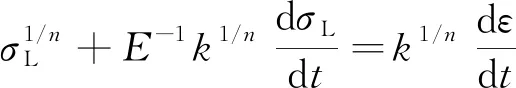
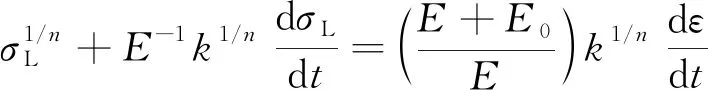

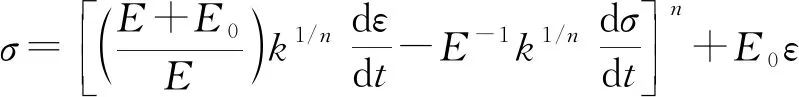
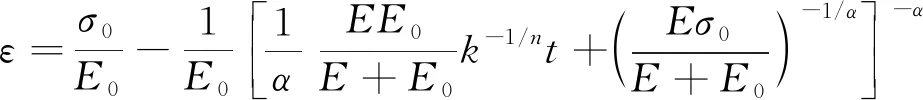
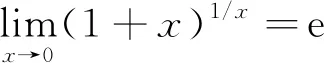
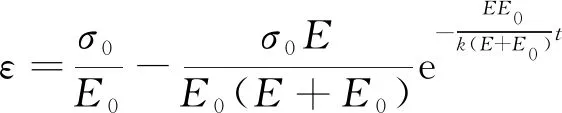
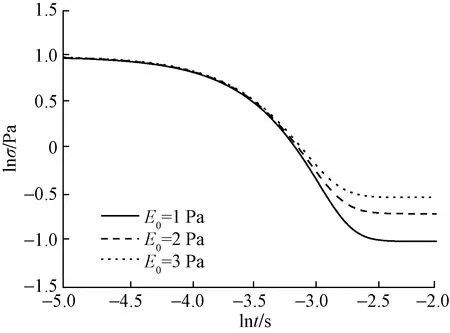
3 对聚异丁烯松弛模量的研究
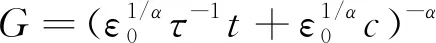
4 结论

