顾及强电离层活动的三频周跳探测与修复算法

崔立鲁, 许文超, 邹正波, 杜 安, 李 盼, 安家春

(1.成都大学建筑与土木工程学院， 成都 610106； 2.武汉大学测绘学院， 武汉 430079； 3.中国地震局地震研究所， 中国地震局地震大地测量重点实验室， 武汉 430071； 4.武汉大学中国南极测绘研究中心， 武汉 430079)

高质量的载波相位观测数据是实现高精度导航定位服务的必要条件，而载波相位观测数据因易受电离层活动影响，从而导致周跳的发生[1]。虽然目前周跳探测与修复的算法很多，如：伪距相位组合法[2-3]、无几何组合法[4-5]、TurboEdit法[6]、MW(Melbourne-Wbbena)组合[7]等，但是忽略了电离层延迟的影响。针对强电离层活动下的周跳探测问题，中外学者对此进行了大量的研究。文献[8]利用三个线性无关的三频无几何无电离层组合构成周跳探测检验量以解决强电离层风暴下的周跳探测问题，但是由于引入了伪距观测量，该方法受伪距噪声影响较大，不利于小周跳的探测；文献[9]采用三频无几何消电离层组合联合MW组合和电离层残差组合对电离层变化剧烈情况下的周跳进行探测与修复，但文中针对的是双频观测值，并没有对三频观测进行讨论；文献[10]提出联合三个线性无关组合对强电离层活动下的周跳进行探测，并利用最小二乘模糊度降(least-square ambiguity decorrelation adjustment， LAMBDA)算法对周跳整数解进行搜索并确定。

针对强电离层活动下三频周跳探测问题，构建了由1个无几何无电离层(geometry-free and ionosphere-free，GIF)码相组合和2个无几何相位二阶差分(second-order time-difference geometry-free phase, STGFP)组合组成的周跳检验量，根据电离层延迟和组合观测值噪声最小原则筛选出最优组合系数，并利用空间搜索法和1范数最小原则对周跳值进行正确修复，最后利用全球导航卫星系统(global navigation satellite system，GNSS)三频实测数据对本算法进行验证，并得到相应的结果。

1 三频组合观测值的构建

1.1 三频无几何无电离层码相组合

根据三频信号特点，为了能够消除与几何相关误差和电离层延迟一阶项的影响，构建了三频GIF码相组合[10]，其表达式为

Nαβγ=αN1+βN2+γN3=

(1)

式(1)中：α,β,γ∈Z为载波相位组合系数；l,m,n∈R为伪距组合系数；Nαβγ和λαβγ为组合整周模糊度和波长；φi,Pi,Ni(i=1,2,3)分别为GNSS三个频点的载波相位观测值、伪距观测值和整周模糊度。对式(1)历元间求差，可得其周跳探测方程为

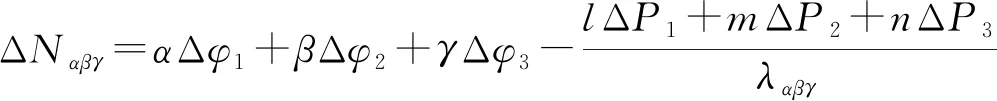
(2)

假设GNSS三个频率的伪距和载波相位观测噪声均相同，式(2)中ΔNαβγ的标准差为

(3)

式(3)中：σφ和σP分别为载波相位和伪距观测噪声的标准差，其值分别为0.01周和0.3 m[5]。以fσΔNαβγ为周跳探测阈值，当ΔNαβγ值大于探测阈值时，则认为发生了周跳。

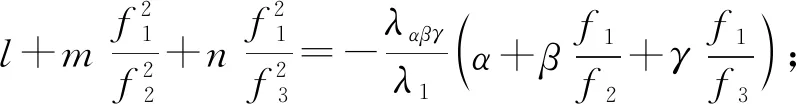
表1 GPS三频GIF码相组合Table 1 GPS triple-frequency GIF code-phase combination

表2 BDS三频GIF码相组合Table 2 BDS triple-frequency GIF code-phase combination

由表1和表2可知，探测阈值并不是组合波长越长越小，而是由载波和伪距组合系数综合确定的。当探测阈值设为3σΔNαβγ时，表1和表2中前5行和前6行的组合系数均能探测出包含1周以内的所有周跳。而当探测阈值变为4σΔNαβγ时，只有GPS系统的(0,1,-1)和BDS系统的(0,-1,1)组合满足上述要求(表1、表2中的加粗字体数据)，因此将探测阈值设为3σΔNαβγ。由于本组合的无几何特性，存在着类似于ΔN1=ΔN2=ΔN3的不敏感周跳，所以构建三频周跳检验量只依靠GIF码相组合是不行的，必须引入其他组合。

1.2 三频STGFP组合

三频无几何(geometry-free，GF)相位组合的表达式[5]为

aλ1φ1+bλ2φ2+cλ3φ3=-ηabcI+aλ1N1+bλ2N2+cλ3N3

(4)

式(4)中：(a,b,c)∈Z为载波组合系数，且满足a+b+c=0；I为电离层延迟。对式(4)进行历元间求差，可得

ΔNabc=aλ1ΔN1+bλ2ΔN2+cλ3ΔN3=

aλ1Δφ1+bλ2Δφ2+cλ3Δφ3+ηabcΔI

(5)

由式(5)可知，GF相位组合周跳探测方程中含有电离层延迟一阶项ηabcΔI。在一般情况下，ηabcΔI很小，可以忽略不计。但是当电离层处于活跃期时，ηabcΔI的数值会发生剧烈的波动，这会造成周跳探测结果的不准确[12]。因此必须考虑电离层延迟的影响，采用文献[8]中对三频GF相位组合进行历元间求差以削弱强电离层活动影响。因此，STGFP组合周跳探测方程可表示为

aλ1Δφ1+bλ2Δφ2+cλ3Δφ3-ηabcΔI

(6)

(7)

由式(7)可知，三频STGFP组合主要受载波观测噪声影响，因此其探测阈值较小，探测精度较高，采用4σ作为探测阈值。为了提高周跳探测精度，筛选组合系数时以ηabc最小和σ最小为原则，部分结果如表3和表4所示。

由表3和表4可知，三频STGFP组合的4σ均小于三频GIF码相组合的4σΔNαβγ，说明三频STGFP组合的周跳探测能力要优于三频GIF码相组合。表3、表4中第4列“探测变化量”是指由特殊周跳(1,1,1)引起的周跳探测量变化，第5列的N为探测阈值相对于探测变化量的倍数。虽然某些组合系数受电离层延迟因子影响较小，但是其探测变化量远小于周跳探测阈值，这就意味着无法探测到类似(1,1,1)的不敏感周跳，如表3中(2,-11,9)所示，其ηabc为0.004 385，为表中最小值，其探测阈值为1.136 836周，探测变化量为-0.012 273，N为-23，为最大值。因此为了保证对特殊周跳的探测能力，必须使N尽可能地小。因此，选择N=0的组合系数作为最优组合，表3、表4中的加粗字体数据分别为根据上述分析选取的GPS和BDS组合系数及其相关参数。

表3 GPS三频STGFP组合Table 3 GPS triple-frequency STGFP combination

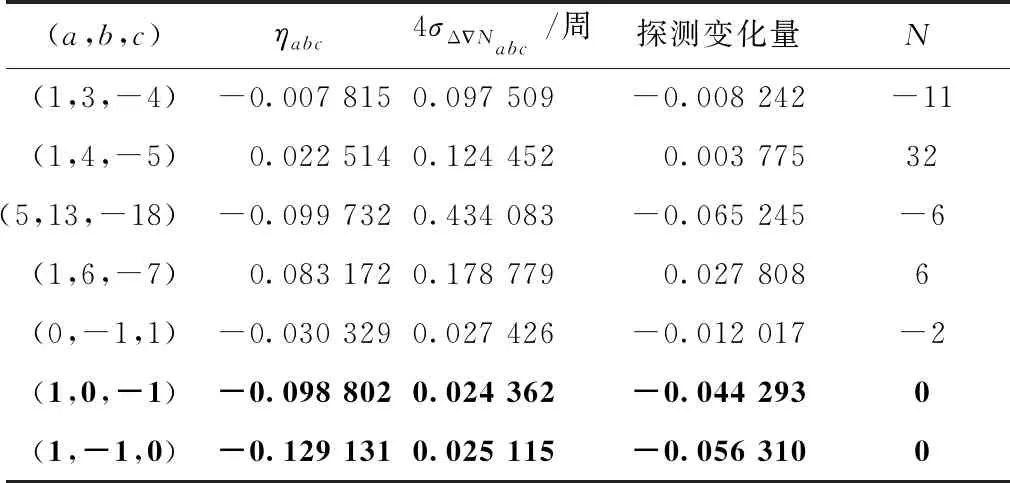
表4 BDS三频STGFP组合Table 4 BDS triple-frequency STGFP combination

2 周跳的修复

利用GIF码相组合和STGFP组合实现三频周跳的修复必须构建三个周跳探测方程，这就需要三个线性无关的组合系数[13-16]。由1.1节和1.2节的分析可知，虽然GIF码相组合能够更有效地消除电离层延迟对周跳探测与修复的影响，但由于引入了伪距观测噪声，其探测阈值较大，在探测阈值为4σΔNαβγ的情况下能够探测包括1周以内所有周跳的组合系数只有1组；而STGFP组合因为只含有载波观测值，其探测阈值较小，有利于对小周跳的探测，同时满足要求的组合系数不止一个。因此采用1个GIF码相组合和2个STGFP组合构建周跳检验量，其周跳修复表达式[17-20]为

(8)

式(8)中：(α,β,γ)为三频GIF码相组合中的载波组合系数，(a1,b1,c1)和(a2,b2,c2)为两个STGFP组合系数；ΔNi(i=1,2,3)分别为GNSS三个频点的周跳值；ΔNαβγ为三频GIF码相组合的周跳检验量；ΔNa1b1c1和ΔNa2b2c2分别为2个三频STGFP组合的周跳检验量。

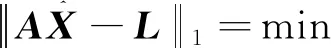
(9)

3 实验分析

为了充分验证本文算法在强电离层活动下的周跳探测与修复能力，采用cut0站点的三频GNSS实测数据，时间段为2013年3月17日0:00—24:00，采样间隔为30 s，高度截止角为10°，接收机型号为Trimble NetR9，天线型号为TRM59800.00。文献[16]表明，在上述时间段该站点上空发生了强烈的电离层风暴，电离层延迟变化出现了剧烈的变化。选取上述GNSS三频实测数据中GPS G25和BDS C08两颗卫星的观测数据进行实验。

根据第1节和第2节的分析，选取GPS系统的三频GIF码相组合(0,1,-1)和STGFP组合(1,-1,0)、(1,0,-1)，BDS系统的三频GIF码相组合(0,-1,1)和STGFP组合(1,-1,0)、(1,0,-1)进行周跳探测与修复实验。为了验证强电离层活动对周跳检验量的影响，上述组合系数的历元间一次差分值和二次差分值计算结果如图1所示。

如图1(a)和图1(b)所示，GPS三频GIF组合(0,1,-1)和BDS三频GIF组合(0,-1,1)因其本身具有无电离层性质，因此对强电离层活动影响具有一定的削弱作用，但是由于引入了伪距噪声，其探测阈值远大于三频STGFP组合。根据图1(c)、图1(e)、图1(g)和图1(i)可知，在强电离层活动的情况下，三频GF相位组合(即历元间一次差分)的周跳检验量出现了较大的波动，从701历元处开始，GPS系统受到电离层活动影响的部分远远超过了探测阈值的范围(图中红色虚线)；而BDS系统受到的影响要小于GPS，其周跳检验量的波动要小于GPS系统，但是也存在不稳定的情况(位于1 001历元左右)，且有部分检验量超过了阈值范围。对上述三频GIF相位组合进行历元间二次差分后(即STGFP组合)，其周跳检验量大幅减少，无论是GPS系统还是BDS系统的周跳检验量均在探测阈值以内，并且在0附近上下浮动，基本上消除了强电离层活动对周跳探测的影响。因此采用1个三频GIF相位组合和2个三频STGFP组合所构成的周跳检验量能够有效地削弱强电离层活动对周跳探测的影响。

为了进一步验证本文算法的周跳探测性能，分别在G25和C08两颗卫星的三频实测无周跳无粗差载波相位观测值的观测历元中每隔10 s加入(0,0,1)到(2,2,2)共计26个随机小周跳，具体计算结果如图2所示。

由图2可知，无论GPS系统还是BDS系统，本文算法均能实现对所有小周跳的探测。由于小周跳的探测难度要远大于大周跳，因此可以认为本文算法能够有效探测所有大小的周跳。在利用式(8)修复周跳时采用直接取整法，但是得到的结果并不完全正确，如表5所示。表5中加粗部分为采用直接取整法修复失败的周跳。原因主要是因为STGFP组合受到电离层延迟残差和观测噪声的影响[13]。由表5可知，出现修复失败的次数较多的是GPS系统，这从侧面说明GPS系统的观测噪声要略大于BDS系统，这与文献[13]中得到的结果一致。

为了避免这个现象的出现，采取空间搜索法和1范数最小原则对表5中修复不正确的结果进行重新计算、确认，计算结果如表6所示。由表6可知，GPS和BDS系统均存在着1范数最小值对应的周跳修复值不正确，而第二最小值却是正确的现象(表6中加粗字体的数据)，其中GPS系统出现2次，BDS系统出现1次。这是由于GF相位组合(1,-1,0)受到观测噪声影响，导致1范数最小所对应的周跳检验量无限地接近于探测阈值，导致了误判的出现。为了避免这样的问题，必须对周跳修复结果进行确认，即对修复后的观测值重新进行周跳探测。

图1 GNSS三频周跳检验量Fig.1 GNSS triple-frequency cycle-slip detection value

4 结论

鉴于强电离层风暴对周跳探测结果的影响，采用三频GIF伪距相位组合和三频GF相位组合构建三频周跳检验量实现对GNSS三频周跳探测与修复，并利用GNSS三频实测数据对本文算法进行验证。验证结果表明：本文算法可以有效解决在强电离层活动情况下周跳探测与修复问题。在对周跳进行修复的过程，针对电离层延迟和观测噪声对修复结果的影响，采用空间搜索法结合1范数最小原则实现周跳的精确修复，但是受观测噪声的影响，由1范数最小得到的周跳修复值可能存在着错误，必须采用再次周跳探测的方法对周跳修复结果进行确认。综上所述，本文算法适用于强电离层活动情况下的周跳探测与修复，可以用于高精度的导航定位服务。

图2 小周跳探测Fig.2 The small cycle-slip detection