基于Burgers模型铁路路基长期沉降的预测分析

王 威，杨文豪，杨成忠，冯青松

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013)

铁路路基是承受并传递轨道重力及列车动力作用的结构基础，是铁路构造之中不可或缺的重要组成部分，尤其是其稳定性对于保证列车安全高速运行起着至关重要的作用[1-3]。而铁路路基的长期沉降变形又是影响列车行车安全性、行车速度、乘客舒适度和路基稳定性的关键因素，其产生的原因主要是与路基填料堆载、列车循环荷载作用和路基土的蠕变特性等有关。为保证行车的安全性和乘客的舒适度，如何准确有效地计算与预测路基沉降变形已成为关键问题[4-5]。近年来，国内外学者围绕这一课题展开了较多的研究，根据目前所采用预测路基沉降的计算方法大致可分为三类：

第一类为建立在弹性半无限体假定基础上经典的分层总和法，其利用简化的固结公式计算固结度，然后推算沉降发展规律。吕玺琳等[6]对软土空心柱在交通荷载应力下的扭剪试验数据进行分析，结合分层总和法、累积孔压经验公式和软黏土累积塑性变形规律，建立了软土路基长期沉降拟静力计算模型。周同和等[7]通过分析二元复合地基的受力特点，提出了复合模量分层总和法计算路基沉降。虽然上述方法能计算并预测路基沉降，但计算出的结果往往与实测沉降有较大差异[8]。

第二类为数值计算法，其根据固结理论并结合土体的本构关系模型，计算最终沉降量及其发展规律。郭超等[9]以京津城际轨道交通天津段路基工程为依托，采用剑桥模型来模拟土体的力学行为，并结合现场原位测试数据，对路基土的长期沉降变形进行预测。但数值计算法的参数难以确定，同时由于路基工程的复杂性，难以考虑所有因素[10]，故该法不易为工程人员快速掌握。

第三类为根据现场实测数据推算沉降量与时间的关系，归纳起来主要有曲线拟合法、灰色理系统法、人工神经网络法和反分析法。其中曲线拟合法包括双曲线法[11]、指数曲线法[12]、星野法[13]、Asaoka法[14]、泊松曲线法[15]等，从计算方法上来说，曲线拟合法是一种较为完善的方法且简单实用，但其前期沉降预测稳定性较低，与实际值有微小偏差[16]。灰色系统模型虽具有较强的适应性，但拟合出的模型参数较实际参数偏小[17]。人工神经网络具有很强的非线性映射能力，但存在拟合过程受局部极小点的困扰。反分析法是目前工程中校准物理力学参数常用的方法，但反演过程较为繁琐[18]。

事实上，铁路路基工程具有其自身的特殊性和复杂性，路基填料的类型、堆积高度以及列车的循环荷载和土的蠕变特性等都会影响路基的长期沉降。而上述计算预测路基沉降的方法多是单一的考虑路基土在填料堆载或列车循环荷载作用下的变形特性，同时也未考虑土的蠕变特性及其所处应力环境，可能会导致模型的预测结果有所偏离。因此，本文基于Burgers模型，在充分考虑铁路填筑及列车运营期间路基土所处的空间应力状态及蠕变特性的基础上，通过分析铁路路基中任意单元体沉降量来预测路基长期沉降变形量，并利用路基实际的沉降数据验证模型的合理性，成果可为今后在类似实际工程应用中提供一定的借鉴。

1 铁路路基沉降预测模型

铁路路基的长期沉降变形一般从前期的填筑开始直至后期的铁路运营始终在不断发展。在前期的填筑过程中，路基土主要承受填料的静载作用，该阶段路基的沉降变形主要是由路基土自身的蠕变特性和各结构层填料的堆载压实所造成的；而在后期的铁路运营中，路基会承受列车的荷载作用，此时路基的沉降变形主要与列车的循环荷载、填料堆载大小、时长以及路基土的蠕变特性等因素有关。目前，在路基的长期沉降预测的模型中，Burgers模型[19]具有应力-应变关系式简单、参数概念明确、应用较为方便且精确度较高等优点。因此，基于Burgers模型，充分考虑路基土在填料堆载及列车荷载作用下的空间应力状态以及蠕变特性，对路基中任意单元体的沉降变形特性进行研究，进而预测铁路路基长期沉降变形量。任意土体单元在路基填料堆载或列车荷载作用下所处的空间应力状态示意见图1。

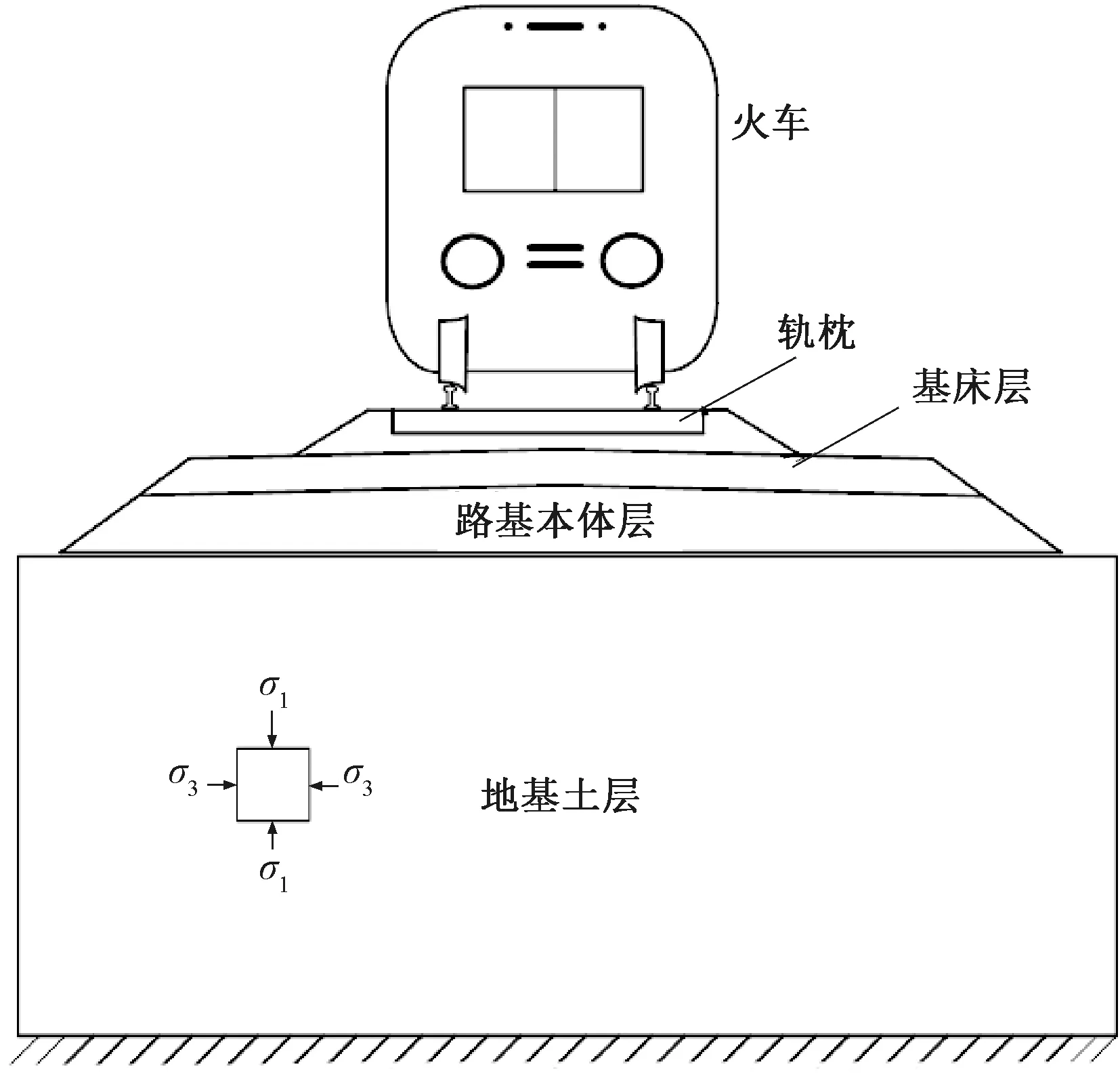
图1 任意土体单元的受力情况

Burgers力学模型见图2，是由Maxwell模型和Kelvin模型串联而成[20-21]。由于Burgers模型的本构方程较为复杂，若直接从其本构方程中求解出其方程的过程及微分方程都非常的繁琐。故本文采用分解组合模型元件的方法，即分别从Maxwell模型和Kelvin模型的本构模型出发，推导出这两个模型的沉降变形方程后再进行叠加，最终得到基于Burgers模型预测铁路路基长期沉降变形方程。

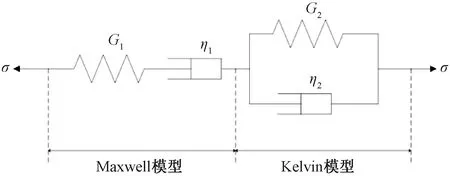
图2 Burgers模型示意

1.1 路基填筑及列车荷载表达式的选取

事实上，铁路在修建期间，路基土主要承受填筑材料的静载作用，而后在运营期又会承受来自列车的动荷载作用，因此对于任意深度z的路基土体来说，可能会受到填料堆载、轨道结构自重和列车荷载等作用力的影响，可表示为

Fz=FT+FD

(1)

式中：FT为路基填料堆载及轨道自重所产生的作用力，为了计算简便，本文对轨道结构自重做了简化，将其等效为某一填料的堆载作用[22]；FD为列车荷载所产生的作用力；Fz为距路基上表面z处路基土所承受总的作用力，在运营期间，若无列车荷载，则总作用力等于FT。

而列车在运行中对路基土所产生的力主要是通过其轮轨之间的作用力所形成的，故轮轨力的作用大小及时间会直接影响到路基内部土体的沉降变形程度。影响轮轨力的主要因素包括轨道不平顺和轨面波形磨耗效应，加之铁路线路运营环境复杂多变，致使轨道不平顺具有相当的随机性[23]。为此，各国开展了大量理论和试验研究，并总结出多类维修管理标准，如英国轨道几何不平顺管理标准见表1。

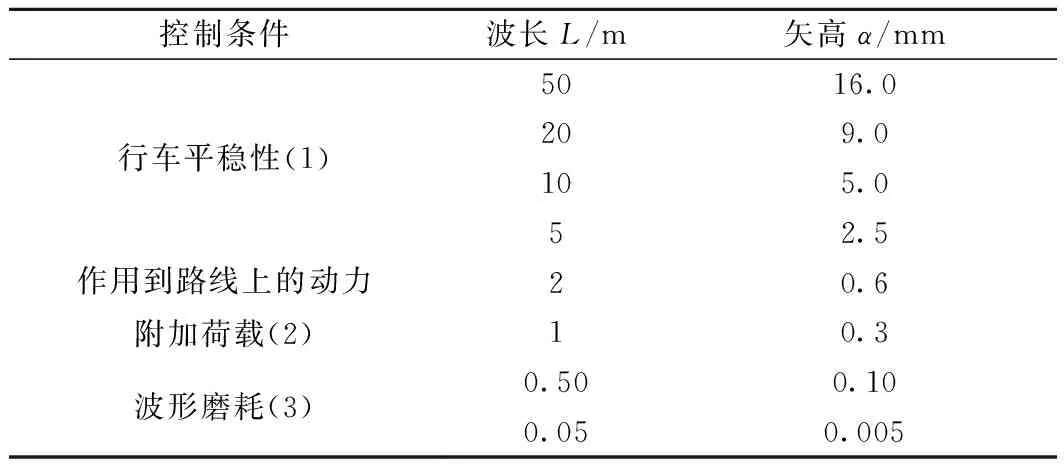
表1 轨道几何不平顺值

为有效计算列车荷载，并综合考虑车速、轨道几何不平顺等因素的影响，本文选用文献[23]提出的可反映轨道不平顺、附加动载和轨面波磨效应的激振力函数来模拟列车荷载，其表达式为

FD=F(t)=P0+P1sinω1t+P2sinω2t+P3sinω3t

(2)

式中：P0为车轮静载；t为时间；Pi、ωi分别为表1中三种控制条件下某一典型值的振动荷载和不平顺振动波长的圆频率(i=1，2，3)，可表示为

Pi=M0αiωi

(3)

(4)

式中：M0为列车簧下质量；v为列车的运行速度；Li、αi分别为表1中三种条件下某一典型波长和对应的矢高(i=1，2，3)。值得说明的是，由于铁路线路在运营过程中受复杂环境及列车类型多样化的影响，在计算时应根据实际情况对典型波长所对应的矢高进行适当修正。

1.2 任意路基土体单元的竖向应力表达式

由上文分析可知，类似地对于任意深度z处的路基土体单元来说，将可能会承受来自路基填料的堆载、轨道结构自重和列车荷载三部分作用产生的竖向应力。但1.1节已对轨道结构自重做了简化，将其等效为某填料的堆载作用，故其所承受的竖向应力可表示为

σ1=σT+σD

(5)

式中：σT为路基填料堆载及轨道结构自重产生的竖向应力；σD为列车荷载产生的竖向动应力；σ1为深度z处土体所承受的竖向应力。

事实上，铁路在前期的填筑及后期的运营过程中，路基填料的堆载和轨道结构的自重均会对路基土产生竖向应力。但在铁路填筑期间，该部分作用是造成路基土体单元承受竖向应力的关键原因，此时竖向应力值的大小主要与填料的类型和堆积高度有关。为计算路基土中由填料堆载作用产生的竖向应力，现根据地基中的应力计算原理，对于在填筑及运营期间的路基土来说，任意深度z处的土体单元由填料堆载及轨道结构自重产生的竖向应力可定义为[24]

σT=γGh+γz=σG+γz

(6)

式中：γG为等效填料重度；h为轨道结构高度；γ为路基填料重度；z为计算点距填料顶面的高度；σG为轨道结构自重下的竖向应力。

而铁路在后期的运营过程中，路基土在一定深度范围内除了承受填料堆载和轨道结构自重的作用(σT)以外，还将承受来自列车引起的动应力(σD)影响。此刻，不同深度路基土所承受的动应力并不一致，且随着深度的增加在不断地减小[25]，其值与列车荷载作用力、综合动力影响系数和深度等因素均有关，可表示为

(7)

式中：a、b为拟合系数，通常对于无砟轨道，a取2.12，b取1.18；对于有砟轨道，a取0.64，b取0.86[25]；Φw为综合动力影响系数；Lw为路基面承受的动应力纵向影响距离；L1为转向架固定轴距；Bw为动应力传递至无砟轨道路基面横向分布宽。

综合以上分析，对于任意深度z处的路基土体单元来说，其所承受由填料堆载、轨道结构自重和列车荷载产生的竖向应力为

(8)

需要说明的是，在铁路填筑期间，仅需考虑填料堆载和轨道结构自重对路基土的影响，此时σT即为总的竖向应力；而在后期的运营中还需考虑列车荷载的影响，此刻任意深度z处的路基土体单元所承受总的竖向应力可由式(8)计算。由于本文研究的是铁路路基的长期沉降问题，不仅考虑了静载作用的影响，同时也考虑了列车动载作用产生的影响，故将利用式(8)进行主应力差表达式的推导。

1.3 考虑路基填料堆载和列车荷载下主应力差表达式的推导

由图2可知，Burgers模型是由Maxwell模型和Kelvin模型串联而成，故在推导Maxwell模型和Kelvin模型的沉降变形方程时，都需通过由路基填料堆载及列车荷载作用所建立的主应力差表达式进行展开。根据弹塑性力学原理，路基土在空间应力状态下，偏应力张量为

Sij=σij-σmδij

(9)

式中：Sij为偏应力张量；σij为路基土在空间应力状态下的应力张量；σm为球应力张量；δij为单位矩阵。

竖向偏应力为

(10)

式中：σ*=σ1-σ3为主应力差，此时，在路基填料堆载及列车荷载作用下，主应力差σ*也会随着时间t而发生变化，其表达式为

σ*(t)=σ1(t)-σ3=NQ(P0+P1sinω1t+

P2sinω2t+P3sinω3t)+σT-σ3

(11)

其中，N=1-z/(a+bz)，Q=4Φw/[(Lw+L1)Bw]。

1.4 考虑路基填料堆载和列车荷载下Maxwell模型沉降变形方程

Maxwell模型是由胡克体和牛顿体串联而成，力学模型如图2第1部分所示，其本构方程为[20]

(12)

式中：G1为Maxwell模型体的剪切模量；η1为Maxwell模型体的黏滞系数。

将式(11)代入式(10)得

P3sinω3t)+σT-σ3]

(13)

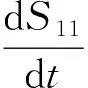
(14)

将式(13)和式(14)代入式(12)，再对时间t进行积分，同时代入初始条件当t=0时，e11=(σ1max―σ3)/3G1，整理可得

(15)

式中：e11为Maxwell模型在荷载作用下的竖向偏应变；σ1max为路基土中最大的竖向压应力。

由于荷载变化对球应变的影响不大[20]，且当球应变以t=0时刻的荷载值进行计算时，则有

(16)

式中：εm为球应变；K为体积模量。

因此，由式(15)和式(16)可得Maxwell模型在路基填料堆载和列车荷载作用下的沉降变形方程为

εⅠ=e11+εm=

(17)

式中：εⅠ为Maxwell模型的应变。

1.5 考虑路基填料堆载和列车荷载下Kelvin模型沉降变形方程

Kelvin模型是由胡克体和牛顿体并联组成，力学模型如图2第2部分所示，其表达式为

(18)

式中：G2为Kelvin模型体的剪切模量；η2为Kelvin模型体的黏滞系数。

将式(18)变形为

(19)

将式(13)代入式(19)并对其进行求解，届时代入初始条件当t=0时，Kelvin模型的偏应变e11=0，整理可得路基填料堆载和列车荷载下其变形方程为

(20)

式中：εⅡ为Kelvin模型的应变。

1.6 考虑路基填料堆载和列车荷载下Burgers模型铁路路基沉降变形方程

前面分别推导了路基土在填料堆载和列车荷载作用下Maxwell模型和Kelvin模型的沉降变形方程，由于Burgers模型是由Maxwell模型和Kelvin模型串联而成(见图2)，即

(21)

式中：σ为Burgers模型的应力；ε为Burgers模型的应变；σⅠ为Maxwell模型的应力；σⅡ为Kelvin模型的应力。

因此，根据式(17)、式(20)、式(21)可得图1所示路基填料堆载及列车荷载作用下Burgers模型的铁路路基长期沉降变形方程为

(22)

此时令

考虑到实际中路基的纵向长度很长，认为在受力变形中其水平方向的变形受限[26]，并令σ3=k0σ1，其中k0为土压力系数。因此，沿竖向积分可得距路基表面厚度为z的土层变形表达式为

(23)

式中：S(t)为路基土随时间变化的竖向沉降变形。

2 模型的验证

由于铁路路基的沉降发展，经历了上部结构层长期堆载作用，以及列车循环荷载加载过程。因此，分别采用路基填料堆载及列车荷载两种作用方式下路基实际的沉降数据，验证基于Burgers模型预测铁路路基长期沉降变形方程的合理性与准确性。

2.1 路基填料堆载下模型的验证

为了说明所推导的模型能适用于路基土在填料堆载作用下的沉降变形特性，现利用文献[26]中高速铁路粗粒土路基的沉降数据对方程进行验证。在计算过程中，基床表层、底层和路基本体层填筑高度均与文献保持一致，分别为0.4、2.3、2.0 m，且此时不考虑列车荷载作用(即方程中含有Pi项的算式均为零)，仅考虑路基各结构层中填料堆载及轨道自重等因素对路基沉降变形的影响。

曲线拟合法是确定路基长期沉降预测模型参数中较为广泛的一种方法。本文将分别利用模型试验中路基基床层、路基本体层和地基层的沉降数据，并基于优化粒子群算法原理，采用曲线拟合法对式(23)中的相关参数进行反演，其结果见表2。同时，得出了对应的时间-沉降曲线。图3～图5分别给出了采用本文模型计算路基基床层、路基本体层以及地基层的沉降结果，并与文献[26]和实测沉降数据进行对比。

由表2可见，参数的拟合相关性较高，相关系数R2均在0.98以上，要高于文献[26]中的研究成果，表明本次反演的结果可靠性较好。同时，值得说明的是，文献[26]的研究仅考虑了Kelvin模型，其所包含的参数为：体积模量K、剪切模量G和黏滞系数H。其在反演的过程中：基床层K为151.6 MPa、G为51.54 MPa、H为9 249 MPa·d；路基本体层K为105.3 MPa、G为35.81 MPa、H为7 371 MPa·d；地基层K为85.4 MPa、G为11.64 MPa、H为3 189 MPa·d。此时结合表2可以看出，本文反演的参数值与文献[26]的结果大小相仿，这说明本文反演拟合的参数均在土体参数的合理范围内。

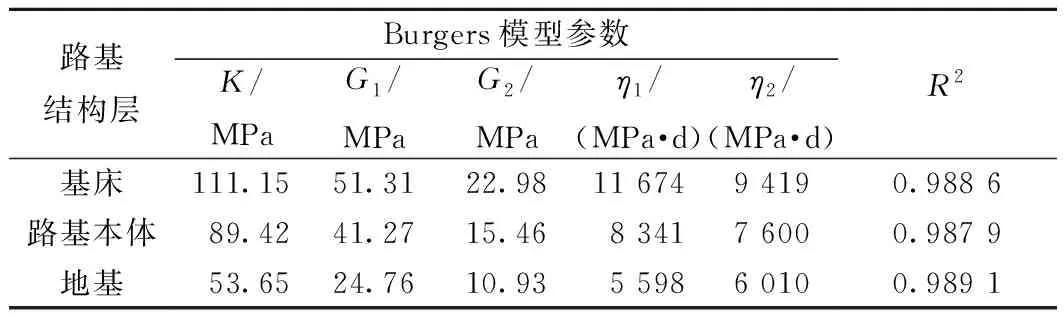
表2 路堤填料堆载下Burgers模型参数反演结果

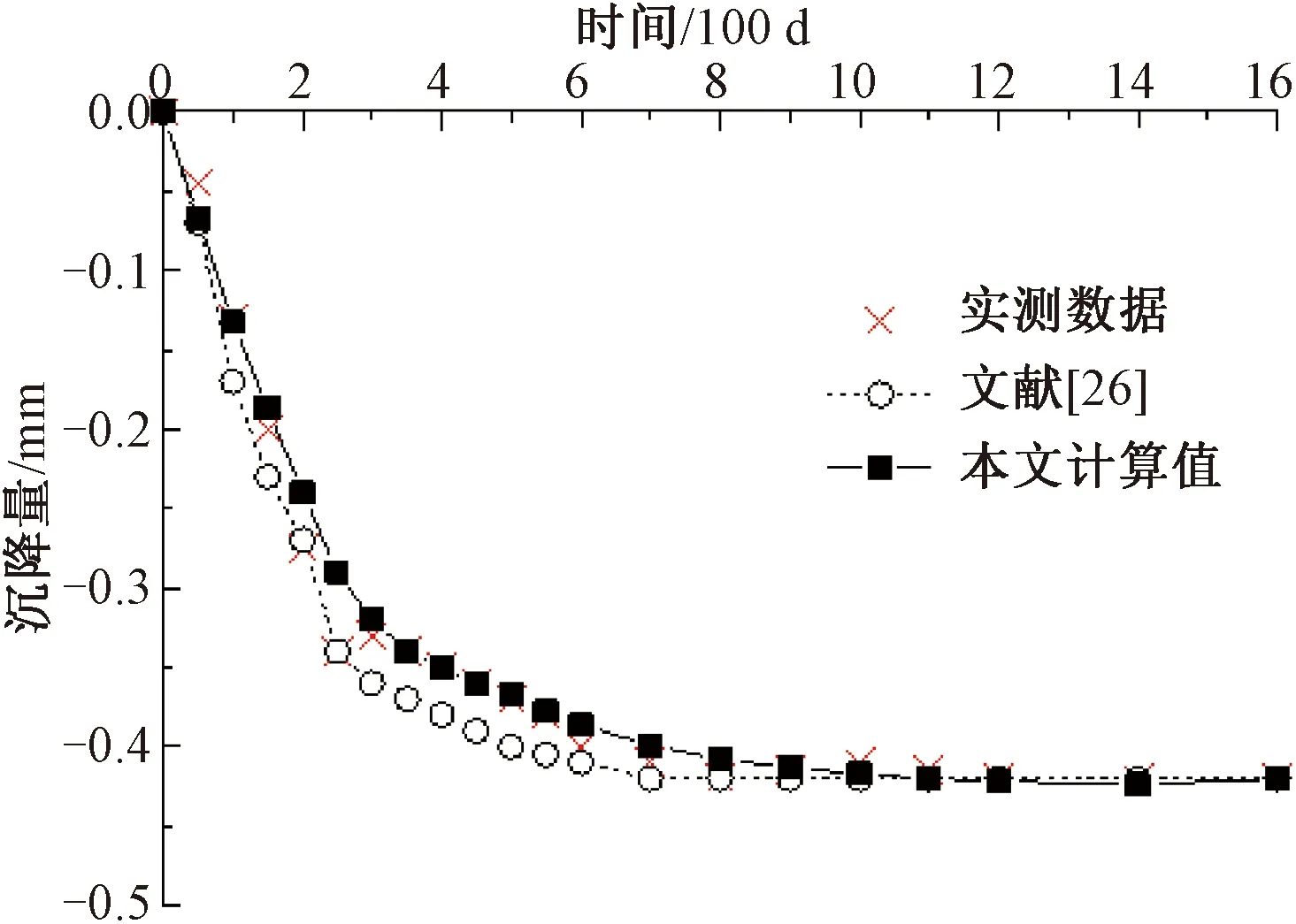
图3 基床层沉降变形拟合与文献及实测对比

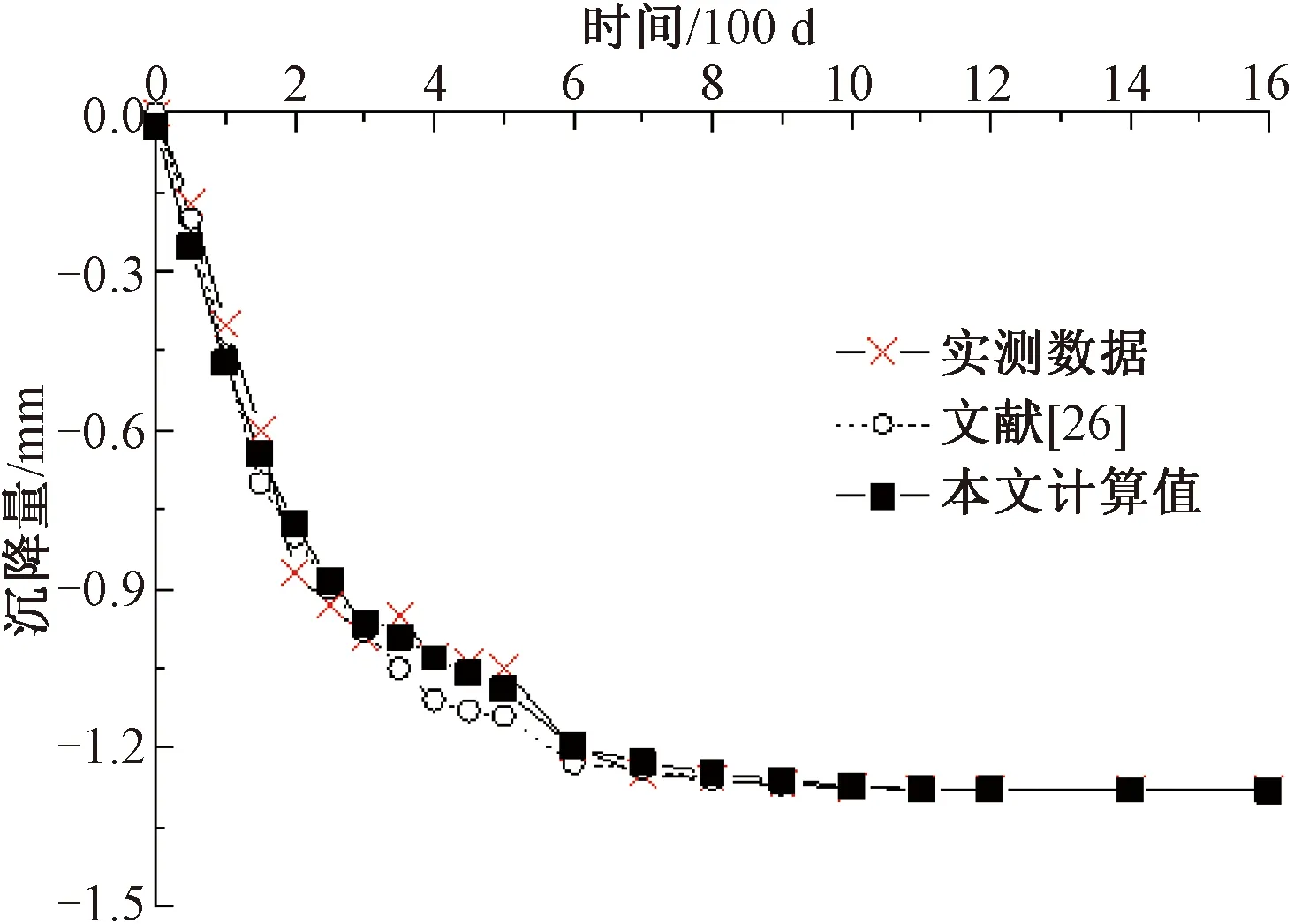
图4 路基本体层沉降变形拟合与文献及实测对比

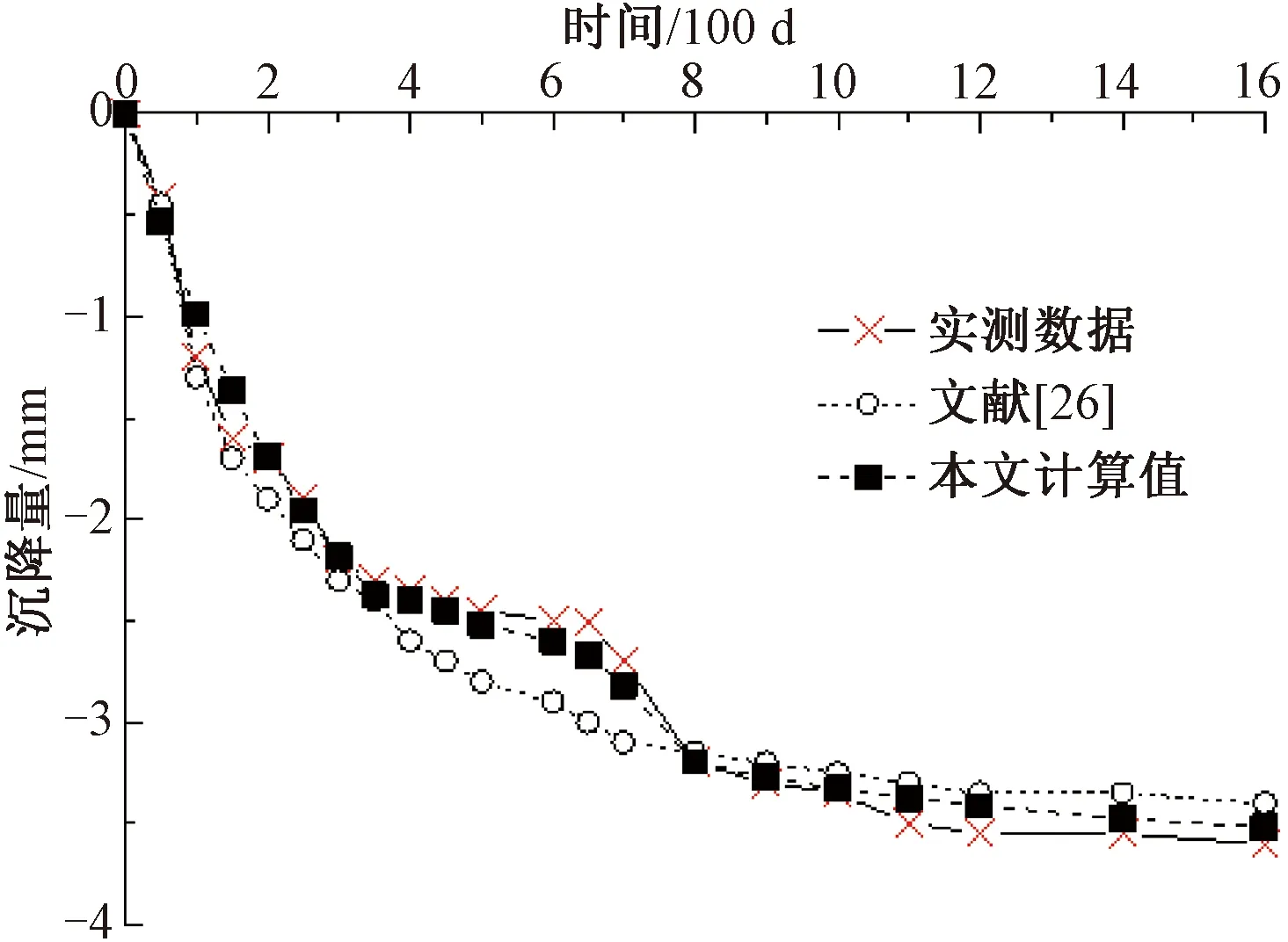
图5 地基层沉降变形拟合与文献及实测对比

进一步地，由图3、图4、图5可以看出，随着时间推移到300～800 d期间，文献[26]开始偏离实测曲线，而本文模型与实测曲线保持着相同的变化规律。本模型之所以在反演参数值相似的情况下，参数的相关系数以及与实测沉降曲线相比的吻合度都要略高于文献[26]的研究成果，可能是由本文多虑了Maxwell模型以及路基土所处的空间应力状态等原因造成，使得拟合结果更为精准。

现利用反演出的参数对高速铁路粗粒土路基的长期沉降进行预测。在路基填料堆载下，本模型预测结果与文献[26]中的计算结果以及路基实际沉降数据对比如图6所示。

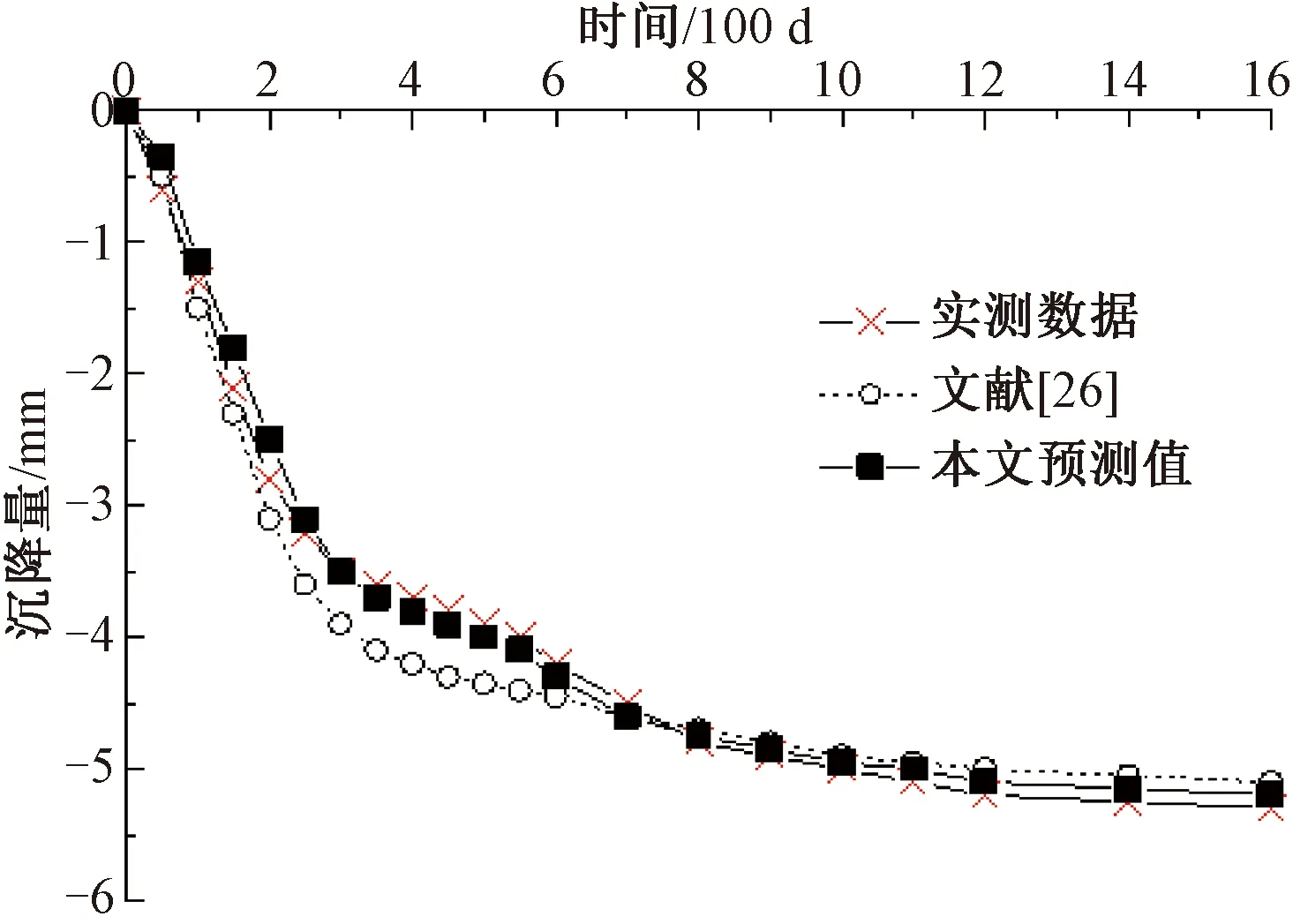
图6 路基沉降变形预测与文献及实测对比

由图6可知，本文的预测曲线同实测曲线的吻合度略高于文献[26]，同时，随着时间的变化，曲线呈现出先快后慢，最后趋于稳定的增长方式。这说明本模型预测铁路路基在填料堆载下的长期沉降变形趋势符合实际沉降变化规律，且对路基土变形特性具有较强的适应性。

2.2 列车荷载下模型的验证

进一步地验证本模型在列车动载作用下预测铁路路基长期沉降的优势，现对文献[27]中天津至保定客运专线试验段在列车荷载工况下路基的沉降算例进行分析。在计算路基沉降过程中，为了能够和文献中的计算结果进行有效地比较，本文采用与文献[27]一致的路堤填筑方式、尺寸及填料参数。同时利用文献[27]中列车荷载工况下路基的沉降数据对式(23)进行参数反演，反演结果见表3。此时，将反演出的参数、路堤几何尺寸及填料相关参数代入本模型进行计算，从而得到列车荷载作用下路基的沉降量并与文献计算结果作对比分析。图7给出了列车荷载作用下本模型计算结果与文献[27]计算结果的对比图。

由表3可知，在列车荷载作用下，模型参数的拟合相关性较高，相关系数R2接近0.99，说明本模型所反演出的参数值合理，具有较高的可靠性。同时，由图7可知，在0～3 a期间，虽然本模型计算路基的沉降量与文献计算结果有微小的偏差，但两曲线的总体吻合良好；随着时间的变化，沉降量的增长方式同样符合先快速增大后趋于稳定的变化规律，模型与文献计算路基最终沉降量分别为885、872 mm。通过此次验证结果表明，本模型计算路基在列车荷载作用下的沉降时，对路基土的沉降变形特性同样具有较强地适应性。

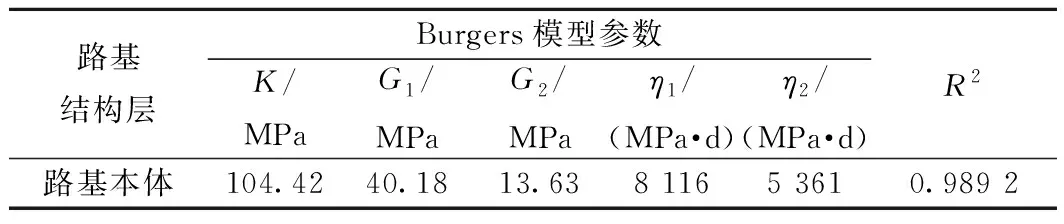
表3 列车荷载下Burgers模型参数反演结果

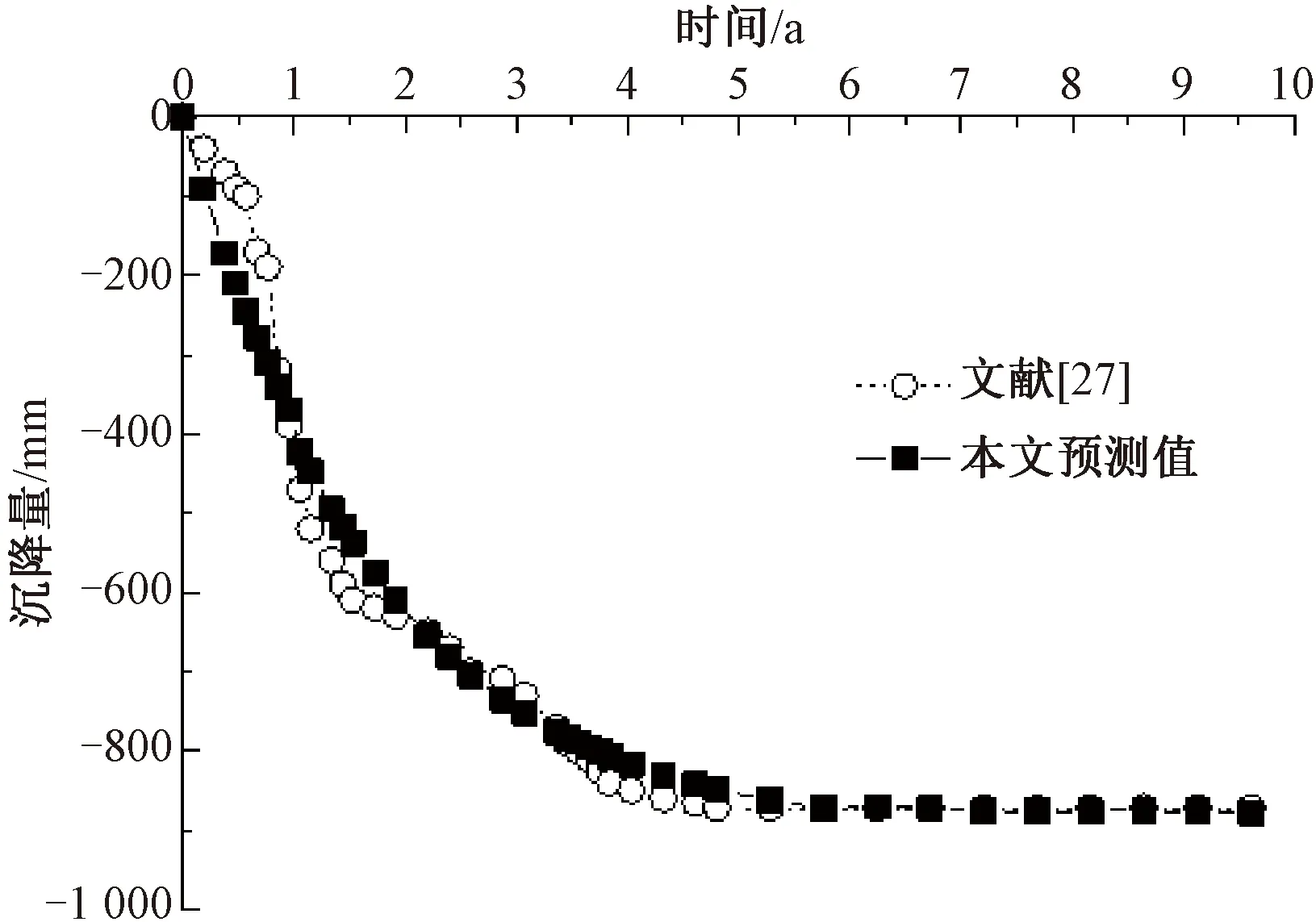
图7 路基沉降变形计算与文献对比

结合上述验证结果可知，本模型均能较好地反映铁路路基在填料堆载及列车荷载作用下长期沉降变形特性，说明本文所推导模型方程的合理性及准确性较高。但从图6和图7的结果也可以看出，在预测初始阶段，本文计算结果与文献数据的吻合度较低，文献中路基沉降衰减阶段持续时间更短，变形速率更快。因此，对于如何有效提高模型前期精确度还需做进一步地研究探讨。

3 结论

本文基于Burgers模型，在充分考虑铁路路基填筑及列车运营期间路基土所处的空间应力状态及蠕变特性的基础上，通过选取合适的荷载表达式，建立了在路基填料堆载及列车荷载作用下路基土主应力差随时间变化的关系式，从而推导出预测铁路路基长期沉降变形方程。进一步地，利用现有文献结果及实测数据确定参数并代入模型计算，分别验证了模型预测路基土在填料堆载和列车荷载作用下的沉降变形规律。现得出以下结论：

(1)本文所建立的模型是基于Burgers模型的分解，充分考虑了路基土在填料堆载和列车荷载作用下所处的应力状态及其自身蠕变特性的影响，从任意路基土体单元的主应力差表达式出发，分别推导出Maxwell模型和Kelvin模型的沉降变形方程，进而建立了基于Burgers模型的铁路路基沉降变形方程，用于路基长期沉降的预测分析。

(2)本模型均能较好的反映路基土在填料堆载及列车荷载作用下沉降量随着时间的变化呈先快后慢，最后趋于稳定的规律，表明模型对路基土在填料堆载及列车荷载作用下的沉降变形特性均有较强的适应性。

(3)本模型参数均在土体参数合理范围内，且预测路基长期沉降所得结果可靠性和精确度较高，可为类似工程提供一定的参考。