单线铁路成对追踪平行运行图通过能力计算方法研究

赵 鹏，童有超，张进川，宋文波，马铭瑶

(1.北京交通大学 交通运输学院，北京 100044；2.中国铁路成都局集团有限公司 成都北车站，四川 成都 610500)

当前，存在于我国西北高原地带的部分单线铁路干线，如青藏铁路格拉段、南疆铁路等的运输能力已难以满足逐年增长的运输需求，需对其进行扩能改造。但既有的运输组织优化类扩能措施如：运行图调整、中间站会让方式优化等难以取得良好的扩能效果，传统的工程改造类扩能措施如：修建复线、增设会让站等，受限于高原地带的恶劣的自然环境，使得工程施工难度大、工期长、费用高。因此，亟需探求新的扩能手段以解决该部分线路运输能力不足问题。移动闭塞作为当下最为先进闭塞制式，能有效缩短列车追踪运行间隔，提高线路通过能力，且我国正在国家科技项目支持下自主研发的新型列车控制系统为铁路实现移动闭塞提供了可能，因此本文以应用移动闭塞为单线铁路扩能手段，对移动闭塞下单线铁路的能力问题展开研究。单线铁路应用移动闭塞后，宜采用单线追踪运行图作为日常行车组织工作的基础。为此，本文以单线铁路成对追踪平行运行图为研究对象，提出该类运行图在正常运输场景下的通过能力计算模型。

当前，计算单线平行运行图通过能力常采用人工计算法，即从困难区间开始逐步调整各相邻车站的列车交会方式使得运行图周期达到最小[1]。但对中间站较多或有多个技术作业站的单线铁路而言使用人工计算法较为繁琐，而且容易因人工调整列车交会方式不周而得不到正确的最小列车运行图周期，从而计算出错误的线路通过能力。为此，严余松[2-3]较早地提出求解单线成对非追踪平行运行图最小周期的整数规划模型及求解算法，并在此基础上进一步结合遗传算法改善前期研究，提高求解速度。郑亚晶等[4]构建求解单线铁路成对非追踪平行运行图最小周期时间的混合整数非线性规划模型，该模型的计算结果能直观展现出列车在各区间的交会方案。史峰等[5-6]构建了单线铁路列车运行图排序模型，并设计相应的时间循环迭代优化求解方法，该方法将运行图铺画模型分解为多个阶段模型，以冲突最优为目标求解各个阶段模型，再以阶段优化结果为基础，周而复始按时间循环迭代进行整体优化以求出整体最优解。纪加伦等[7]从行车组织角度初步探讨了我国铁路应用移动制度下的区间通过能力计算方法。Li 等[8-9]在考虑了列车延误程度和上下行列车数量不均衡程度的基础上，构建了单线铁路通过能力计算的0-1混合整数规划模型，并设计相应的启发式算法进行仿真求解。综上，既有的单线运行图通过能力计算研究较少考虑列车追踪运行，有必要对该部分内容进行补充完善。

本文依据单线运行图的特点，在详细分析单线成对追踪运行图可能的列车交会模式及其组合后形成的区间运行图铺画方案的基础上，以单线成对追踪运行图最小周期时间最小化为目标，构建考虑相邻区间运行图铺画方案衔接关系的单线成对追踪运行图最小周期时间计算的混合整数线性规划模型，并使用Lingo12对实际算例进行求解以验证模型的可靠性和实用性。

1 单线成对追踪运行图可能的列车交会模式

n为单线铁路区段车站数，则此区段包含n-1个区间，从该区段下行方向起点站开始对车站依次编号，结果为1，2，3，…，n，i为车站序号，(i,i+1)为区间。

依据车站位置以及上下行列车在车站是否有技术作业，单线成对追踪运行图共有8种列车交会模式，可分为4类情形，见图1～图4。

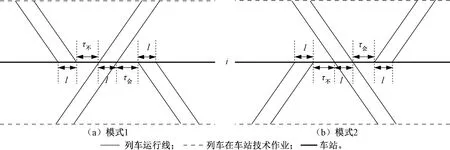
图1 上下行列车在中间站均无技术作业时的列车交会模式

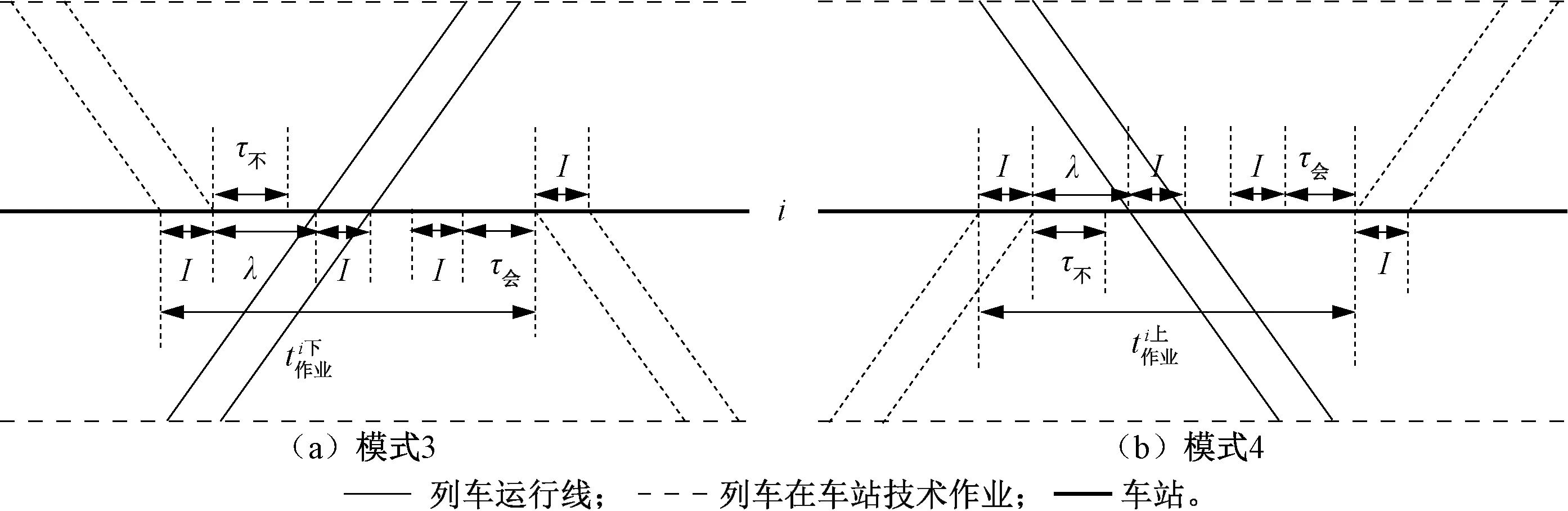
图2 上行或下行列车在中间站有技术作业时的列车交会模式

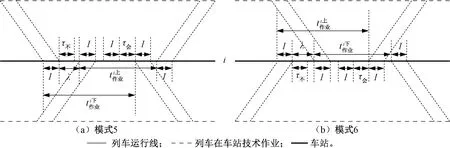
图3 上下行列车在中间站均有技术作业时的列车交会模式

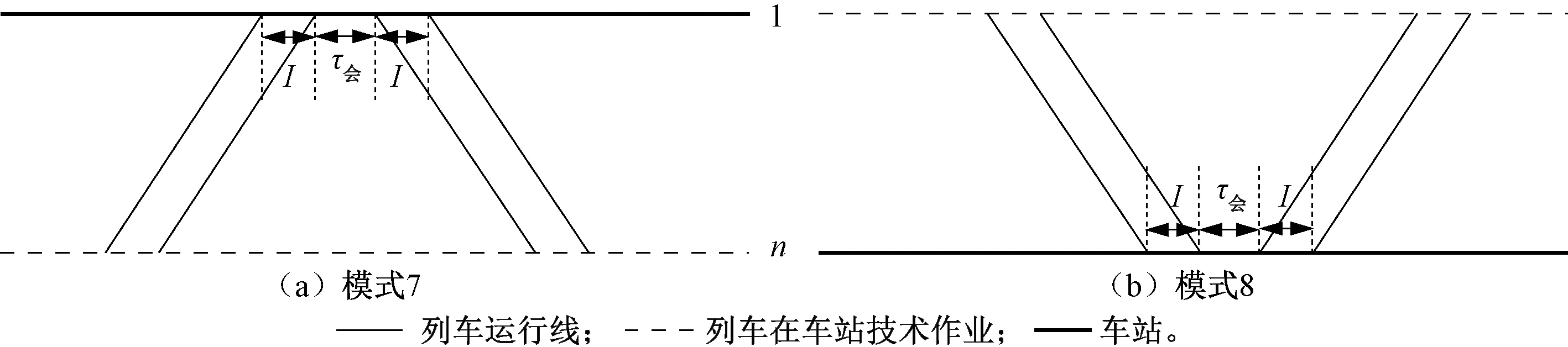
图4 上下行列车在区段首末站的列车交会模式

1.1 上下行列车在中间站均无技术作业

当上下行列车在中间站均无技术作业时，列车在中间站的交会模式共有两种：下行列车停站、上行列车通过，见图1(a)；上行列车停站、下行列车通过，见图1(b)。图中：I为列车追踪间隔时间，min；τ不为不同时到达间隔时间，min；τ会为会车间隔时间，min。

1.2 上行列车或下行列车在中间站有技术作业

考虑实际情况(一般有列车技术作业时间t技≥2I+τ不+τ会)，当只有下行列车在中间站有技术作业时，此时上下行列车在中间站的交会方式只有一种，即下行列车停站上行列车通过，见图2(a)；反之，当只有上行列车在中间站有技术作业时，此时上下行列车在中间站的交会方式也只有一种，即上行列车停站下行列车通过，见图2(b)。

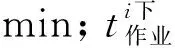
1.3 上下行列车在中间站均有技术作业

当上下行列车在中间站均有技术作业时，按照上下行列车到达中间站的次序，上下行列车在中间站的列车交会模式可分为2种：即下行列车先到，上行列车后到见图3(a)，以及上行列车先到，下行列车后到见图3(b)。

1.4 上下行列车所到车站为区段端点站

当上下行列车所到车站是区段端点站时，按车站的位置，上下行列车交会模式可分为2种：即列车在区段首站的交会模式见图4(a)；列车在区段末站的交会模式见图4(b)。

2 单线成对追踪平行运行图最小周期计算

对单线区段上任意区间(i,i+1)，其追踪平行运行图周期T见图5，计算式为

(1)

由图5可知，计算区间追踪平行运行图周期必须考虑上下行列车在区间两端车站的交会模式。以下依据实际情况(一般不存在区间两端车站均为技术站的情况，因此该情形本文不予考虑)，对上述8种列车交会模式进行组合得出所有有效的区间追踪平行运行图铺画方案并对每一个铺画方案做出详细分析。

图5 单线成对追踪平行运行图周期结构示意图

2.1 区间两端车站均为中间站且列车在车站均无技术作业

当列车在区间两端车站均无技术作业时，此时列车在区间两端车站的交会模式只能从模式1、模式2选择，组合起来共有4种区间运行图铺画方案即：列车在车站i和i+1的交会模式均为模式1，列车在车站i的交会模式为模式1在车站i+1的交会模式为模式2，列车在车站i的交会模式为模式2在车站i+1的交会模式为模式1，列车在车站i和i+1的交会模式均为模式2，依次将此4种铺画方案命名为方案1、2、3、4，见图6。

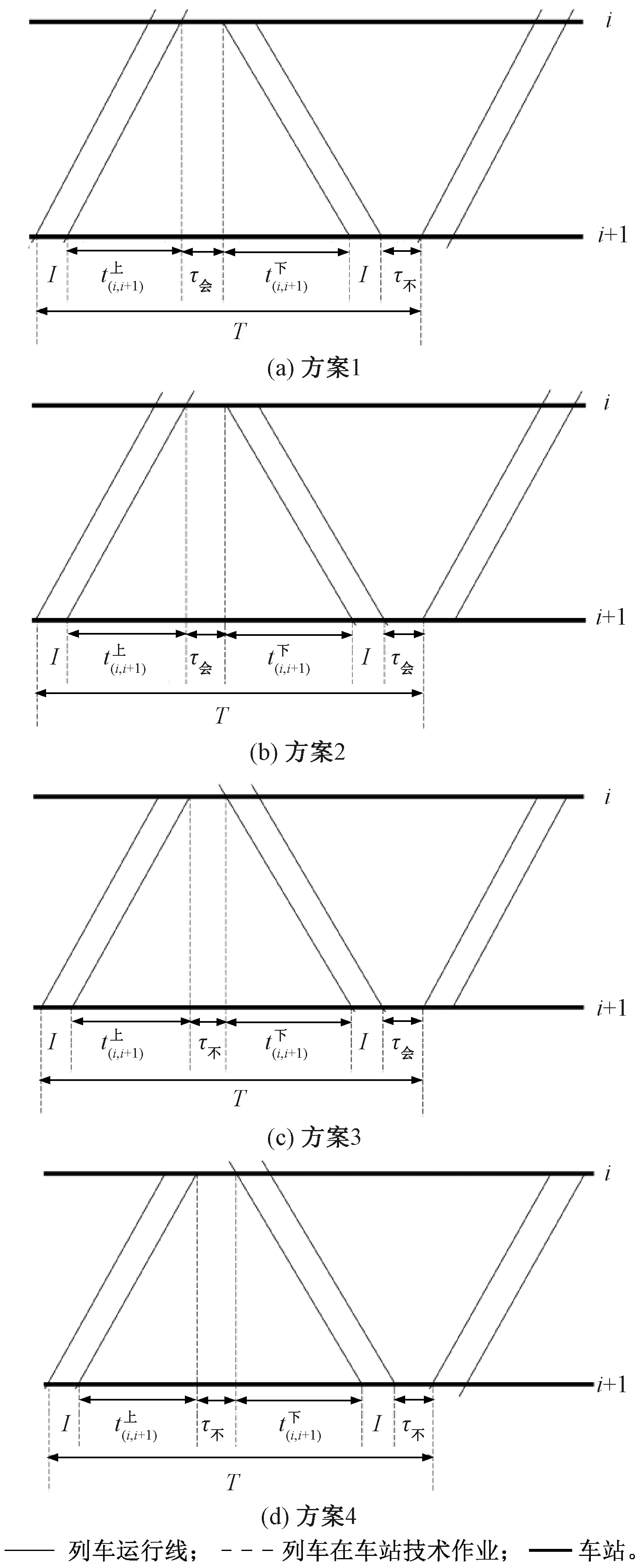
图6 区间两端车站均为中间站且列车在两车站无技术作业时的区间追踪平行运行图铺画方案

上下行列车在车站使用不同的交会模式，会导致车站间隔时间τi以及列车在车站的起停附加时分之和ti发生改变，从而改变区间运行图周期，表1对比展示了图6中4种运行图铺画方案下的区间运行图周期的变化,其中没有发生改变的部分归类到表中的“不变成分”，发生变化的部分归类到“变化成分”并对其对其各项内容做详细展示，下同。

表1 区间两端车站均为中间站且列车在车站无技术作业时的4种区间追踪平行运行图周期差异

2.2 区间两端车站均为中间站且下行列车在其中一车站有技术作业

依据在区间一端车站进行技术作业的列车种类，可将有技术作业的情形划分为3类子情形即：下行列车在区间两端车站其中之一有技术作业，上行列车在区间两端车站其中之一有技术作业，上、下行列车在区间两端车站其中之一有技术作业。同2.1节，依次对三类子情形下可选交会模式进行组合，得到对应的运行图铺画方案(分别见图7～图9)，并对不同铺画方案下的运行图周期进行对比(分别见表2～表4)，其中表4中的“新增成分”指的是采用该情形下的某种铺画方案，计算区间运行图周期需额外增加的时间。

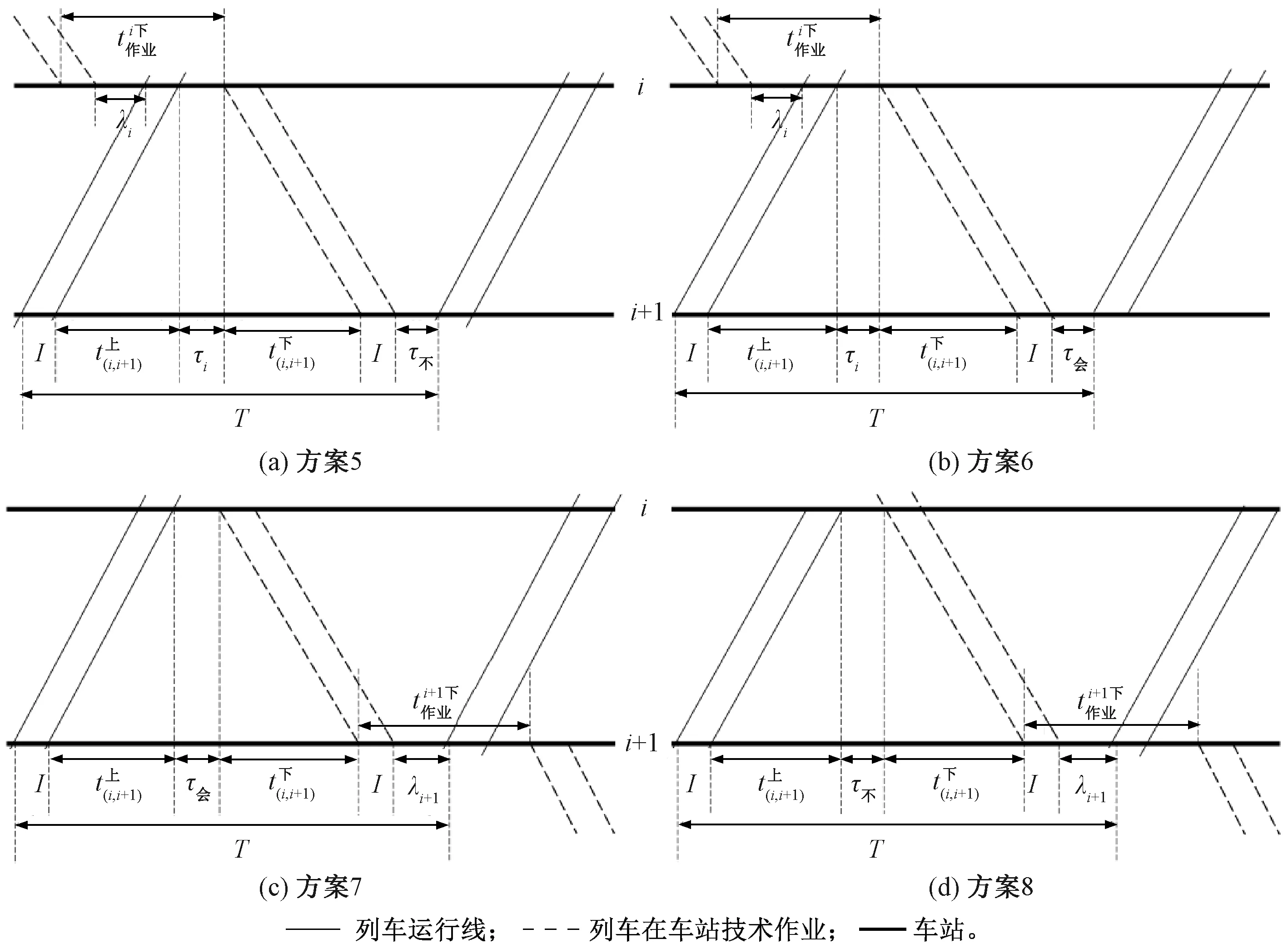
图7 区间两端车站均为中间站且下行列车在其中一有技术作业时的区间追踪平行运行图铺画方案

图8 区间两端车站均为中间站且上行列车在其中一车站有技术作业时的区间追踪平行运行图铺画方案

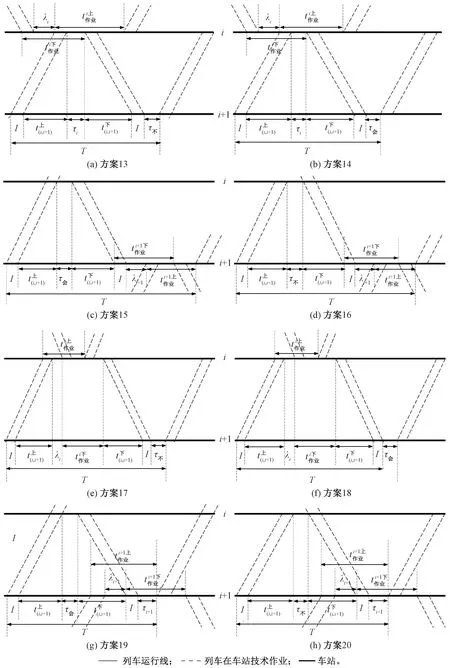
图9 区段两端车站均为中间站且上下行列车在其中一车站有技术作业时的区间平行运行图铺画方案

表2 区间两端车站均为中间站且下行列车在其中一车站有技术作业时的4种区间追踪平行运行图周期差异

表3 区间两端车站均为中间站且上行列车在其中一车站有技术作业下4种区间平行运行图周期差异

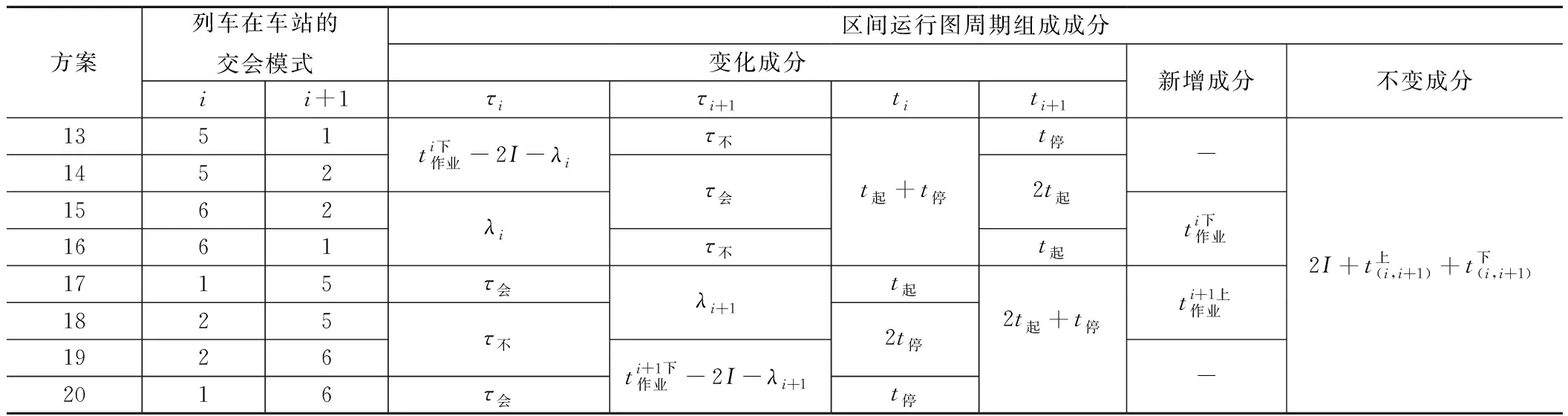
表4 区间两端车站均为中间站且上下行列车在其中一车站有技术作业时的8种区间平行运行图周期差异

2.3 区间一端车站为区段首末站

同理，考虑该情形下的可选交会模式，对其进行有效组合，得到对应的运行图铺画方案，并对比分析该情形下不同铺画方案的运行图周期,见表5。

表5 区间一端车站为首末站时的4种区间平行运行图周期差异

综上可知，单线区间成对追踪运行图铺画方案共有24种，可被分为5个类别，见表6。

表6 单线区间成对追踪运行图铺画方案类别及内容

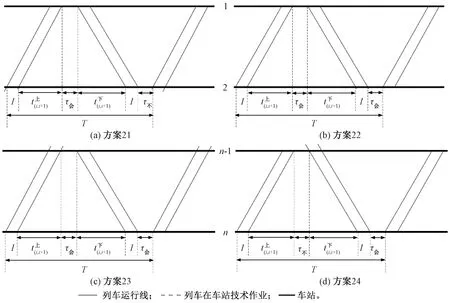
图10 区间一端车站为首末站时的区间平行运行图铺画方案

3 模型构建

模型在已知车站间隔时间、起停附加时分、列车技术作业时间、区间运行时分等运行图参数的情况下，考虑相邻区间运行图铺画方案之间的衔接关系，通过不断调整各区间运行图铺画方案以及上下行列车在技术站的到达间隔，使单线成对追踪运行图最小周期时间达到最优。

3.1 决策变量

3.2 目标函数

使单线区段成对追踪平行运行图周期T周最小。

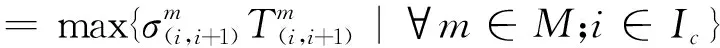
(2)

3.3 约束条件

(1)唯一性约束：单线区段上的每个区间只能选择一种运行图铺画方案。

(3)

(2)当区间一段车站为区段首末站时，只能选择图10中的运行图铺画方案。

(4)

(5)

(3)当列车在区间一端车站有技术作业时，λi需要满足以下约束：

(6)

(7)

(8)

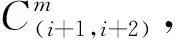
表集合的元素

由此可得以下约束

m∈Mi∈Ic

(9)

(10)

m∈Mi∈Ic

(11)

(12)

4 算例分析

本文以文献[1]376页例5-2-1的单线区段以及文献[7]的列车追踪间隔时间数据为算例，使用所提出的数学模型计算该单线区段的通过能力，算例数据见表8。

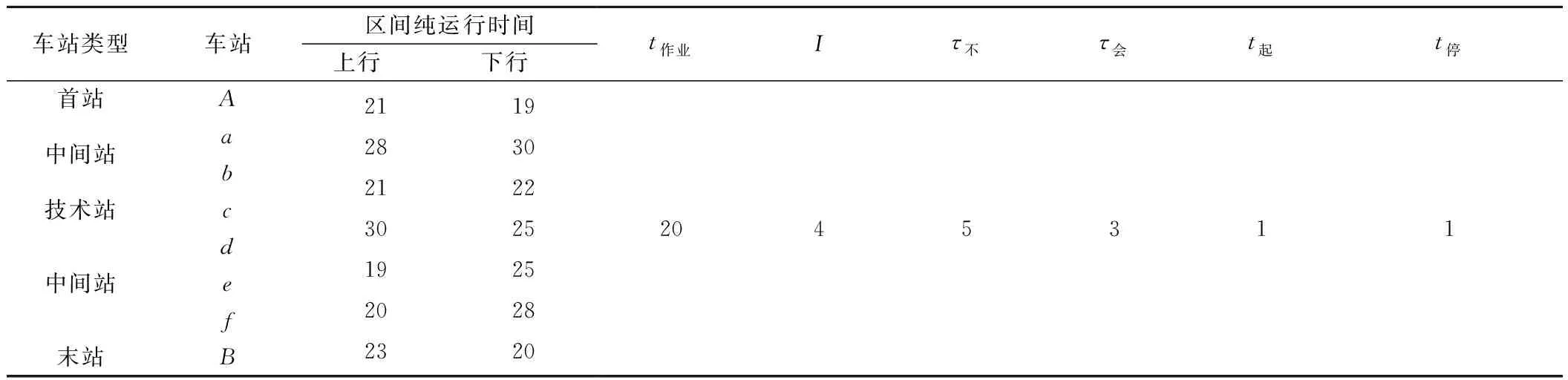
表8 运行图参数数据 min

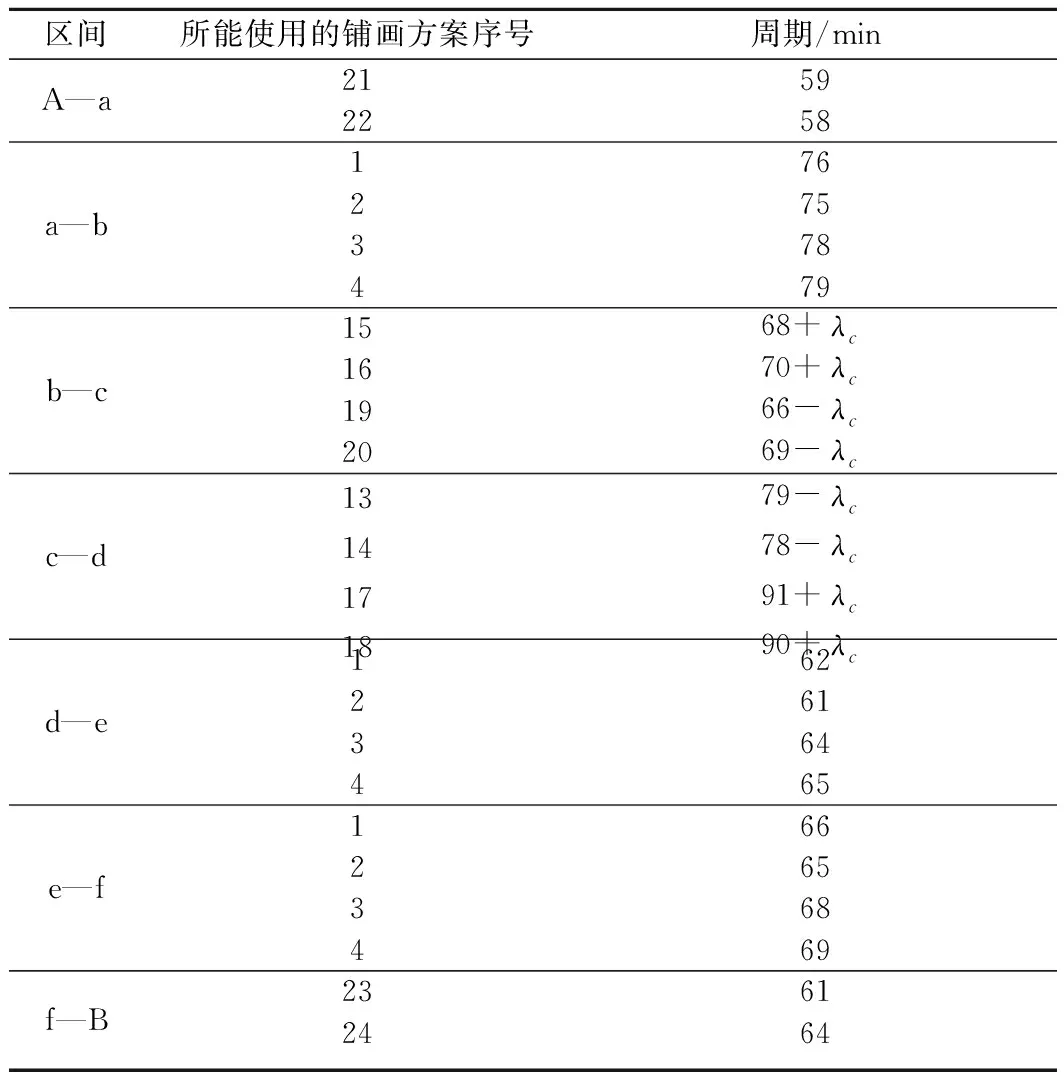
表9 各区间所能使用的铺画方案及其周期

为保证模型求解过程得每一步搜算均为可行解以提高求解效率，依据表6对该算例各区间所能采用的铺画方案进行总结，结果见表9。

使用商业软件Lingo12对上述模型进行求解，结果如下：

由此可知，区间(a,b)为算例的限制区间，因此该单线区段成对追踪平行运行图的周期为76 min。由此可得该单线区段成对追踪运行图的通过能力为

(13)

式中：n平为单线成对追踪运行图通过能力，对；t天为天窗时间，此处取120 min；T周为单线成对追踪运行图周期，min；n周为一个运行图周期内所包含的列车对数，对。

根据文献[4]可知，站间闭塞条件下，该单线区段成对非追踪平行运行图的周期为66 min，代入式(13)可得该条件下单线区段的通过能力为20对。由此可知，在应用移动闭塞后，该单线区段的通过能力可提升72.5%。

5 结束语

随着我国经济的快速发展，各区域之间的人力与物资交流愈发频繁，对铁路干线的通过能力提出了更高的要求，本文以移动闭塞为解决手段，提出了单线铁路成对追踪运行图最小周期时间的混合整数线性规划模型，完善了既有单线研究较少涉及移动闭塞、追踪运行的不足，具有一定的理论意义，同时算例结果验证了移动闭塞能较大幅度提高单线铁路通过能力，为单线铁路未来的发展方向提高一定参考，具有较强的现实意义。