通过辅助变流器降低电力机车注入牵引网电流谐波的方法

慕玫君，刘诗慧，林 飞, 张润泽，杨中平

(北京交通大学 电气工程学院， 北京 100044)

现代交流传动技术已广泛应用于电力机车及高速动车组，在运行过程中，牵引传动系统产生开关频率整数倍附近的中、高频谐波电流，容易与牵引网产生耦合谐振，使牵引网产生较大的电压波动，严重时将影响铁路系统的安全稳定运行。2007年7月，京哈线蓟县南变电所供电区段发生谐振事故，造成所亭电气设备烧损，谐振频率为750～1 150 Hz；2013年11月某机车经过京九线阜阳—向塘间多区段时，主断过压跳保护，高压电气设备烧损，经检测谐振频率为2 650 Hz。近年来发生谐振时其频率范围为750～2 750 Hz，谐振事故对机车及所在线路设备产生了较大的影响[1-3]。

此外，因各种非理想因素，四象限变流器交流侧仍存在3、5、7等奇次低次谐波，将对电能质量产生较大影响[4]，缩短电气化铁路设备寿命。

电气化铁路中常用的谐波抑制方案可包括地面设备集中补偿以及车载谐波补偿，而地面设备集中补偿包含无源谐波补偿及有源谐波补偿。LC滤波器以及高通滤波器常被用于电气化铁路滤除特定次谐波，以解决车网谐振问题[5-7]。有源滤波方案即基于电力电子技术，将变流器安装在牵引变电所以动态补偿谐波电流，可通过降压变压器加装有源滤波器, 也可采用级联H桥型拓扑直接挂网[8-12]。地面补偿方案均需要对现有的地面线路进行改造，通过加装电容电感或变流器等方式改变线路的阻抗特性，建造成本较高。

车载滤波方案中，无源滤波结构简单，容易实现，但其滤波频率单一，谐振频率变化时滤波效果不理想[13]；加装车载有源滤波器能够实现谐波电流的动态跟踪补偿，但增加了机车的体积与重量，不利于轨道交通的轻量化[14-15]；利用单相电力电子变压器改善电能质量的方法，减小了车载变压器的体积，但功率器件较多，系统稳定性及可靠性降低[16]。

针对牵引变流器产生的3、5、7等低次谐波及中高次谐波，本文提出一种通过辅助变流器谐波抑制控制方案。该方案针对辅助电源从辅助绕组取电的电力机车，通过检测原边谐波电流来计算指令电流，实现电流跟踪控制，控制辅助侧变流器完成单位功率因数整流功能的同时跟踪谐波电流指令，产生补偿电流注入交流测，从而抑制牵引变流器产生的谐波电流通过变压器注入接触网，避免谐振事故的产生。

通常情况下，常用IGBT模块的工作频率不超过5 kHz，难以产生850 Hz乃至更高频率的补偿电流，且损耗较大；而近年来出现的SiC器件，以其开关频率高、损耗小等优点，可将其应用于车载变流器，具有广阔的应用前景[17-18]。SiC器件与同一等级的Si器件相比，损耗减小30%，且工作于30 kHz时损耗仍小于Si IGBT工作于5 kHz时的损耗[19]；其较高的开关频率可实现本文的谐波抑制方案。本方案不需要加额外硬件电路，可实现谐波电流的动态补偿，受线路及机车参数变化影响较小。

1 辅助四象限变流器的谐波抑制原理

1.1 主电路图及工作原理

图1为电力机车牵引变流器及辅助变流器结构图，左侧为电气化铁路接触网，变压器牵引侧、辅助侧分别为牵引变流系统与辅助供电系统。牵引变流系统包括单相PWM整流器、牵引逆变器及牵引电机。辅助变流器通过牵引变压器的辅助绕组获取电能,并通过辅助变流器将其转换为三相交流电供车上空调、照明等设备使用。ip为原边电流，is为牵引绕组电流之和，ic为辅助绕组电流之和，变压器原边、牵引侧、辅助侧绕组的匝数分别为n1、n2、n3。图2为牵引变压器的等效电路图，vp、ip、vs、is、vc、ic分别为原边、牵引绕组、辅助绕组电压、电流，图中标注均为折算到辅助侧的值。

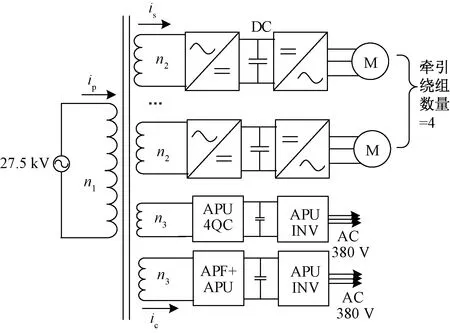
图1 机车牵引传动系统框图

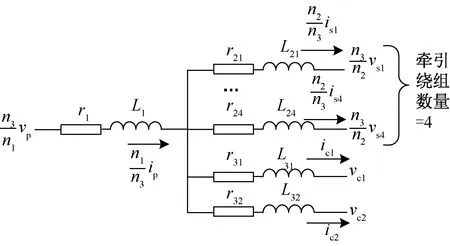
图2 牵引变压器等效电路

由图2可知

( 1 )

则

n1ip=n2is+n3ic

( 2 )

对于谐波电流有

n1iph=n2ish+n3ich

( 3 )

式中：ish为牵引变流器产生的谐波电流；iph为注入原边的谐波电流；ich为辅助变流器产生的谐波补偿电流。

针对牵引变流器产生的特征谐波，辅助侧四象限变流器于交流侧产生相应的补偿电流ich，使得iph→0，达到抑制原边谐波电流的目的。

1.2 谐波抑制功能对辅助变流器的影响

辅助四象限变流器实现单位功率因数整流的同时还要抑制原边谐波电流,必然会导致辅助四象限变流器电流峰值的增加。假定辅助绕组电流由基波电流和某次补偿电流两部分组成：ic1为50 Hz基波电流，ich为第h次谐波电流。

ic=ic1+ich

( 4 )

ic1=Acos(ω1t+α)

( 5 )

( 6 )

( 7 )

式中：A为基波电流幅值；ω1为基波角频率；ωh为谐波角频率；λn1|iph|/n3为谐波电流最大值；λ为补偿系数；|iph|为原边谐波电流幅值；α、β为初相角。

含有补偿电流的辅助绕组电流峰值为A+λn1|iph|/n3，有源滤波算法的加入增大了电流幅值，对器件选型提出了新的要求，器件额定电流大于2(A+λn1|iph|/n3)。

此外，辅助变流器交流侧电感对其整流功能及谐波补偿能力均有较大影响。电感过大将削弱注入原边的补偿电流，降低谐波电流指令跟踪能力，从而影响原边谐波电流抑制效果；电感过小将增大电流纹波，影响电能质量。因此该方案的电感需要根据控制算法的需要进行选择与设计。

2 辅助绕组电感参数设计

辅助变流器的谐波抑制功能要求其产生与原边谐波电流幅值相等的补偿电流，即对电流指令的跟踪性能提出了更高的要求，电感的取值对电流跟踪性能有较大影响；同时，辅助变流器还需完成单位功率因数整流的功能，此时电感取值也有一定限制，其大小与谐波电流变化率、开关频率、电流幅值等参数有关。图3为四象限变流器的电路拓扑，其中R3数值较小，可忽略。

图3 四象限变流器电路拓扑

2.1 考虑整流功能及纹波性能的电感取值

考虑四象限变流器单位功率因数整流[20]，电感的取值为

( 8 )

式中：Ud为直流侧电压；Um为交流电压峰值；Im为交流电流峰值。

同时，按照交流侧电流纹波不超过10%的约束[21]，有

( 9 )

式中：fs为开关频率；s为开关函数。

2.2 考虑电流跟踪性能的电感取值

辅助绕组交流侧电感电流沿指令电流呈锯齿状波动，如图4所示。

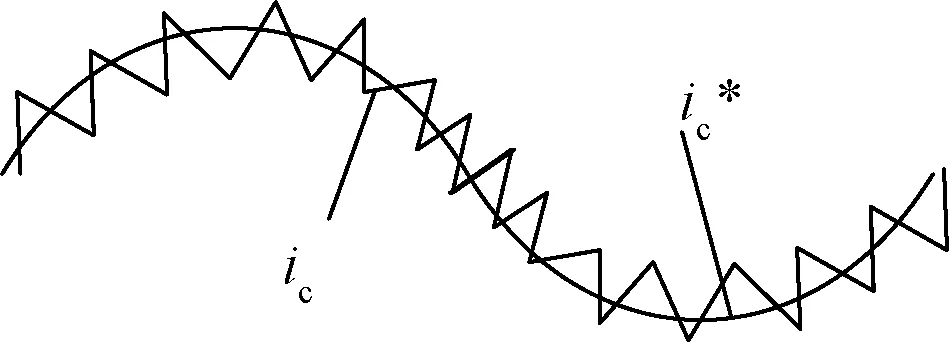
图4 指令电流跟踪原理

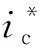
(10)

式中：iL3为电感电流；uc为辅助绕组两端电压。

由式(10)可知，若L3过大，电感电流的斜率较小，补偿电流的跟踪性能较差。

由文献[22]可以得到四象限变流器产生的谐波电流为

iN(t)=

(11)

式中：M为调制度；Ud2为牵引四象限变流器的直流侧电压；L2为牵引变流器交流侧电感；ωc为开关角频率；m、n为系数；Jn(mπM/2)为贝塞尔函数系数。

为保证电感电流能实时跟踪谐波电流指令，电感电流变化率大于谐波电流变化率。

(12)

(13)

电感的取值范围为

(14)

综合考虑有源滤波功能要求的指令电流跟踪性能，变流器单位功率因数整流功能及交流侧纹波特性，最终电感取值范围为

(15)

某型电力机车主电路参数见表1。

表1 主电路参数

对于牵引变流器产生的850～2 550 Hz的谐波电流，若辅助变流器开关频率为20 kHz[23]，电感的取值范围参见式(16)，此时辅助变流器对该范围内的谐波电流指令有较好的跟踪效果。当开关频率为5 kHz，电感取值范围参见式(17)。

21 μH≤L3≤105 μH

(16)

84 μH≤L3≤105 μH

(17)

3 谐波抑制控制策略

3.1 谐波抑制控制策略原理

由第1节分析可知，辅助绕组电流不仅包含基波电流，也包含牵引变压器产生的谐波补偿电流，因此辅助变流器控制环的指令电流也包含基波、谐波指令两部分。图5为辅助变流器谐波抑制控制方法的系统框图，直流电压控制器保证直流侧输出电压恒定，并产生基波电流参考幅值，谐波电流指令计算及基波电流指令计算分别用于产生谐波及基波的指令值。

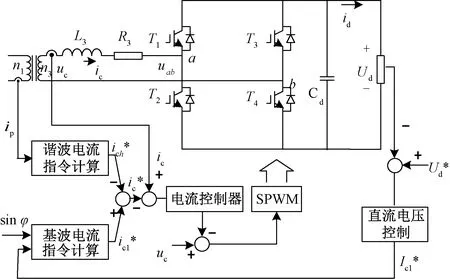
图5 辅助变流器谐波抑制控制方法系统框图

图6 电流环控制框图

3.2 指令电流计算及分析

为同时实现单位功率因数整流与有源滤波功能，辅助变流器需要对基波与谐波电流指令进行计算。

基波电流指令通过PI控制器得到，其计算公式为

(18)

式中：Kp为比例系数；Ti为积分系数

谐波电流检测是有源滤波功能实现的重要环节，通过检测原边电流，提取出谐波电流指令，从而控制变流器产生与其等大反向的补偿电流。本文采用滑窗傅里叶变换的方法，其傅里叶变换公式为

(19)

(20)

(21)

式中：N为窗口长度；xnew为新的数据点。当n=1，提取出电流基波，谐波电流即为原边电流减去基波电流。滑窗离散傅里叶分析框图如图7所示。

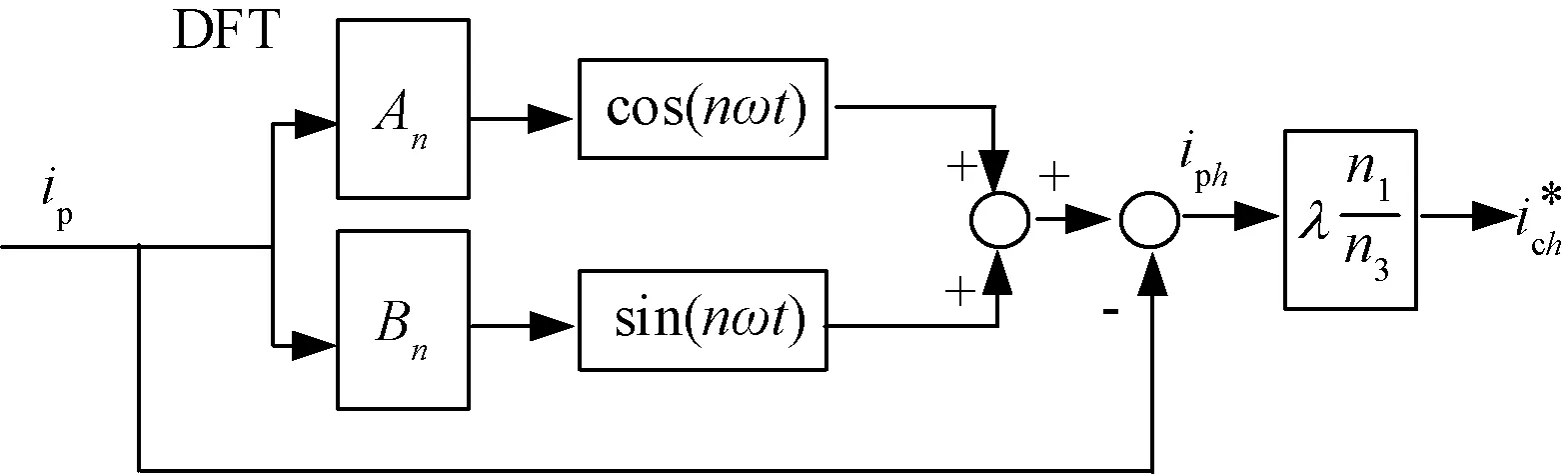
图7 滑窗离散傅里叶分析框图

与传统的离散傅里叶分析相比，滑窗傅里叶分析的方法减小了计算量。在数据更新时将N次求和计算减小为两次加减运算，提高了检测速度。且该方法检测精度高，提取的谐波电流指令准确。

3.3 影响补偿效果因素分析

由式( 3 )分析可知，为了完全补偿谐波电流使iph=0，补偿电流应为

(22)

此时为了产生补偿电流指令值，需检测到牵引绕组谐波电流之和ish。由于实际运行过程中，牵引变流器多重化运行，牵引侧有多个绕组，精确检测到牵引绕组的电流之和较为困难，故本文采用检测原边电流的方法。原边绕组中的谐波电流与辅助绕组产生的补偿电流之间存在如下关系

(23)

式中：λ为补偿系数。将式(23)代入式( 3 )，能够分别得到原边电流iph及补偿电流ich与牵引绕组谐波电流ish的关系为

(24)

(25)

从式(24)、式(25)可以看出，当补偿系数λ→∞，原边谐波电流iph→0，ich能实现完全补偿。可参考1.2节中关于辅助绕组电流峰值分析以及实际应用中对谐波电流的抑制需求来适当选择补偿系数，达到降低原边谐波电流的目的。

辅助变流器的谐波抑制功能要求其对谐波指令有良好的跟踪性能。由图6可知，谐波电流的误差Ei为

(26)

电流控制器若采用响应速度较快的比例控制，则Gp(s)=K，PWM传递函数为一阶惯性环节，输入信号为正弦，所以有

(27)

(28)

(29)

式中：Ts为PWM环节的采样时间；B为谐波电流幅值。若忽略电阻值有

(30)

其中,K为比例控制器的比例系数。

将其展开

(31)

其系数采用留数法求解。

(32)

(33)

式中：b1、b2为一对共轭复数。

对于稳态系统，Re(pn)<1，所以当λ→∞，系统的误差信号为

e(t)=(b1+b2)cos(ωht)u(t)+

(b2-b1)jsin(ωht)u(t)=

(34)

式中：θ为误差信号的初相角。即该系统无法实现指令电流的无差跟踪，其误差与指令电流的幅值及模型参数有关。误差信号的幅值为

(35)

从式(32)、式(34)可知，误差幅值与补偿系数λ、谐波角频率ωh、辅助侧交流电感L3成正比，与比例系数K成反比。

考虑误差的存在，将误差代入式(23)，此时补偿电流的实际值为

( 36 )

将式(36)代入式(24)，原边谐波电流可以表示为

( 37 )

从式(37)可以看出，在牵引侧谐波电流源一定、变比一定的情况下，补偿系数λ越大，误差信号幅值|e|越小，则原边谐波电流越小，补偿效果越好。当谐波频率较低时，误差较小，λ的变化导致原边谐波电流呈倍数变化，补偿系数影响较大，原边谐波电流补偿后的幅值约为补偿前的1/(1+λ)；误差信号幅值|e|受谐波频率、交流电感、λ等取值的影响，λ越大，谐波频率越高，误差信号对原边谐波电流的影响越明显。

4 仿真及实验结果

以某型电力机车为研究对象，利用Matlab/Simulink进行仿真。首先对谐波抑制方案的可行性进行验证，观察该方案对辅助变流器直流侧输出电压及交流侧电流幅值的影响；通过仿真研究交流侧电感的取值、开关频率及补偿系数对抑制性能的影响。

4.1 谐波抑制方案及其影响的仿真验证

系统的框图如图1所示，牵引变流器开关频率为450 Hz，辅助变流器开关频率为20 kHz，均采用单极性调制。由式(16)得到电感取值为50 μH，补偿参数λ取值为2。变压器电压电流等参数见表1。

若辅助变流器无谐波抑制功能，原边电流频谱分析如图8所示。

图9为辅助变流器进行谐波抑制后原边电流的频谱。从图9可以看出，该功能能够对牵引变流器产生的低次及2倍开关频率附近的谐波进行抑制。原边电流THD由1.83%下降为0.67%。

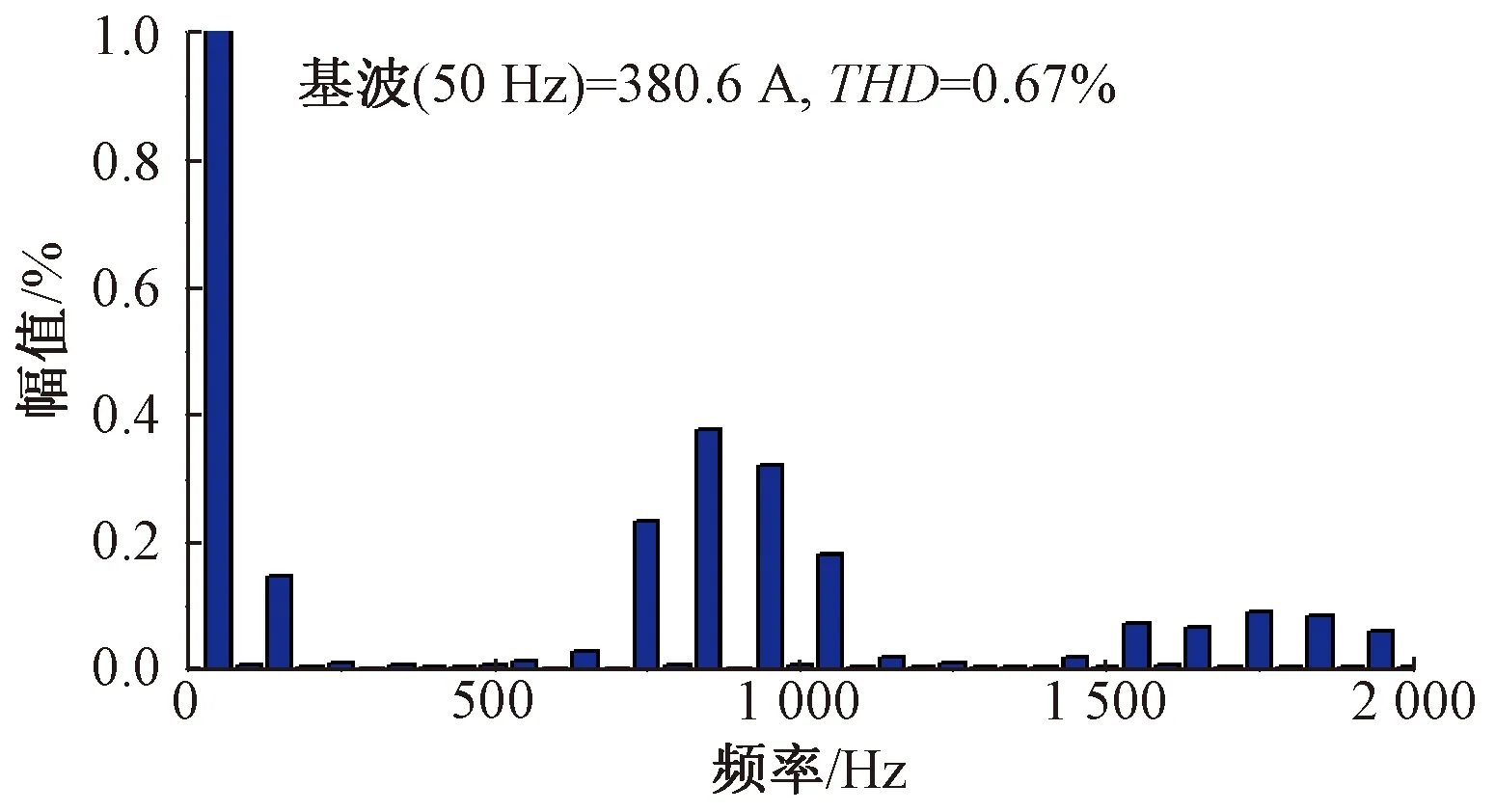
图9 补偿后原边电流频谱

图10所示为辅助变流器交流侧电流波形及直流电压波形。3 s时谐波抑制功能启动，从仿真结果可以看出，电流ic的幅值由1 000 A上升为1 200 A<(1 000+580)A (此时牵引变流器注入的谐波电流折算到辅助侧再乘补偿系数约为580 A)，满足式( 7 )对电流幅值的要求；直流侧电压在3 s前后始终保持在600 V左右，即该功能对辅助侧直流输出影响较小，不影响其对机车供电设备供电。

图10 辅助侧直流电压及交流电流波形

辅助变流器谐波抑制方法对牵引侧产生的各次谐波有比较明显的抑制作用，在谐波频率变化时能够实时跟踪抑制，与指定次谐波抑制相比有更好的灵活性；该方案对辅助侧直流电压影响较小，不影响辅助变流器为其他设备供电，但会导致交流侧电流幅值增大，对器件的耐压提出更高要求。

4.2 参数变化对抑制性能影响验证

由前述分析可知，影响辅助变流器谐波抑制性能的参数主要为辅助交流侧电感、开关频率及补偿参数的取值。

4.2.1 交流侧电感、开关频率影响仿真研究

第2节对电感取值进行了详细分析，由式(15)、式(37)可知，开关频率通过影响电感取值及误差幅值，对谐波抑制性能产生影响。

图11比较了对于同样的指令电流，不同开关频率下的跟踪情况。从仿真结果可以看出，对于同样的谐波电流指令，开关频率越高，实际电流的跟踪性能越好，即产生的补偿电流能够更好地补偿牵引侧产生的谐波电流。

图12比较了对于同一开关频率，不同电感取值对电流跟踪性能的影响。从仿真结果可以看出，电感取值为50 μH时，实际电流与指令电流重合度较高，基本能跟踪指令电流；随着电感的增大，跟踪能力变差，谐波抑制能力被削弱。

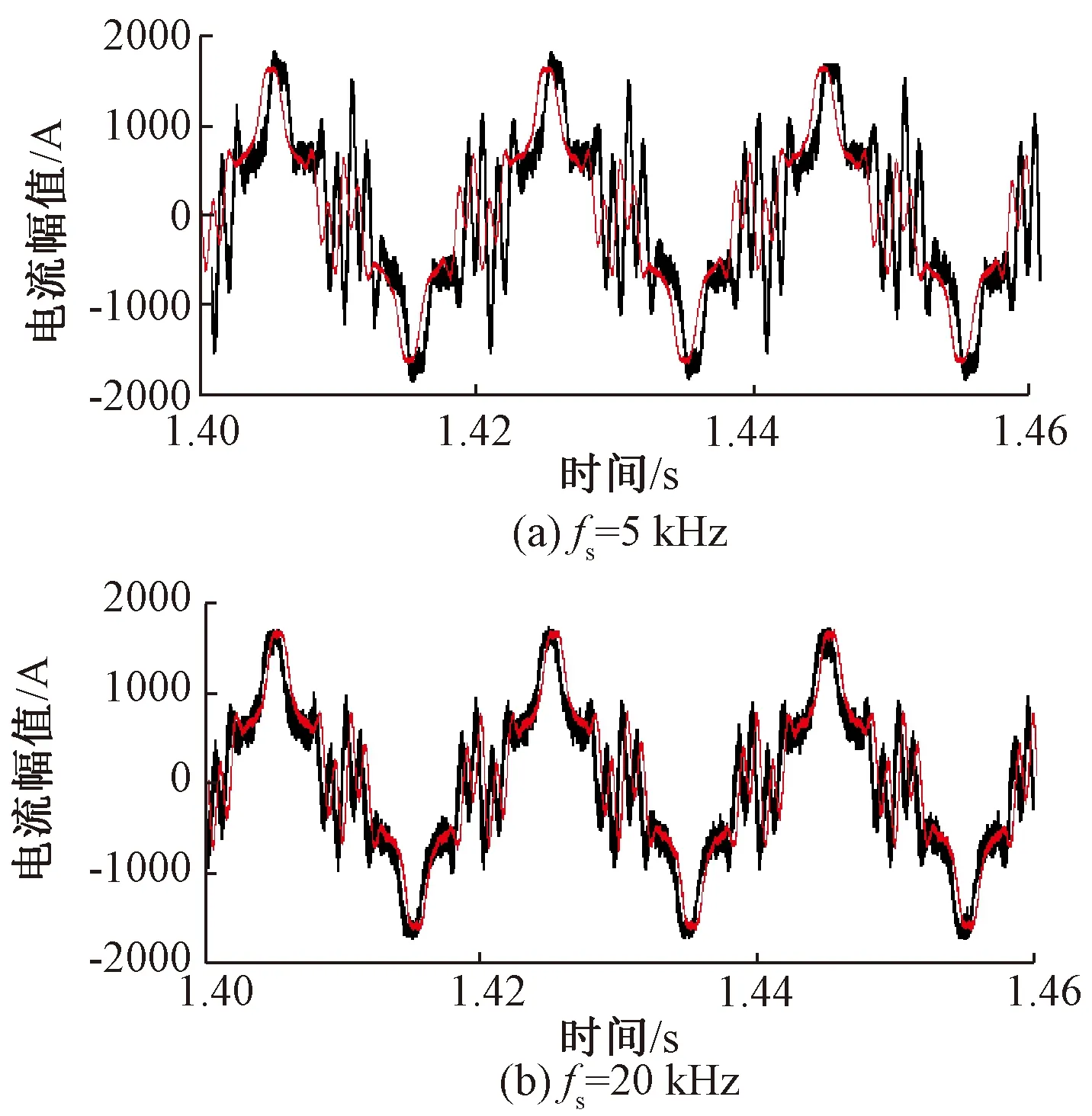
图11 不同开关频率下跟踪性能

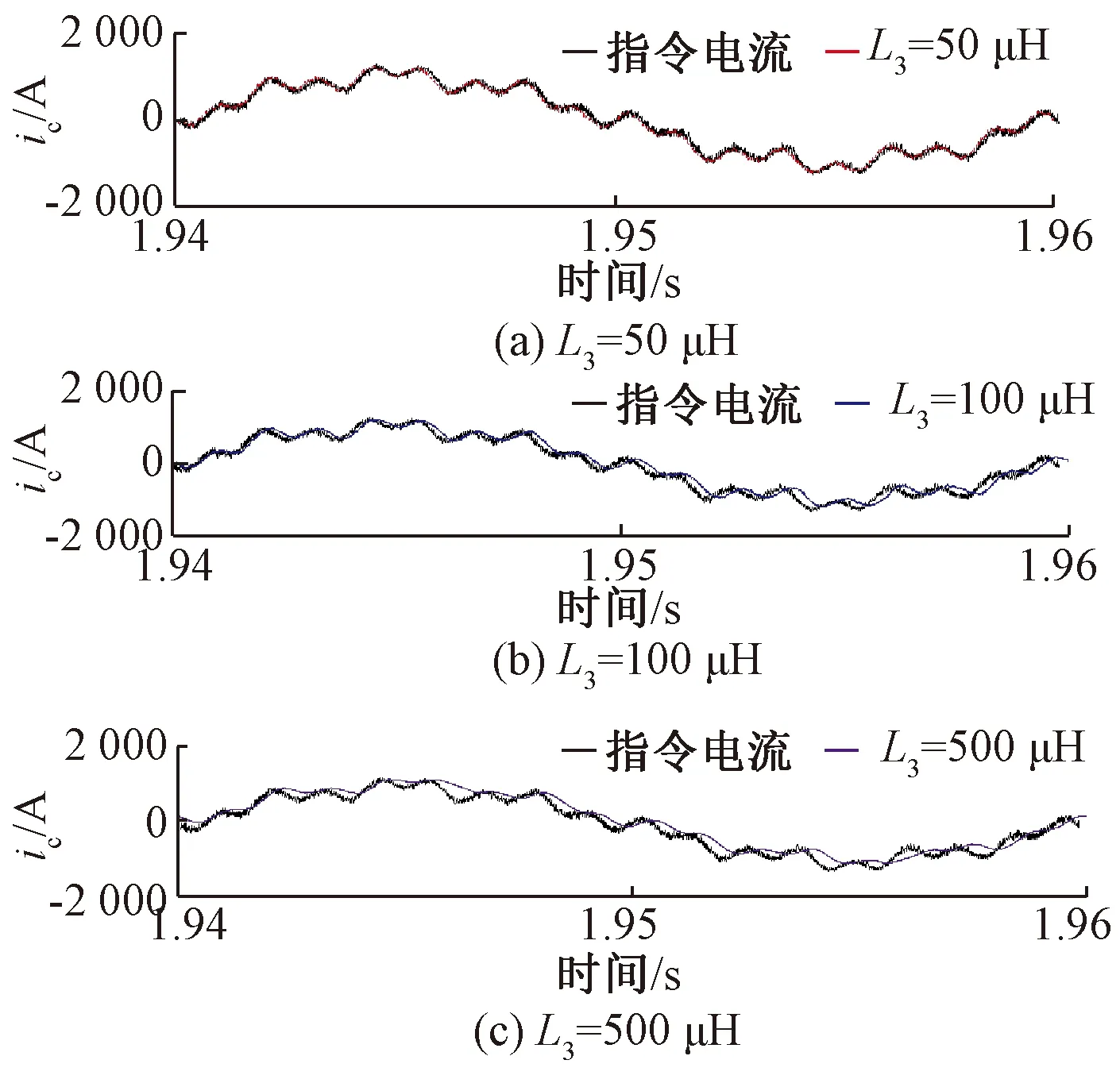
图12 电感取值不同的跟踪性能

图13给出了开关频率分别为5、20 kHz，谐波频率在850～2 550 Hz变化时原边谐波电流在抑制后的幅值。从图13可以看出，针对同一开关频率，随着横轴谐波频率增大，误差|e|增大，抑制效果变差；开关频率为20 kHz的抑制效果要优于5 kHz的抑制效果，验证了使用SiC器件高压高频特性的必要性。

图13 开关频率不同对抑制效果的影响

4.2.2 补偿系数对抑制效果影响仿真研究

由第3节分析可知，控制环中影响谐波抑制效果的参数为电流环的比例系数及补偿系数，从式(37)可以看出，λ对原边谐波电流影响较大。

牵引侧注入某些特定频率的谐波电流，定量观察该次谐波的变化以研究补偿系数λ变化对谐波抑制效果的影响。仿真中牵引网侧为幅值46 A、频率850 Hz的谐波电流源，电流环的比例系数K=1，基波电流幅值为386 A。辅助变流器开关频率设置为20 kHz。

将谐波电流注入后，变压器原边电流的傅里叶分析结果如图14所示，其中频率为850 Hz的谐波含有率为0.93%。

图14 补偿前原边电流傅里叶分析结果

辅助变流器的谐波抑制功能投入后，不同对的λ值对应的原边电流频谱如图15所示。

图15 λ取值不同原边电流傅里叶分析结果(fs=20 kHz)

从图15可以看出，λ=1时，频率为850 Hz的谐波电流含量变为原来的1/2，由0.93%降低为0.46%；λ取不同的值，对应的原边850 Hz谐波电流降低为原来的约1/(1+λ)，符合式(37)的规律。

通过仿真验证了辅助变流器谐波抑制方案的可行性，该方案能够补偿牵引变流器注入原边的谐波电流，且适用于多种频率，提高了牵引网的电能质量，能够避免谐振事故发生；增加的谐波抑制方案对辅助变流器为辅助设备供电的功能没有影响，但对器件耐流提出了更高要求；验证了开关频率、电感、补偿系数等参数变化对补偿性能的影响，与理论推导基本吻合。

4.3 实验结果分析

利用RT-LAB半实物平台进行实验以验证该控制算法的可行性。

4.3.1 RT-LAB半实物平台

图16所示为RT-LAB半实物实验平台的示意图，实验台主要分为三部分：上位机，OP5600仿真机及DSP+FPGA控制板。

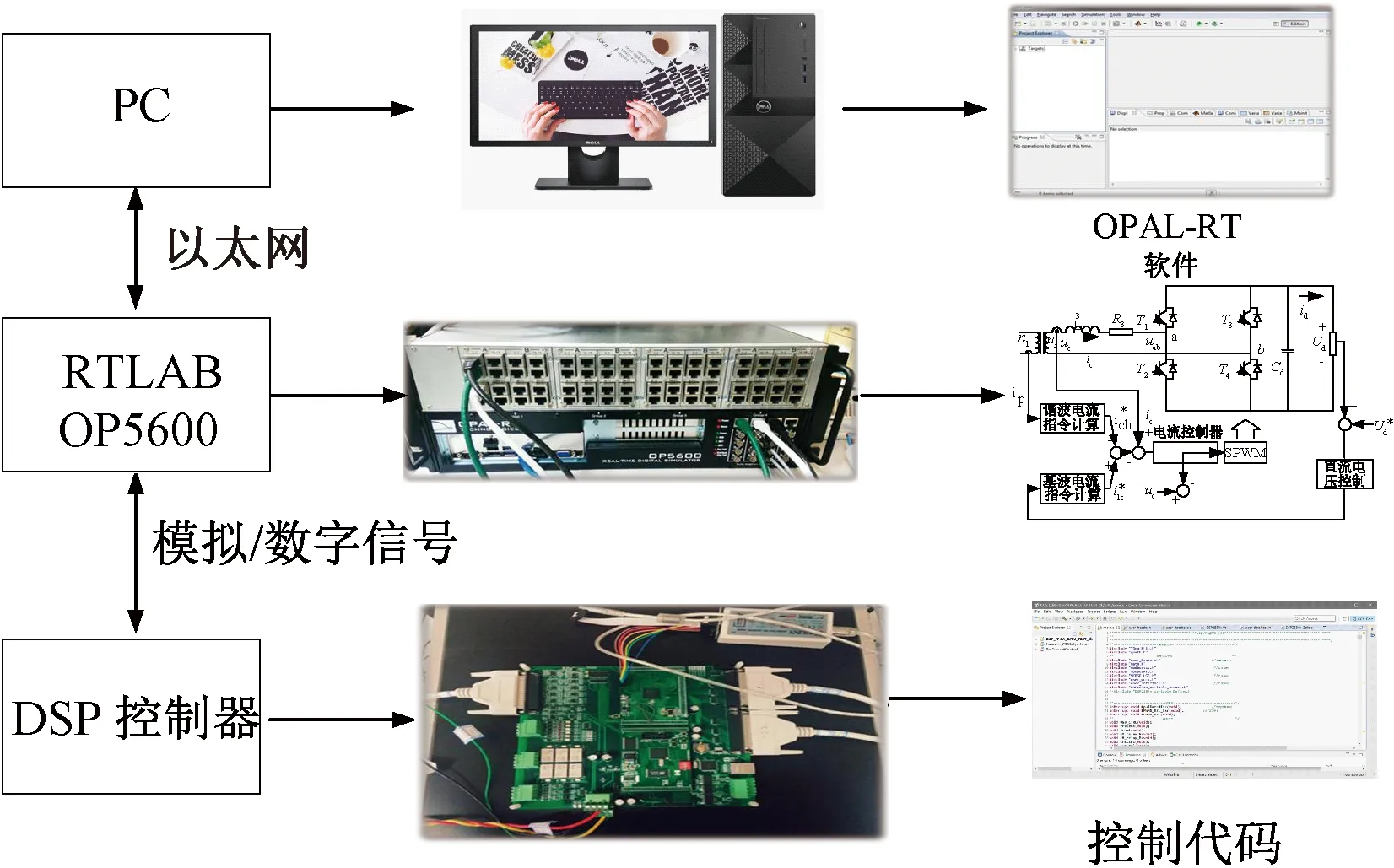
图16 RT-LAB示意图

实验中由于计算精度的限制，开关频率上限为5 kHz。实验中采用5 kHz的开关频率，对850 Hz的谐波电流进行抑制，从而验证控制方案的可行性及补偿参数变化对抑制效果的影响，同时验证该方案对变流器整流功能的影响。

4.3.2 谐波抑制方案实验结果

当牵引侧注入3.6 A、850 Hz的谐波电流，实验中原边基波电流幅值测量值为371 A，谐波抑制功能启动前原边电流的频谱如图17所示.

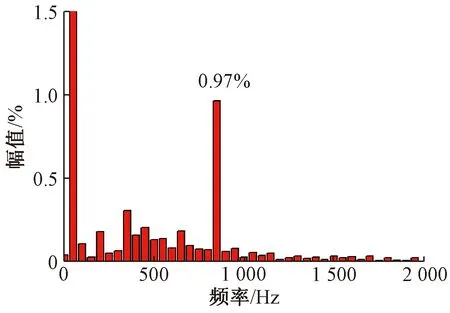
图17 RT-LAB频谱

辅助变流器谐波抑制功能启动后，当补偿系数λ取值不同时，原边电流频谱如图18所示。

图18 λ变化时原边电流频谱(fs=5 kHz)

通过分析实验结果可以得出，辅助变流器谐波抑制控制算法能够抑制牵引变流器产生的谐波，在算法投入后850 Hz谐波的含量下降。且当补偿系数变大时，对应次谐波电流下降率增大，λ越大，谐波抑制效果越理想。

图19为辅助变流器直流侧输出电压波形图，辅助侧四象限变流器仍能保持直流侧600 V的电压输出，为车载辅助设备供电。图20为辅助变流器交流侧电流波形，幅值由1 000 A增大到1 400 A，对器件耐流提出更高要求。

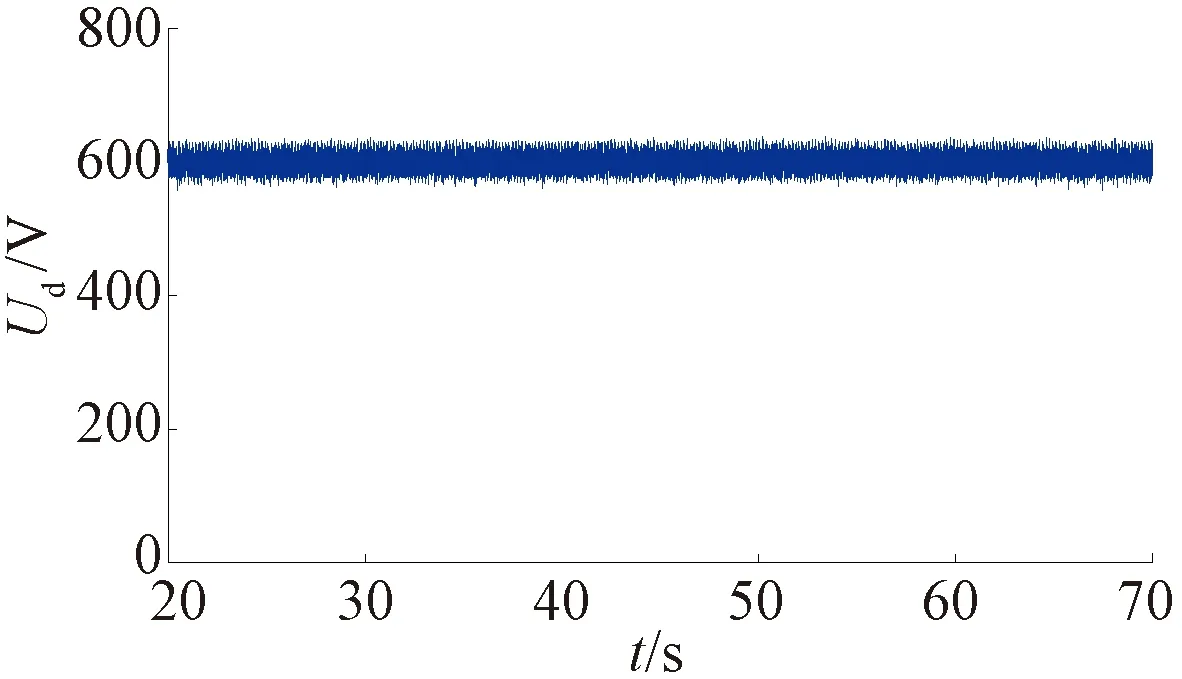
图19 辅助变流器直流侧输出电压

图20 辅助变流器交流侧电流

5 结束语

本文针对电力机车牵引变流器产生谐波、引发谐振事故、影响电能质量等问题，提出一种利用辅助变流器抑制牵引系统谐波的方案。

该方案适用于辅助电源从辅助绕组取电的电力机车。辅助变流器完成整流功能的同时，降低原边的谐波电流，不需要引入额外的硬件电路；对频率变化不敏感，能够实现各次谐波电流的动态跟踪补偿。

为完成谐波抑制功能且不影响辅助变流器为辅助设备供电，本文基于以上两种功能对辅助侧电感进行确定，其电感最小值与辅助变流器开关频率成反比，最大值与谐波频率存在定量关系。对电流环建模，理论推导确定了辅助侧补偿电流的公式及误差公式，其补偿能力与补偿系数λ及开关频率、电感值、谐波频率有关：补偿后谐波下降为原来的1/(1+λ)；对于850～2 550 Hz的中高频谐波，开关频率为20 kHz，电感取值范围为21～105 μH时，补偿效果较好。通过仿真及RT-LAB半实物实验对控制方案进行了验证。