基于Lamb波的CRTSⅡ型板式无砟轨道层间损伤检测方法

李再帏，吴 刚，朱文发，柴晓冬

(上海工程技术大学 城市轨道交通学院, 上海 201620)

CA砂浆层在CRTSⅡ型板式无砟轨道结构体系中将轨道板和支撑层黏结形成整体性较好的无砟道床。无砟轨道结构服役过程中，在轨道板温度梯度、列车动力荷载及基础不均匀沉降等因素耦合作用下，CA砂浆层普遍呈现了裂纹、离缝、掉块等结构性病害。CA砂浆产生损伤后，易形成轨道板板底脱空[1]。据相关资料统计[2]，2017年华东地区高温期(气温超过35 ℃)，高速铁路CA砂浆层离缝脱空病害显著，离缝大于2 mm的病害平均6处/km，见图1。

离缝脱空损伤会造成砂浆层与轨道板或支承层黏结失效，削弱无砟道床的整体性，影响轨道静态几何形位和动态稳定性。此外，在列车动荷载和环境因素综合作用下还会对其服役耐久性产生一定影响。已有研究[3]主要是关于砂浆层损伤对轨道、车辆的动力学和运营影响，但对砂浆的层间损伤信息进行定量检测是进行其他研究的重要前提条件，故对CA砂浆层离缝脱空损伤检测方法展开深入研究有十分重要的理论价值和实践意义。

针对CA砂浆层离缝脱空损伤的检测问题，国内外学者进行了一定量的研究，主要可以分为模态分析法、弹性回波法、声波诊断法等。文献[4]对轨道板-CA砂浆层有限元模型进行曲率模态分析，利用系统的一阶曲率模态对CA砂浆层间损伤进行识别。文献[5]通过构建轨道板-CA砂浆层-支撑层的三维有限元模型，研究了弹性波在其模型中传播特性，采用力锤回波实验验证了理论分析的正确性，并通过预制CA砂浆缺陷实验说明了弹性回波法在检测CA砂浆层间损伤的有效性；文献[6]采用相类似的原理，通过计算轨道板的导纳来确定CA砂浆层损伤。文献[7]则在传统弹性回波法基础上，采用检波器阵列式的方式进行CA砂浆层损伤检测。此外，文献[8]采用与德国高铁相类似的声传感技术，通过在线路典型路段布设声传感器，收集高速列车通过轨道结构时的声信号，利用GBRT分类算法对CA砂浆层损伤进行识别。这些检测方法极大地解决了现场应用的需求，为保证无砟轨道安全可靠服役状态提供了技术支撑。但这些方法多是只针对敏感区段进行定点检测，可移动性较差，且多采用接触式方式进行检测，效率极低。因此，需要一种移动性强且为非接触式的CA砂浆损伤快速动态检测方法。

基于此，本文提出采用空气耦合超声Lamb波对CA砂浆离缝脱空损伤进行检测。Lamb波是超声在板状结构中传播的一种应力波，其沿板横向传播过程中，对板内及层间缺陷损伤等具有较强的敏感性，具有非接触、检测速率高、在线扫描及原位检测等优点[9-10]，特别适合于板式无砟轨道这样的多层板构造物的损伤在役检测。文献[11]研究混凝土板中Lamb波的传播特性。文献[12]基于空气耦合超声无损检测非接触、无损伤的检测特点，总结了其发展历程以及提高检测效率的两种方法。文献[13]基于Lamb波检测模式，从理论计算和实验分析上对钢板中空气耦合超声波透射率与入射角的关系并进行了比较。在此基础上对不同开口裂纹的钢板进行损伤成像，并用有限积分法验证了实验结果的一致性。文献[14]利用Lamb波分别对转向架的完好结构、检测结构相应导波能量谱同激励信号的相关系数进行计算分析，得到检测结构的损伤指数并加权得到损伤概率密度大小，从而实现转向架损伤的定位诊断成像。文献[15]通过构造基于Lamb波散射的过完备块稀疏字典，采用谱梯度投影法求解加权块稀疏凸优化模型，将得到的损伤散射信号稀疏表示系数作为损伤指标，实现对被测结构的损伤成像。

本文通过建立CRTSⅡ型板式无砟轨道Lamb波传播理论模型，研究无砟轨道中Lamb波的频散特性，确立对缺陷敏感的Lamb波模态以及在空气耦合方式下该模态的激励参数。通过在实验室内进行无砟轨道板的1∶1比例模型实验，验证本文所提Lamb波检测CA砂浆层离缝脱空损伤的有效性和准确性。

1 Lamb波在无砟轨道中传播的理论模型

CRTSⅡ型板式无砟轨道是典型的层状板结构，其厚度方向尺寸远小于其在线路纵向长度和横向宽度方向的尺寸，因此可将轨道板状结构中声传播问题作为平面应变问题。空气耦合超声波通过空气以一定角度斜入射至轨道板上表面，在轨道板上下界面反射传播一定距离后不断发生波形转换而形成板结构中面正对称和反对称的各模态超声Lamb波。超声波是一种机械波，由于质点振动具有一定的机械能，故波的传播过程也即是能量的传播过程。建立CRTSⅡ型无砟轨道板刚性边界条件下空气耦合超声Lamb波声传播能量泄漏模型，见图2。

图2 CRTSⅡ型板刚性边界条件下Lamb波声传播模型

图2中，θ为空气中斜平面波的入射角度；ρa、ca分别为空气的密度、声速；λ、μ为轨道板材料弹性常数；ρ为密度，kg/m3。激励和接收探头相距L，同位于轨道板上侧，且倾斜θ角度相向对称布置以便激发和接收特定模态Lamb波信号。CRTSⅡ型板式无砟轨道主要材料特性见表1。

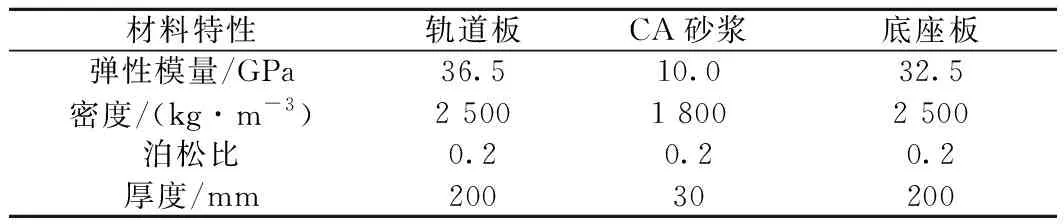
表1 CRTSⅡ型板式无砟轨道主要材料特性

基于能量角度考虑，当Lamb波在板状结构中向前传播时，能量不断向轨道板下侧泄漏，能量的泄漏是通过轨道板与CA砂浆之间刚性界面发生的，能量泄漏大小与该刚性界面大小有关[16]。设CA砂浆层间存在脱空损伤，且其在水平面上位于Lamb波传播路径上，当激励和接收探头之间距离L一定时，则两探头之间刚性界面越大(即脱空损伤面积越小)，能量泄漏越多，接收探头能接收到的信号能量越少，幅值越低；反之，若刚性界面越小(即脱空损伤面积越大)，则能量向下泄漏越少，接收探头能接收到的信号能量越多，幅值越高。故由接收到的Lamb波信号能量幅值能表征CA砂浆损伤的情况，可以实现对CRTSⅡ型板式无砟轨道层间损伤的定量检测。

2 轨道板频散特性与空气耦合激励参数选择

2.1 频散特性

Lamb波的传播特性十分复杂，主要表现为频散特性和多模态现象，即速度随频率变化而变化，以及同一频率下对应至少两种Lamb波模态。为激发具有较高敏感性的特定Lamb波模态，实现对CA砂浆层间脱空损伤的快速检测，需要进行轨道板中Lamb波理论频散曲线求解和传播特性分析。由文献[16]可知，对CRTSⅡ型板式无砟轨道的多层结构，当检测CA砂浆层间脱空损伤问题时仅需计算轨道板单层频散，从而确定探头激励参数。

如图2所示的轨道板层，无外力作用下板状结构动力学控制方程为

(1)

式中：u为位移矢量，m。

由Helmholtz分解原理可知，将轨道板中的位移场表示为标量势的梯度和零散度矢量的旋度，得到2个分离的波动方程，对平面应变问题有

(2)

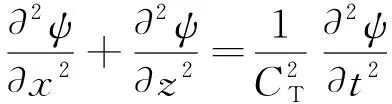
(3)

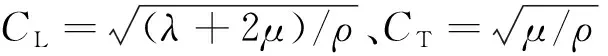
由平面应变假设，位移和应力通过势函数φ和ψ分别表示为

φ=Φ(z)exp[j(kxx-ωt)]

(4)

ψ=Ψ(z)exp[j(kxx-ωt)]

(5)

式中：Φ和Ψ为对应势函数幅值；z为z轴方向；j为虚数单位；ω为角频率；kx为沿x方向波数，由Snell定律可知kx=kasinθ，1/mm。其中，ka为波数。

将式(4)和式(5)分别代入式(2)和式(3)，可得

Φ(z)=A1sin(pz)+A2cos(pz)

(6)

Ψ(z)=B1sin(qz)+B2cos(qz)

(7)

轨道板中位移和应力可由含有以z为变量的正弦(或余弦)函数的势函数表示，而正弦(或余弦)函数是关于z=0的奇(或偶)函数，故可把解分为正对称和反对称模态，经适当变换，通过应用零应力边界，可确定Lamb波传播的频散方程为

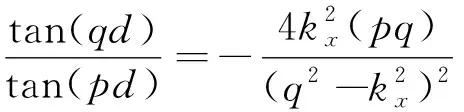
(8)

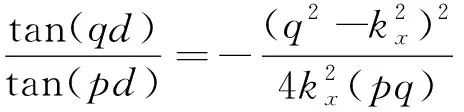
(9)

式中：d为轨道板的厚度。

式(8)和式(9)即为Rayleigh-Lamb频散方程，且为含两个参变量的超越方程，很难求取解析解。利用Matlab软件编程得到200 mm厚单层轨道板频散模型，轨道板厚度一定，采用二分法对上述频散曲线方程进行迭代数值求解，得到频散方程每对应频率下的有限个实根，即轨道板相速度cp与频率的频散关系。为获得特定频率下模态激励角度和验证所激励模态准确性，同时还需求得各模态群速度cg、入射角θ同频率的关系分别为

(10)

θ=arcsin(ca/cp)

(11)

式中：k=ω/c。

基于以上计算方法得到轨道板Lamb波相速度、群速度、入射角分别随频率变化的相关频散曲线见图3。图3中，CR为Rayleigh波速，A0、A1、A2、A3为Lamb反对称模态，S0、S1、S2、S3为Lamb对称模态。

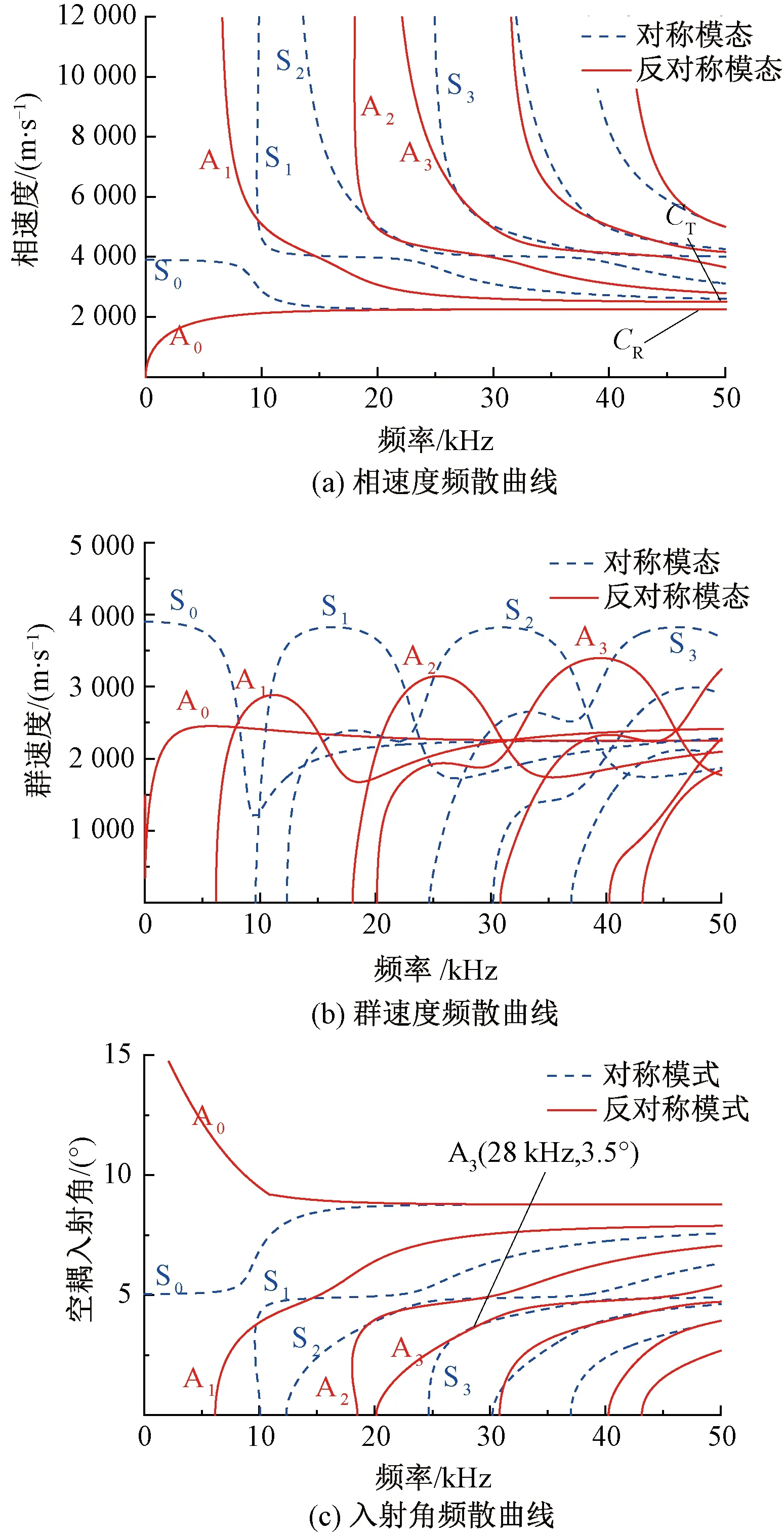
图3 轨道板中Lamb波频散曲线

由图3可知，曲线的非线性体现了其频散特性，除A0和S0外，每个Lamb波模态都存在有截止频率，即每个模态都有其存在和传播的频率范围，模态阶次越高，截止频率也越大，且每个频率对应至少两种以上模态，频率越高，对应模态数越多。

2.2 空气耦合超声Lamb波激励参数选择

通过空气耦合方式激发在轨道板中超声Lamb波时，空气和轨道板声阻抗相差较大(常温常压条件下，空气声阻抗：Za=428.6 Rayl、轨道板声阻抗：Zs≈107Rayl)。为增大入射声波的穿透性，要求入射波波长较长，即频率较低，较长波长能减少混凝土粗骨料和钢筋对接收信号的不利影响[17]。由轨道板的频散曲线可知，声波激励频率越高，衰减越快；频率越低，干扰的Lamb波模态数越少，但频率太低也会带来频散严重的问题。

由于频散、多模态的存在及各模态对板层间损伤敏感性不一致的特性，使得在实际线路轨道检测时接收信号复杂，难于进行模态识别和分析处理。因此，需要激发对轨道板CA砂浆层间损伤较敏感的单一Lamb波模态来检测，以避免其他模态的存在而产生模态混迭等问题。一般而言，对于薄板或半无限大结构亚表面的埋藏缺陷多采用低频段的A0、S0模态来进行检测[9]；而对于无砟轨道板CA砂浆层间脱空损伤，随着频率增大，A0和S0模态收敛退化成表面波，速度收敛于表面波速CR，其他模态则退化为剪切波，波速收敛于剪切波波速CT，即Lamb波模态敏感性较低；因此，本文综合理论分析和文献[18-19]的研究结果，将A3模态确定为Lamb波的主要识别模态。

其次是建立机构，完善风险评估制度。可以建立相关风险管理机构，在校长领导下开展工作，由相关职能处室负责人和具备专业风险管理知识的人才以及一定经验的教师为主要成员，对学校重大事件进行风险评估。下设风险评估小组，对管理中的重大问题列出的风险清单，分析不同环节的关键控制点，制定相应控制措施或应对策略；为完善风险评估制度，风险评估小组还可以针对不同业务，给出风险评定标准，对涉及的风险点、风险等级进行评定，用以判断风险程度的大小。

为进一步确定适用的单一检测模态，在28 kHz频率下，200 mm厚轨道板中前四阶Lamb波反对称模态的波结构如图4所示；可知各模态沿轨道板厚度方向，面内位移成反对称分布，离面位移成对称分布，并且在板厚度的中间位置，面内位移为0，故离面位移越大越易于激发单一反对称Lamb波模态；A0、A3模态在轨道板表面具有较大的离面位移，即具有更为明显垂直于轨道板上下表面的振动位移，更适合于空气耦合超声探头激励和接收信号。但是，由轨道板频散曲线计算结果可知，28 kHz中心激励频率下，A0模态已同S0模态收敛退化为表面波，其声波能量集中并主要沿轨道板上表面进行传播，对轨道板板底脱空等损伤无检测能力而不适合用来进行检测，故选择A3模态用于进行CA砂浆层间损伤的检测。

图4 28 kHz下200 mm厚轨道板中Lamb波反对称模态波结构

此外，由表1中参数的轨道板频散模型计算得A0—A3模态群速度分别为2 260、2 160、2 970、1 893 m/s。在同频率和同能量密度的条件下，A3模态波速小，相应波长更小，对小尺寸损伤具有更好的识别检测精度。综上所述，本文选择A3模态进行激励检测。由图3(c)所示的入射角频散曲线可知，28 kHz时轨道板中A3模态理论空气耦合入射角为3.5°；考虑到空气耦合平面波探头所激发的超声波声束具有一定扩散角度，实际检测实验中，激励和接收探头相对轨道板上表面倾斜角为(3.5±0.5)°。

3 实验研究

3.1 实验试样

在实验室按照CRTSⅡ型无砟轨道尺寸进行1∶1比例制作试件，各层材料配比及用料严格按照TB 10005—2010《铁路混凝土结构耐久性设计规范》[20]和TB/T 3399—2015《CRTSⅡ型板式无砟轨道混凝土轨道板》[21]规定进行制作，水泥为金山牌P.O52.5水泥。

由现场调研结果可知[2]，CA砂浆层局部损伤在不断劣化情况下，损伤能逐步叠加形成贯穿性脱连等离缝脱空病害，为研究界面脱黏尺寸与Lamb波能量的关系，铺设前在CA砂浆层预先埋置200 mm×200 mm、400 mm×400 mm、600 mm×600 mm三种不同尺寸的贯穿脱空缺陷，以模拟CA砂浆层不同损伤程度工况。三种脱空缺陷的平面中心沿纵向CRTSⅡ型轨道板中心线平行等间距布置，且前后两端缺陷边缘至轨道板两端的距离同相邻缺陷之间的间距相等，三种脱空缺陷高度均为30 mm且贯穿砂浆层。制作好的混凝土无砟轨道结构试件进行标准养护，CA砂浆层除预置脱空损伤处与轨道板下界面脱黏外，其余地方均黏结完好。

3.2 实验系统搭建

实验搭建了无砟轨道空气耦合超声Lamb波无损检测系统，见图5。该检测系统硬件包括：28 kHz空气耦合超声激励和接收探头、多自由度旋转平移扫描架、高功率超声波激励接收仪(日本JPR-Probe公司生产，型号JPR-10CN，其可连续发射300个波数的矩形脉冲和增幅60 dB的高信噪比带通滤波信号内置增幅器)、后置信号放大器、示波器、计算机。软件为基于Matlab平台自主开发的信号处理和检测平台平移控制程序，实现整个检测系统的整合，控制空气耦合超声激励接收探头的入射角和水平距离。

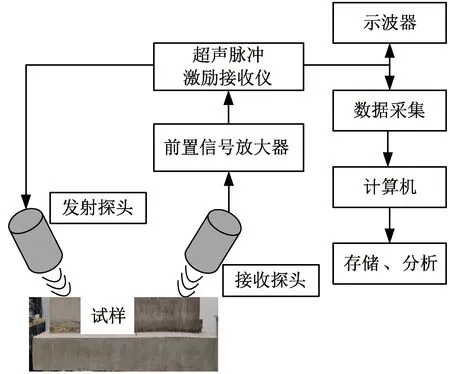
图5 空气耦合超声无损检测系统实验流程

计算机通过软件控制高功率超声波激励接收仪产生激励信号，经D/A转换为电信号，将电压施加在空气耦合超声激发探头的压电晶片激励器上激发超声波。空气耦合超声接收探头接收从轨道板泄漏至空气中的携带有CA砂浆层间脱空损伤信息的漏Lamb波信号，并经后置信号放大器进行放大后由A/D采集卡将模拟信号转换为数字信号，用于示波器实时显示和在计算机上显示、分析、记录、存储。

3.3 实验结果分析

调整激励和接收探头沿轨道板宽度方向分别位于不同缺陷平面位置的两侧，两探头连线中心点分别与预埋的不同尺寸脱空缺陷中心点重合(即激发、接收探头内侧分别到三种脱空缺陷边缘的水平距离相等)。两探头位于轨道板表面上方 20 mm 处，探头净间距L=650 mm，并在脱空缺陷中心点相向对称倾斜布置。

保持激发、接收探头间距和倾斜角度不变，依次同时移动激发和接收探头至各脱空缺陷上方，且激发和接收探头连线与各脱空缺陷中心线重合。实验采样率1 MHz，为消除信号采样误差及提高信噪比进行32次采样平均，调整探头入射角约为3.5°激发接收A3模态Lamb波。实验结果见图6。

图6 实验结果

由图6可知，实验接收信号首波群速度约为1 920 m/s，这与理论计算群速度1 893 m/s相近，故所接收信号首波为所激发A3模态，且其在时域上主要位于605～935 μs之间；空气声速约340 m/s，传播速度慢，由于无法完全隔断激发探头产生的声波而由空气直达接收探头，故1 400 μs后的信号波包基本为空气中直达的噪声干扰信号；当Lamb波遇到损伤时产生了模态转换，在935～1 400 μs之间出现了其他模态信号，使Lamb波频散现象变得严重，波包变得更宽；对比不同长度的CA砂浆层间脱空损伤可知，探头距离一定时，轨道板与CA砂浆层间的脱空长度越小，轨道板中Lamb波能量向下各层泄漏越多，直接导致接收到的Lamb波信号能量越少，幅值越低。进一步地对实验条件下接收Lamb波信号幅值与CA砂浆层间脱空损伤尺寸进行回归分析，见图7。由图7可知，损伤的尺寸与幅值呈现线性回归关系，可以通过信号的幅值近似地定量化评价CA砂浆层间脱空损伤程度。

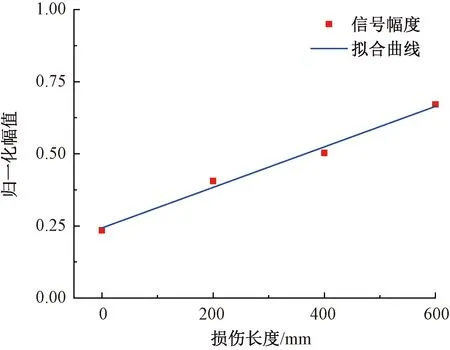
图7 归一化Lamb波幅值与损伤尺寸关系

综上实验结果，本文利用空气耦合超声Lamb波方法，可快速、有效地实现对CRTSⅡ型板式无砟轨道CA砂浆层间脱空、离缝损伤存在与否及损伤尺寸大小的非接触检测评估。

4 结论

本文建立了Lamb波在CRTSⅡ型板式无砟轨道中传播的理论模型，研究了无砟轨道板频散特性与空气耦合超声Lamb波的激励参数，利用实验室模型验证了所提Lamb波检测CA砂浆层离缝脱空损伤方法的有效性和准确性，结论如下：

(1)采用非接触式空气耦合Lamb波可以快速实现CRTSⅡ型板式无砟轨道层间损伤的定量检测。

(2)激励CRTSⅡ型无砟轨道板Lamb波的空气耦合超声探头中心激励频率为28 kHz、入射角3.5°，可利用Lamb波的A3模态进行轨道板层间损伤检测。

(3)Lamb波的A3模态幅值随CA砂浆层间脱空损伤尺寸增加而增大，呈现线性变化规律。为检测无砟轨道层间损伤大小提供了一定的参考依据。需要注意的是由于损伤几何形状及大小具有多样性，如何对各损伤进行取向、平面形状及深度等的检测是未来的研究重点。