货物运输“公转铁”与铁路车流径路联合优化模型

刘 畅

(中国铁路经济规划研究院有限公司 运输研究所，北京 100038)

调整运输结构，实施货物运输“公转铁”是降低社会综合物流成本，打赢“蓝天保卫战”的重要举措，而高质量落实该举措面临着众多复杂的运输组织问题。货流由公路转移至铁路后，铁路网的货运OD分布将会发生变化。货运OD是制定铁路车流径路方案的重要输入数据，该变化可能会导致铁路最优车流径路方案发生变化。另一方面，由于铁路各区段均有明确的能力限制，当铁路车流径路方案变化后又将会影响相关OD间的输送能力，进而影响相应的OD所能允许的铁路货运增量的限额。可见，公铁货流转移与铁路车流径路调整是紧密相关、互相影响的。此外，部分与繁忙公路干线平行的铁路也比较繁忙，没有充足的能力来承接公路转移来的货流。该情形下则需要将经由该铁路的部分车流调整至次短路以腾出该线路的能力来承接公路货流。将车流调整至次短路将会产生额外的绕行成本，该成本会与“公转铁”产生的效益部分相抵。“公转铁”的量越大，需要调整径路的车流可能就越多，产生的额外成本或许就越大，从而出现“效益背反”的现象。因此，为实现公铁两网整体综合物流成本的最小化，需要将公铁货流转移和铁路车流径路优化这两个问题统筹考虑。

另外，当某个OD间的公路货流转移至铁路形成车流后，该车流可能会有两种运输组织方式。当车流量达到开行始发直达列车的标准时，则开行点对点的始发直达列车，采用直达模式输送；当车流量未达到开行始发直达列车的标准时，需采用在编组站与其他车流组合成列，并在运输途中进行若干次有调中转的中转模式输送。上述两种车流组织方式有明显差别，其车流径路规划方法也有所不同。在直达模式下，车流径路规划一般需满足单股货流不可拆分约束。中转模式下的车流径路规划则相对复杂，由于编组站有调中转作业的特殊要求，当起点不同而终点相同的若干车流在某编组站汇合后，这些车流将被合并为一股车流，不再拆散。起点不同而终点相同的车流在输送过程中多次汇合，从而在宏观的视角下形成一棵树的形状，即“树形径路”规则[1]。可见，上述两种模式下的车流需要分别优化其径路。需要说明的是，由于我国的“公转铁”战略主要针对大宗物资，所以本文暂不考虑班列运输模式。

关于货物运输“公转铁”的理论研究起步较晚，成果相对较少。文献[2]通过权衡碳排放和运输时效性构建了公铁货流转移优化模型。在此基础上，文献[3]、文献[4]分别将公铁货流转移、铁路货运增量与铁路车流径路问题统筹考虑，构建了综合优化模型，但这些模型未考虑车流组织模式的差异，且模型次数较高，求解相对困难。文献[5]分析了“公转铁”政策的实施效果，针对政策实施过程中遇到的诸多问题提出了建设综合管理体系、加快推进基础设施衔接配套、营造良好发展环境等建议，但未就运输组织优化相关问题做深入探讨。铁路车流径路优化则是铁路运输研究领域的一个经典问题，成果非常丰富。文献[6-7]将多商品流理论应用于铁路车流径路优化，其中文献[6]通过改进决策变量使优化结果体现车流径路，文献[7]对两类车流径路优化模型做了细致的对比分析。文献[8-9]重构了考虑“树形径路”的铁路车流径路优化模型，实现了模型的线性化。文献[10]在车流径路优化问题中考虑了不同的车流组织模式，将车流分为直达车流、零散车流和快运车流三大类，并构建了考虑运输组织模式的车流径路优化模型。

上述成果为后续的研究提供了良好的理论参考。但是由于“公转铁”问题涉及公铁货流转移、车流组织模式变化以及不同类型车流的径路优化问题，而将这些问题统筹考虑的研究成果相对欠缺。本文构建了综合考虑上述因素的公铁货流转移与铁路车流径路联合优化模型，模型以公铁两网综合物流成本最小化为目标，通过权衡公铁货流转移的效益与铁路车流径路调整的成本，获得各OD间最优公铁货流转移量，同时根据货流转移后铁路发送量的大小判断其适用的车流径路规划方法，并就两种车流组织模式下的车流分别优化其径路。

2 模型构建

2.1 符号定义

模型相关符号见表1。

表1 符号及含义

2.2 目标函数

如前文所述，公铁货流转移的主要目的是降低全社会综合物流成本，因此在构建公铁货流转移优化模型时应将公路和铁路的综合物流成本均考虑在内，其中综合物流成本包括运输的货币成本、碳排放、事故率、噪声等。为便于分析计算，宜将上述指标的量纲都折算为货币单位。在考虑公转铁的情况下，公路运输的综合物流成本为

(1)

由于铁路货运量不同时可能会有不同的车流组织方案，所以当某OD间的公路货流转移到铁路后可能会有如下两种情况：

(1)公路货流转移到铁路后该OD间的货流量达到了开行始发直达列车的条件。那么由公路转移来的货流将与铁路原始货流一起编入始发直达列车。

(2)公路货流转移到铁路后该OD间仍不具备开行始发直达列车的条件。那么该OD间的货流将形成技术车流采用中转模式输送。

所以，考虑公铁货流转移及车流径路优化的铁路综合物流成本为

(2)

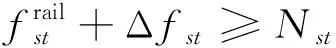
综上所述，旨在降低公铁货物运输综合物流成本的目标函数为

(3)

2.3 约束条件

(1)流量判断约束

为满足目标函数针对两种运输组织模式的货流分别求和的要求，引入辅助决策变量λst和μst并构造约束条件

(4)

(5)

(6)

(7)

(2)公铁货流转移量约束

由于转移货流是由公路转移至铁路，所以各OD的转移量应不大于公路原始的货运量。

(8)

(3)流量守恒约束

为保证各OD间铁路车流径路的完整性，需构造以下约束分别保证各技术车流径路和直达车流径路沿途所经由各点的流量守恒。

(9)

(10)

(4)“树形径路”约束

技术车流还应遵守“树形径路”规则。“树形径路”规则可等价地表述为：当终点相同的若干股货流在某支点汇合后，这些货流的下一个经由点必须选择同样的经由点[1]。基于该表述建立约束条件[9]为

(11)

(12)

式(11)和式(12)可解释为对于不同的起点s始发到同一终点t的货流，当其同时经由i点时，这些货流的下一个经由点只能选择同一个j点。

(5)绕行率约束

为保证货流“公转铁”的实施，部分铁路繁忙区段的车流需要适当绕行以腾出区段能力来承接公路的货流，但是车流的绕行率应在一定的限度内，因此在模型的求解过程中需要引入如下约束来限制车流的绕行率。

(13)

(14)

(6)线路能力约束

对于铁路网上的所有区段，流量的总负荷均不允许超过其能力限制，该能力约束为

∀(i,j)∈E

(15)

(7)节点装卸能力约束

由于各节点的装车和卸车能力有限，因此应当添加节点装车和卸车能力约束分别为

(16)

(17)

(8)变量取值范围约束

(18)

(19)

(20)

Δfst≥0 ∀s,t∈V

(21)

λst∈{0,1} ∀s,t∈V

(22)

μst∈{0,1} ∀s,t∈V

(23)

3 模型线性化处理及求解

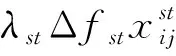
(1)第一次线性化

∀s,t∈V∀(i,j)∈E

(24)

∀s,t∈V∀(i,j)∈E

(25)

(2)第二次线性化

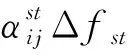
(26)

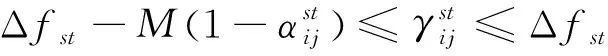
∀s,t∈V∀(i,j)∈E

(27)

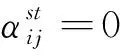
(28)

∀s,t∈V∀(i,j)∈E

(29)

至此，模型实现完全线性化。线性化后的完整模型为

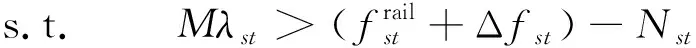
∀(i,j)∈E

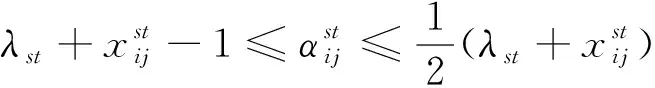
∀s,t∈V∀(i,j)∈E

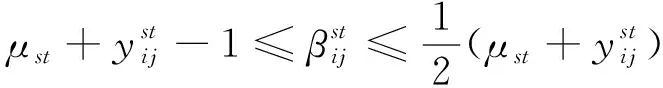
∀s,t∈V∀(i,j)∈E

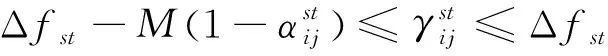
∀s,t∈V∀(i,j)∈E

∀s,t∈V∀(i,j)∈E

Δfst≥0 ∀s,t∈V

λst∈{0,1} ∀s,t∈V

μst∈{0,1} ∀s,t∈V

改进后的模型是一个混合整数线性规划模型，利用高效的商业求解器如Gurobi或Cplex等可快速求解。

4 算例分析

为验证模型的有效性，以下采用包含30个点的算例进行验证与分析。算例路网结构见图1。

图1 算例路网示意图

各区段里程及能力限制见表2。各节点的装卸能力见表3。各OD间原始公路运量、铁路运量及公路运输里程见表4～表6。由于400 km以下铁路相对公路运输几乎没有优势，货流很难从公路转移至铁路，因此在求解公铁转移问题时不考虑运距在400 km以下的公路货流。其他参数取值见表7。

将上述数据带入模型，采用高效商业求解器Gurobi进行求解。根据求解结果，共计5 065万t货物由公路转移至铁路，公铁两网总成本下降95.73亿元。其中有公铁转移发生的OD及其转移后的运输组织方式和车流径路等信息见表8。由于篇幅有限，此处仅列举转移量在20万t以上的OD。

从模型求解结果可以看出，通过求解该模型可以在统筹考虑铁路点线能力、运输组织模式以及车流径路优化等因素的条件下，获取使公铁两网综合运输成本最低的公铁货流转移方案，从而实现优化运输结构，降低社会综合物流成本的目的。同时，模型输出的公铁货流转移后铁路各OD间的车流组织模式及相应的径路也将为铁路运输组织提供参考。由此可见，该模型的求解结果达到预期，其可行性和有效性得到验证。

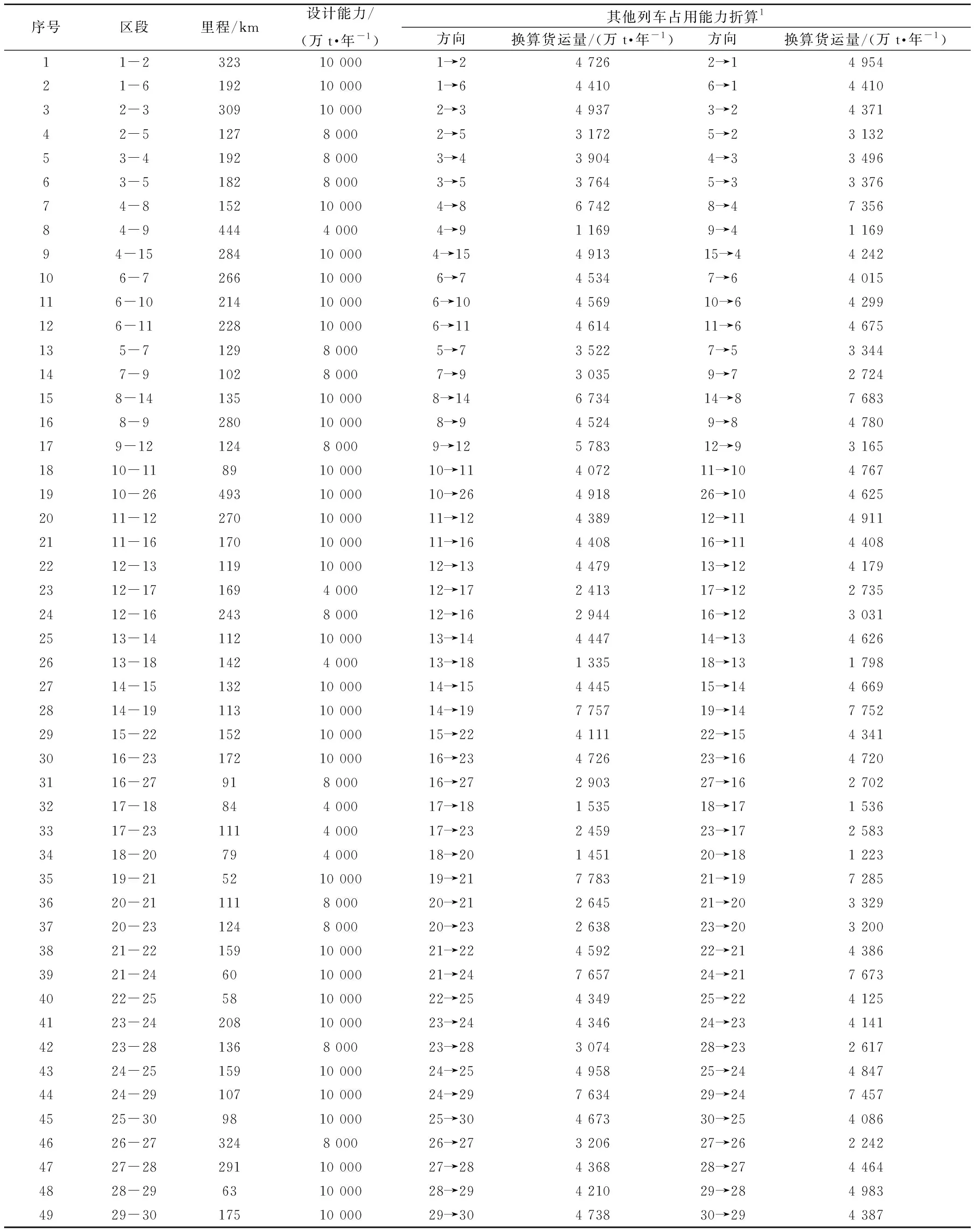
表2 算例路网各区段里程及能力限制

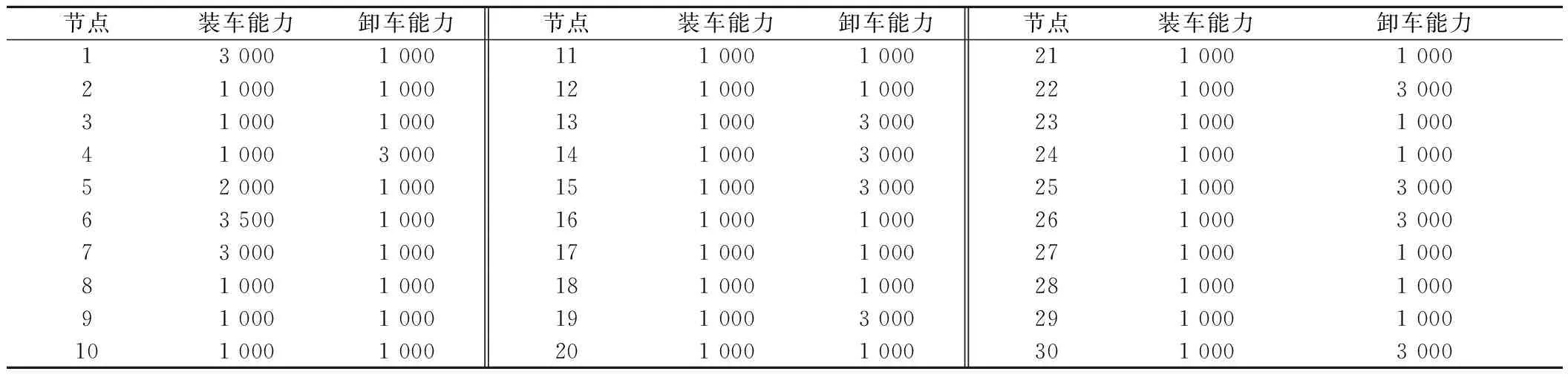
表3 各节点装卸能力 万t/年

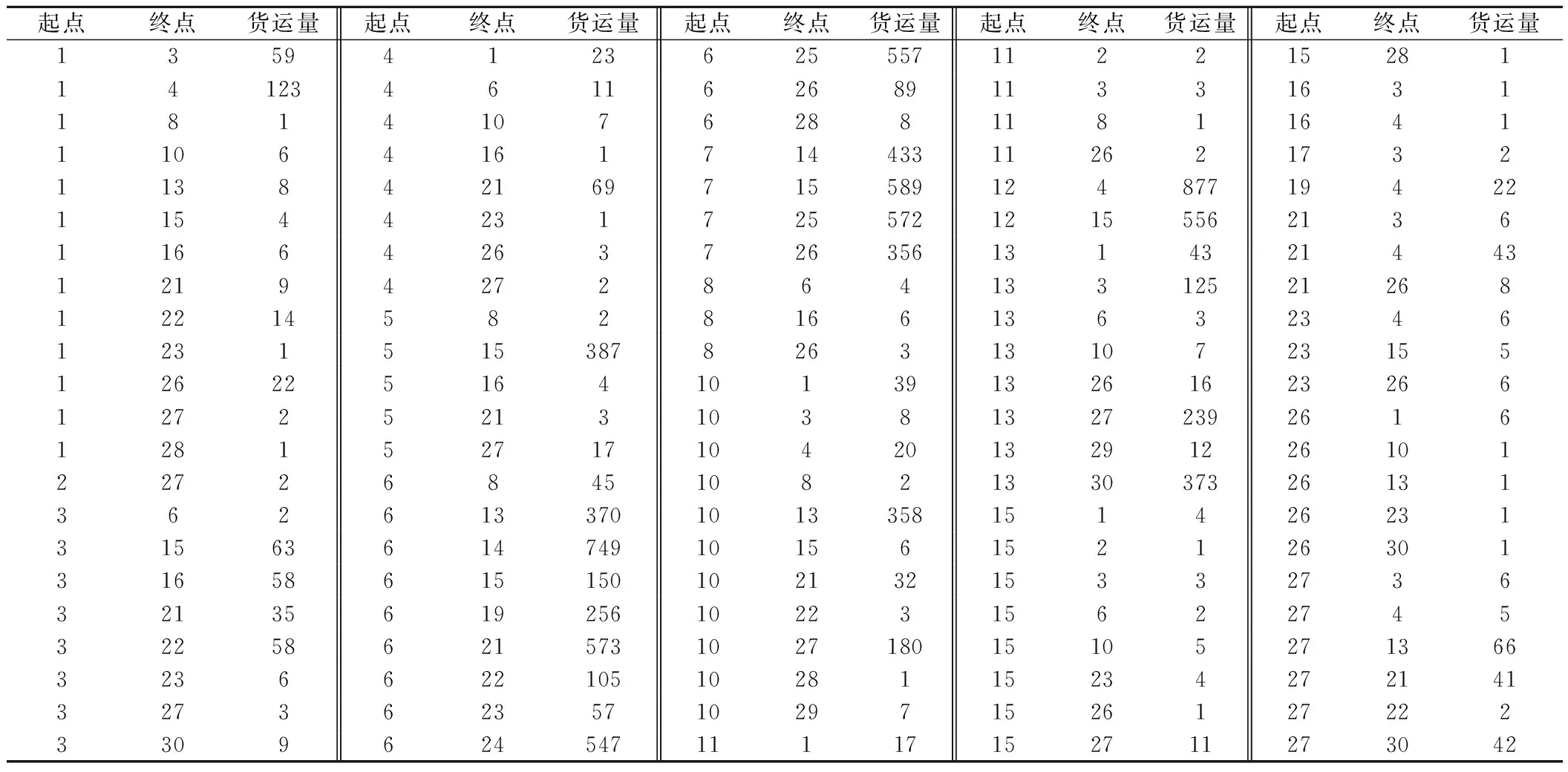
表4 公路原始货运OD 万t/年

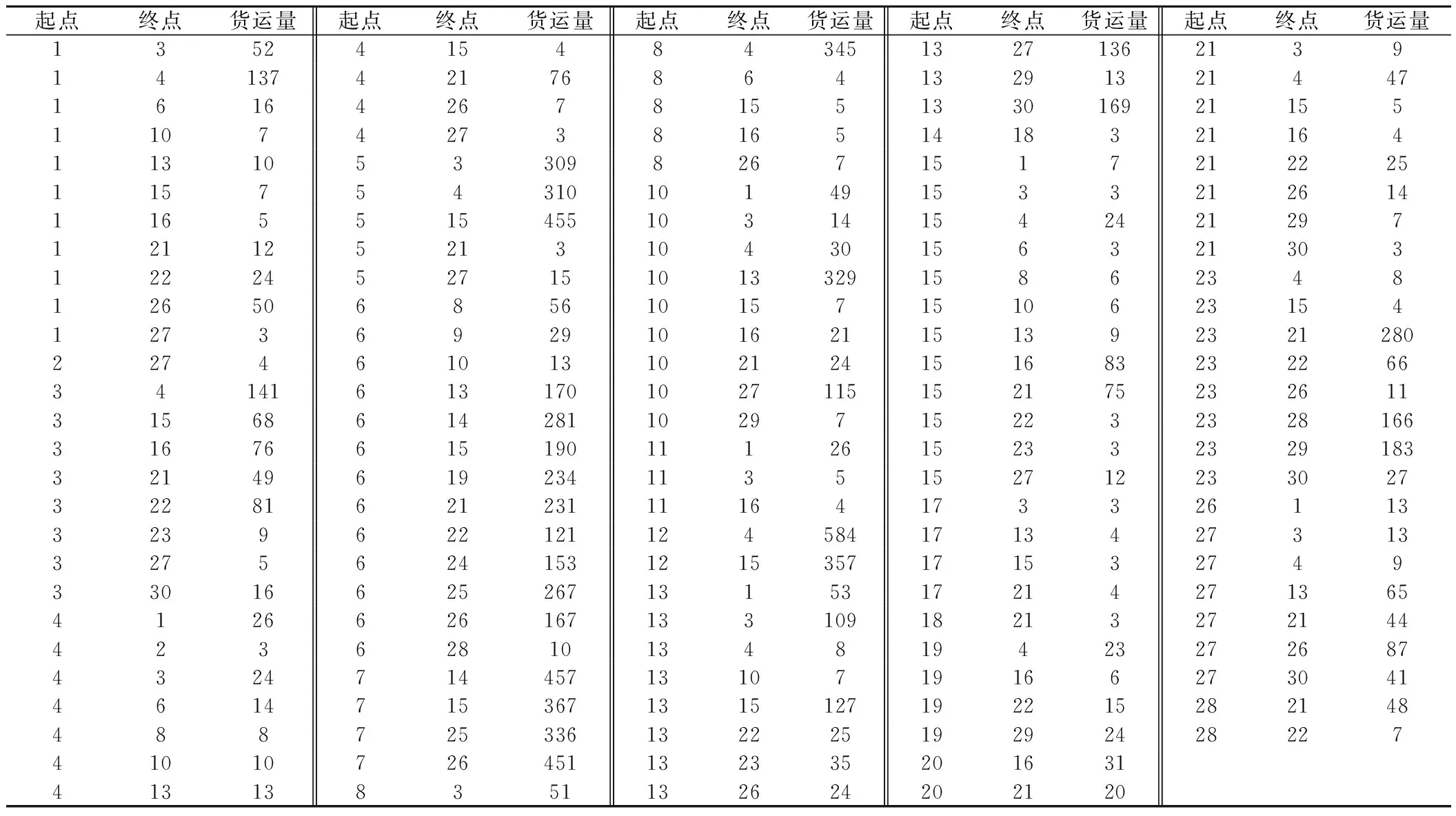
表5 铁路原始货运OD 万t/年

表6 各OD间公路运输里程 km

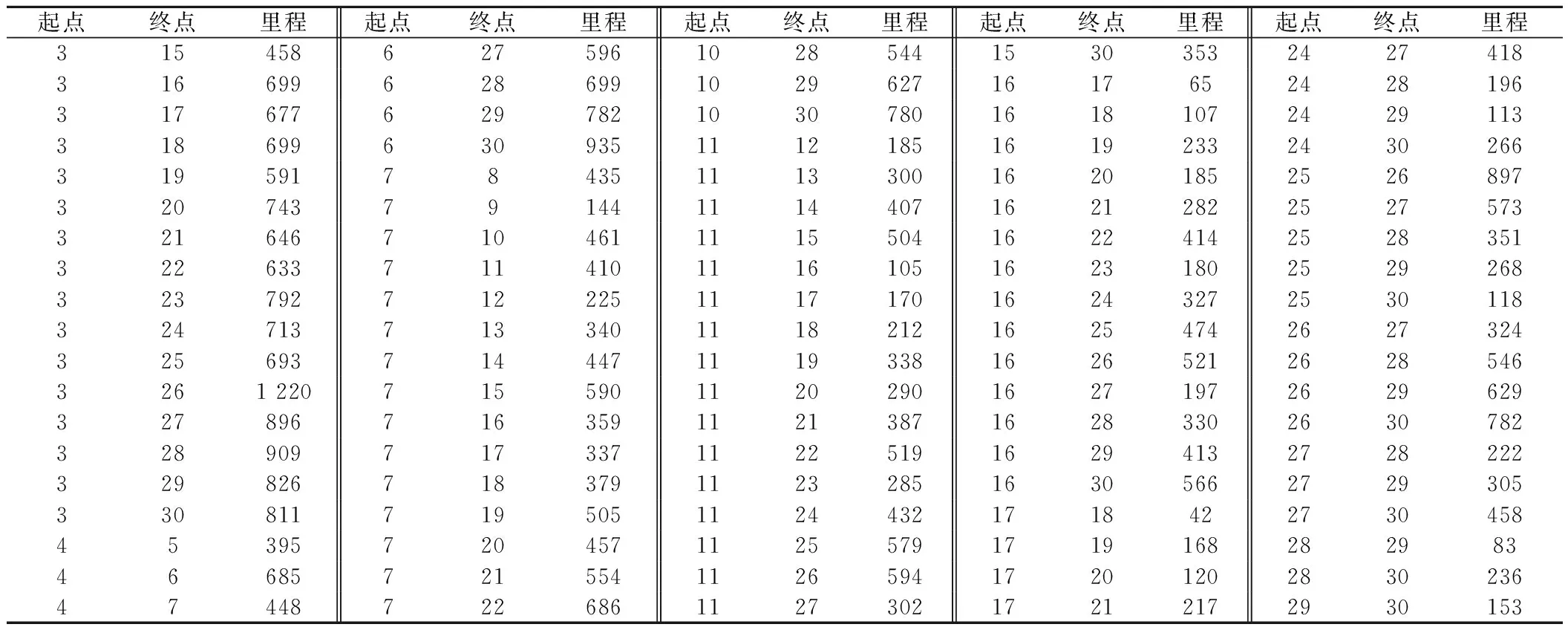
表6(续) km

表7 其他参数取值

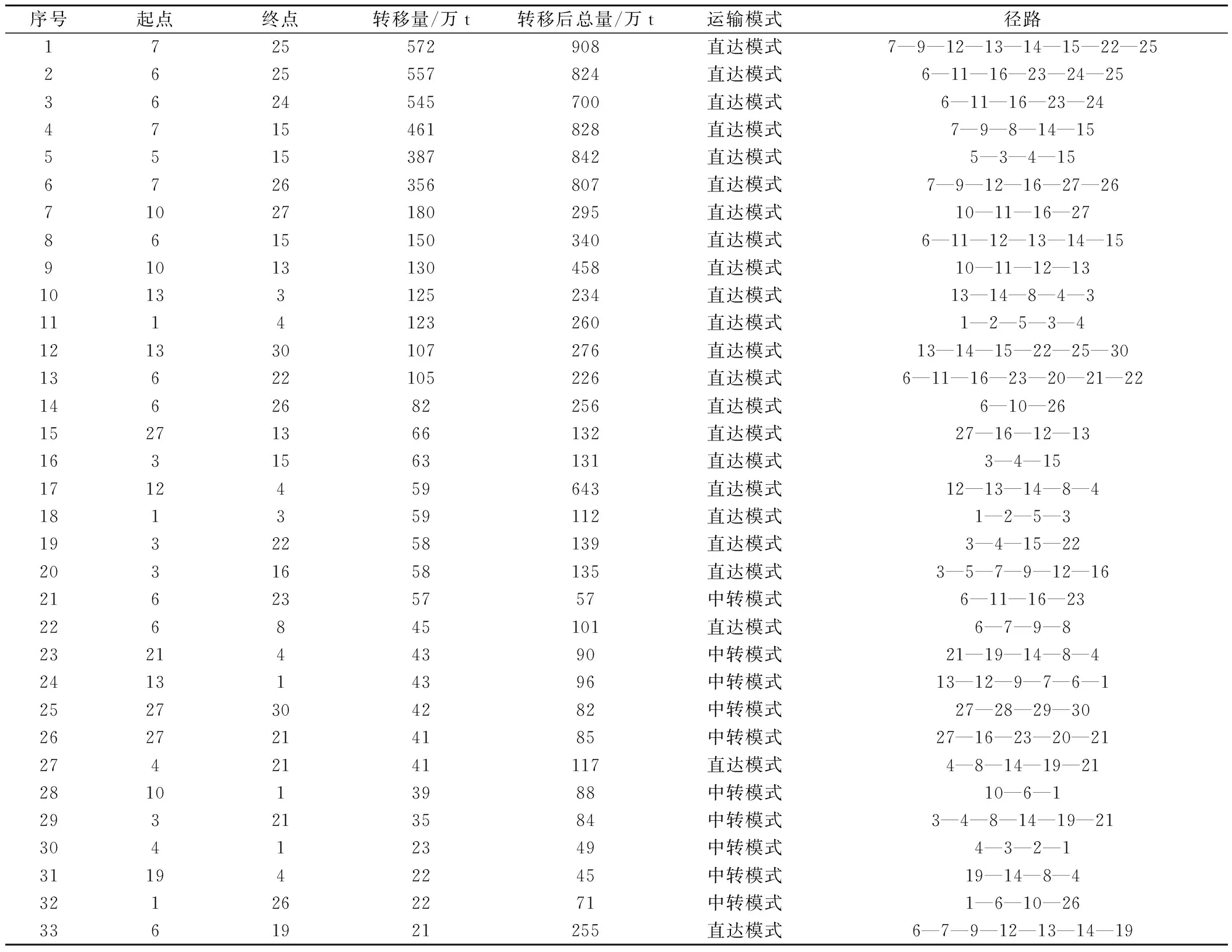
表8 部分OD间公铁货流转移情况

5 结论与展望

本文分析了公铁货流转移与铁路车流径路优化之间相互影响的机理，提出了将两者统筹考虑并进行综合优化的观点。基于该观点构造了以公铁两网综合物流成本最小化为目标的公铁货流转移与铁路车流径路联合优化模型。鉴于铁路货运OD的变化可能影响车流组织模式，模型中设计了辅助0-1决策变量用以根据运量的变化动态决策其适用的车流组织模式，进而根据不同的车流组织规则进行车流径路优化。从而同时实现公铁货流转移优化、车流组织模式判定和铁路车流径路优化。最后设计了数值算例并进行了求解试验，求解结果表明该模型是可行、有效的。由于我国实际铁路网规模庞大，路网节点和区段数量的增加会使决策变量和约束条件的数量明显增多，从而使模型求解的计算复杂性显著提高。所以目前在商业优化软件求解能力有限的情况下，直接应用该模型求解我国全路网规模的问题还比较困难。因此，未来需要进一步研究高效算法以及高性能计算机的应用以解决大规模实际路网的优化问题。