关于函数最值问题的理论探讨与解法示例

李彬彬

[摘  要] 函数最值问题可以全面考查学生的能力，以该类问题为基础开展教学探讨，引导学生掌握解法对于提升学生能力、发展核心素养极为有利. 文章剖析函数最值问题，探讨理论基础，举例探析常用解法.

[关键词] 函数;最值;理论;方法;建议

■问题综述

函数最值问题是数学的一类典型问题，涉及众多数学知识，与生产实际也息息相关. 函数是问题的灵魂所在，其中的最值则是函数的一种重要属性，问题突破需要从函数的性质角度出发来探究，对学生基础知识和数学思维有着一定的要求. 同时该类问题的求解过程需要利用一些思想方法，利用数学思想来构建解题思路，因此解题过程可视为是基础知识、解题方法和数学思想的综合.

分析函数最值问题类型，总体上有以下两个特点：（1）问题的呈现形式主要有三种命题形式，①直接给出函数，求该函数的最值;②在解答问题中作为子问题，需要给出解析过程;③以隐含问题构建，如不等式、存在性问题、几何应用题优化等，解析时需要将其转化为最值问题. （2）问题的变量多变，单一变量较为简单，多变量函数最值问题，虽形式简单，但难以找到突破口，需要进行化归转化.

■突破理论

函数最值问题较为典型，对学生的解析思维有着一定的要求，提升学生问题解析能力需要从三方面入手：（1）深入理解最值概念，从不等式角度加以剖析，把握其中的两个要素，①不等式与函数最值的关联，关注不等式恒成立中的定义域;②关注不等式成立时等号的选取. （2）透视复杂函数，归纳多变量函数最值问题，提升学生发现问题、解析问题的能力. （3）函数最值的概念与其他知识有着紧密的关联，综合性和应用性较强，应强化学生的应用意识和转化意识，深入培养学生的建模能力、數学分析能力，提升学生的核心素养.

函数最值问题的求解需要掌握一定的理论基础，从本质上看就是求函数的最大值和最小值，因此需要深入理解最值定理，定理内容中对函数的区间进行了分类，明确了连续函数和有断点的函数，理解时需要关注有最值的情形，而对于不连续的函数则需要讨论断点处是否有最值，不能一味地照搬连续函数最值问题的解析思路.

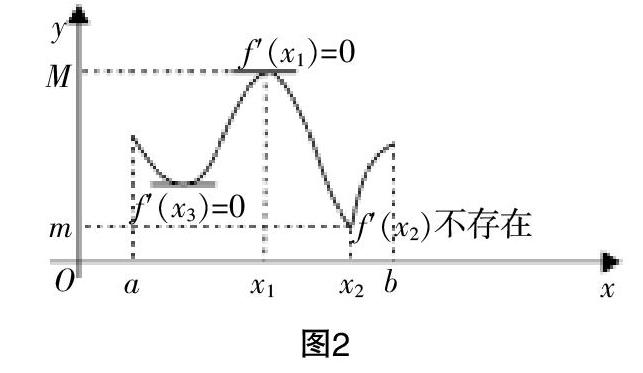
对于函数最值问题，求解时可以结合函数区间上连续与图像曲线连续之间的关联，即“f（x）在区间上连续”？葑“函数图像为连续曲线”. 求函数的最值实则就是求在区间上曲线的最值点，可能的点包括曲线的端点和曲线内部的凸点和凹点. 在解析教学时需要利用直观的图像来展示问题，如图1函数，将其转化为较为简单的直接的问题. 同时引导学生关注问题根本，可以肯定的是：在函数区间上的最值必然也是局部的最大值或最小值，因此在该情形下，函数的极值点就是其最值点;而对于开区间（a，b），其驻点和不可导点就是其极值点，只需要提取函数中的这些特殊点，然后计算特殊点对应的值，并加以比较就可以确定结论. 教学中同样可以借助直观的图像，如图2所示，端点坐标是（a，f（a））和（b，f（b）），驻点坐标为（x■，f（x■））和（x■，f（x■）），而（x■，f（x■））为其不可导点. 若求解f（x）的最值，通过比较上述特殊点位置处的函数值大小就可实现.

从上述分析可以得出如下结论：求解闭区间上连续函数的最值，只需要关注其中的端点、驻点和不可导点. 具体求解可以按照一定的思路方法进行，概括为“求导，找点，计算，比较”八字.

①首先，根据题设条件明确f（x）的区间，求解f′（x）;

②其次，根据导函数f′（x）提取开区间上的特殊位置的点（驻点、不可导点）;

③然后，逐个计算三大类点（端点、驻点、不可导点）处具体的值;

④对比三大类点的函数值，根据值的大小即可确定函数的最大值和最小值.

■方法解读

对于函数最值问题，在掌握基本的解题思路基础上，还需要关注其具体的解题方法，该类问题的解法也较为多样，合理利用可以显著提高解题效率. 解析问题时可采用代数转化法和函数单调性等方法，针对具体的问题需要根据函数的解析式、变量个数、函数曲线、区间特点等来选定方法，下面举例讲解.

1. 配方法

配方法是求解该类问题的有效解法，主要内容是将函数解析式中的某些项分配为一个或多个多项式，从而达到简化问题的效果. 该方法较为简单，容易掌握，对于三角函数最值问题，可以采用配方法对函数解析式进行转化，后续利用正弦或余弦函数的值域来确定原函数的最值;而对于复合性函数，则可以整体上转化为二次函数形式，利用二次函数的性质来解决，如下列问题可用配方法解决.

例1：已知函数y=2x+2-3·4x，如果-1≤x≤0，试求该函数的最值.

解析：上述函数属于复合函数，利用配方法可逐步将问题变为对应的二次函数，具体如下，y=-32x-■■+■，已知-1≤x≤0，则■≤2x≤1. 由二次函数的性质即可得：当2x=1时，取得最小值1;当2x=■时，取得最大值■.

评析：上述函数采用配方法，最终将最值问题变为了二次函数问题，从而借用二次函数的性质确定了最值. 这是由于转化后函数单调性简单明了，可直接确定函数在区间上的变化趋势，问题中最小值的点位于其端点处，而最大值的点位于其驻点处.

2. 单调性法

单调性法，即利用函数的单调性来确定函数在定义域上变化趋势的方法. 求解时可以借用求导的方式来确定函数的单调性，然后根据其单调性直接获得最值点.

例2：已知f（x）=x3-3x+1，试求函数在区间[-3，0]上的最值.

解析：上述为一元三次函数，可以结合求导利用函数单调性法来求解，则有f′（x）=3x2-3，分析可知在[-3，-1）上，f′（x）>0，f（x）在该区间内为增函数;在[-1，0]上，f′（x）≤0，f（x）在该区间内为减函数. 综合分析可知x=-1时f（x）取得最大值，且f（-1）=3，则其最小值在端点处，由于f（-3）=-17< f（0）=1. 综上可知原函数的最大值为3，最小值为-17.

评析：上述求解函数的最值采用了单调性法，而函数的单调性确定使用了求导的方式，其中函数的定义域对函数最值的确定十分重要，解析时需要结合函数单调性和定义域来确定最值点.

3. 换元法

换元法也是求函数最值常用的方法，同样可用于复合性函数，可有效降低思维难度. 该方法指的是在解析时通过引入一个或多个新的变量来替换原函数中的某些变量，从而简化函数. 解析函数最值问题，换元的方式有两类，包括代数换元和三角换元，具体解题时可以根据函数形式来灵活选取.

例3：试求函数y=■的最大值.

解析：该问为涉及三角函数的最值问题，可以对函数进行适当变形，采用换元的方法来简化. 变形可得y=■=（sinx+1）+■，令1+sinx=t，则0

评析：上述函数复合了三角函数，显然采用换元的方法更为有效，将问题转化为了更为简洁的函数. 同时换元过程中重新确定了新函数的定义域，为后续的最值分析提供了条件，解析时需要关注定义域的变化.

■思考建议

函数最值属于综合性问题，在实际教学中需要注重教学重点，注意调动学生参与思考. 如课堂教学应深入探究函数最值问题的根本，将解题步骤和方法作为教学重点，引导学生掌握不同问题的解析方法，提升学生解题思维的灵活性. 课堂教学中应充分激发学生的学习兴趣，尊重学生的主体地位，引导其参与教学讨论，主动思考问题. 同时教学中可适当借助知识框图，帮助学生梳理问题难点、知识脉络、方法核心，用形象的联想来构建类型问题的解题策略.